A Comprehensive Survey of Graph-level Learning

Graphs have a superior ability to represent relational data, like chemical compounds, proteins, and social networks. Hence, graph-level learning, which takes a set of graphs as input, has been applied to many tasks including comparison, regression, classification, and more. Traditional approaches to learning a set of graphs tend to rely on hand-crafted features, such as substructures. But while these methods benefit from good interpretability, they often suffer from computational bottlenecks as they cannot skirt the graph isomorphism problem. Conversely, deep learning has helped graph-level learning adapt to the growing scale of graphs by extracting features automatically and decoding graphs into low-dimensional representations. As a result, these deep graph learning methods have been responsible for many successes. Yet, there is no comprehensive survey that reviews graph-level learning starting with traditional learning and moving through to the deep learning approaches. This article fills this gap and frames the representative algorithms into a systematic taxonomy covering traditional learning, graph-level deep neural networks, graph-level graph neural networks, and graph pooling. To ensure a thoroughly comprehensive survey, the evolutions, interactions, and communications between methods from four different branches of development are also examined. This is followed by a brief review of the benchmark data sets, evaluation metrics, and common downstream applications. The survey concludes with 13 future directions of necessary research that will help to overcome the challenges facing this booming field.

Decompositional Quantum Graph Neural Network

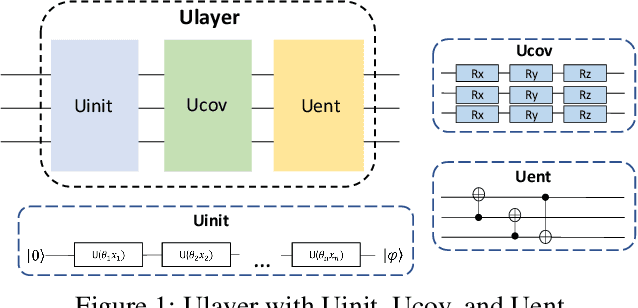
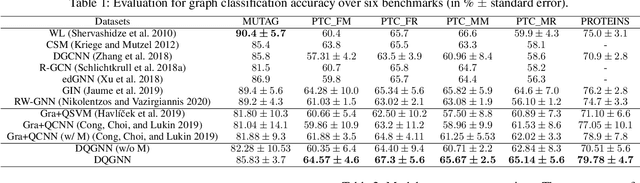
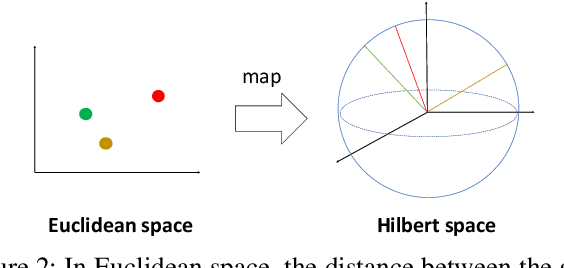
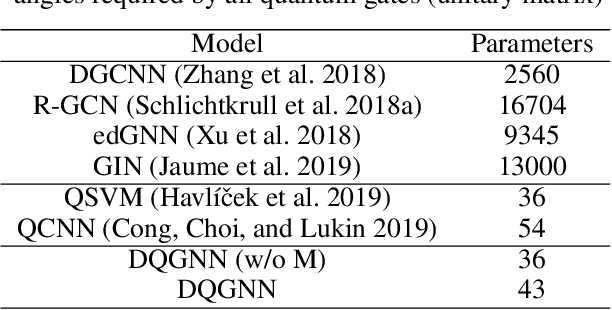
Quantum machine learning is a fast emerging field that aims to tackle machine learning using quantum algorithms and quantum computing. Due to the lack of physical qubits and an effective means to map real-world data from Euclidean space to Hilbert space, most of these methods focus on quantum analogies or process simulations rather than devising concrete architectures based on qubits. In this paper, we propose a novel hybrid quantum-classical algorithm for graph-structured data, which we refer to as the Decompositional Quantum Graph Neural Network (DQGNN). DQGNN implements the GNN theoretical framework using the tensor product and unity matrices representation, which greatly reduces the number of model parameters required. When controlled by a classical computer, DQGNN can accommodate arbitrarily sized graphs by processing substructures from the input graph using a modestly-sized quantum device. The architecture is based on a novel mapping from real-world data to Hilbert space. This mapping maintains the distance relations present in the data and reduces information loss. Experimental results show that the proposed method outperforms competitive state-of-the-art models with only 1.68\% parameters compared to those models.

Region-wise Generative Adversarial ImageInpainting for Large Missing Areas

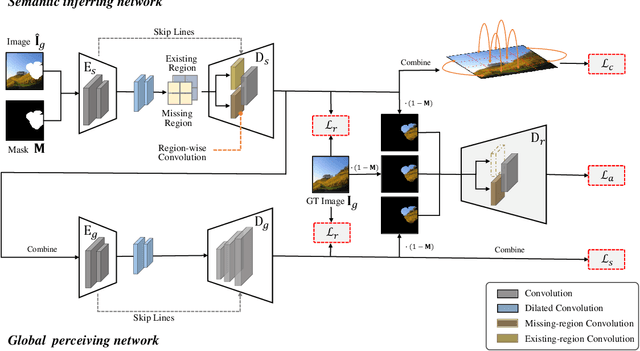
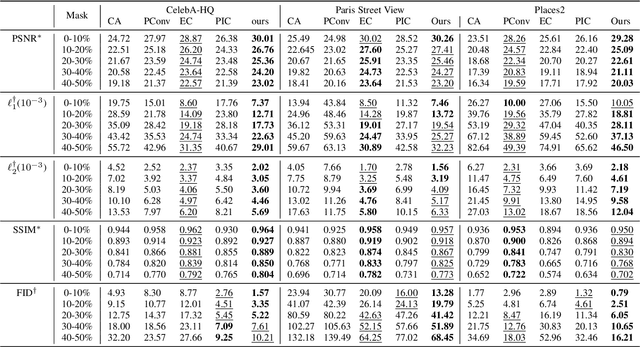
Recently deep neutral networks have achieved promising performance for filling large missing regions in image inpainting tasks. They usually adopted the standard convolutional architecture over the corrupted image, leading to meaningless contents, such as color discrepancy, blur and artifacts. Moreover, most inpainting approaches cannot well handle the large continuous missing area cases. To address these problems, we propose a generic inpainting framework capable of handling with incomplete images on both continuous and discontinuous large missing areas, in an adversarial manner. From which, region-wise convolution is deployed in both generator and discriminator to separately handle with the different regions, namely existing regions and missing ones. Moreover, a correlation loss is introduced to capture the non-local correlations between different patches, and thus guides the generator to obtain more information during inference. With the help of our proposed framework, we can restore semantically reasonable and visually realistic images. Extensive experiments on three widely-used datasets for image inpainting tasks have been conducted, and both qualitative and quantitative experimental results demonstrate that the proposed model significantly outperforms the state-of-the-art approaches, both on the large continuous and discontinuous missing areas.