KC-GenRe: A Knowledge-constrained Generative Re-ranking Method Based on Large Language Models for Knowledge Graph Completion

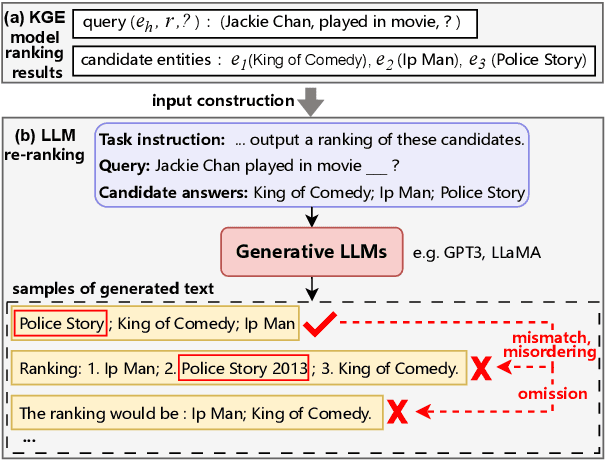
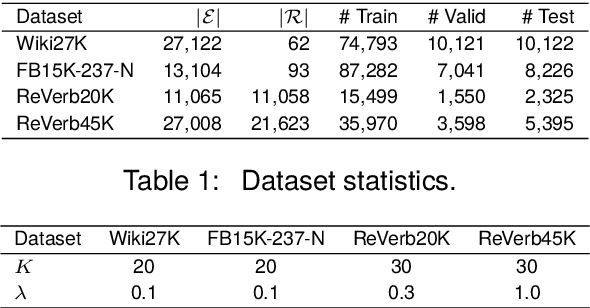
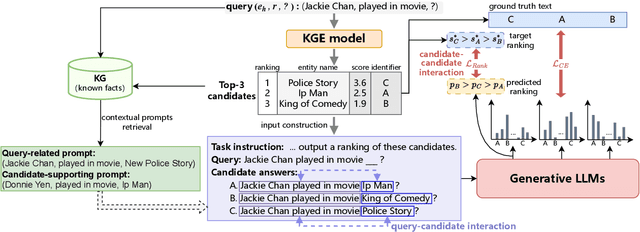
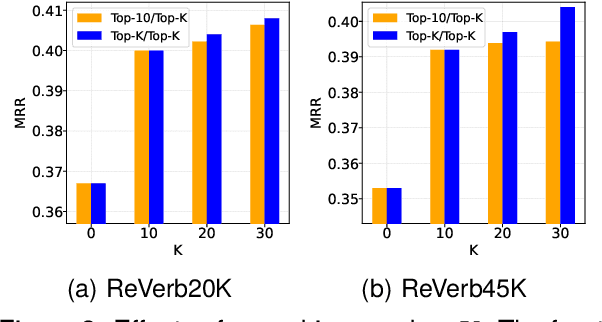
The goal of knowledge graph completion (KGC) is to predict missing facts among entities. Previous methods for KGC re-ranking are mostly built on non-generative language models to obtain the probability of each candidate. Recently, generative large language models (LLMs) have shown outstanding performance on several tasks such as information extraction and dialog systems. Leveraging them for KGC re-ranking is beneficial for leveraging the extensive pre-trained knowledge and powerful generative capabilities. However, it may encounter new problems when accomplishing the task, namely mismatch, misordering and omission. To this end, we introduce KC-GenRe, a knowledge-constrained generative re-ranking method based on LLMs for KGC. To overcome the mismatch issue, we formulate the KGC re-ranking task as a candidate identifier sorting generation problem implemented by generative LLMs. To tackle the misordering issue, we develop a knowledge-guided interactive training method that enhances the identification and ranking of candidates. To address the omission issue, we design a knowledge-augmented constrained inference method that enables contextual prompting and controlled generation, so as to obtain valid rankings. Experimental results show that KG-GenRe achieves state-of-the-art performance on four datasets, with gains of up to 6.7% and 7.7% in the MRR and Hits@1 metric compared to previous methods, and 9.0% and 11.1% compared to that without re-ranking. Extensive analysis demonstrates the effectiveness of components in KG-GenRe.

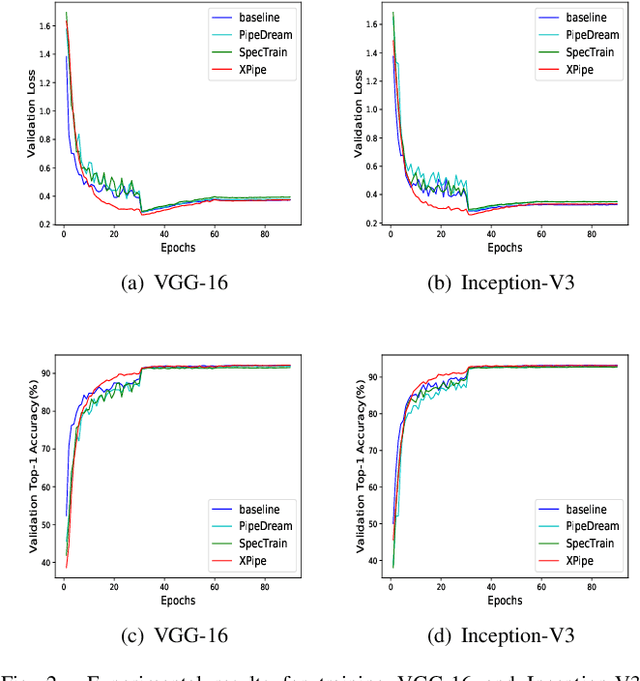
PipeOptim: Ensuring Effective 1F1B Schedule with Optimizer-Dependent Weight Prediction

Asynchronous pipeline model parallelism with a "1F1B" (one forward, one backward) schedule generates little bubble overhead and always provides quite a high throughput. However, the "1F1B" schedule inevitably leads to weight inconsistency and weight staleness issues due to the cross-training of different mini-batches across GPUs. To simultaneously address these two problems, in this paper, we propose an optimizer-dependent weight prediction strategy (a.k.a PipeOptim) for asynchronous pipeline training. The key insight of our proposal is that we employ a weight prediction strategy in the forward pass to ensure that each mini-batch uses consistent and staleness-free weights to compute the forward pass. To be concrete, we first construct the weight prediction scheme based on the update rule of the used optimizer when training the deep neural network models. Then throughout the "1F1B" pipelined training, each mini-batch is mandated to execute weight prediction ahead of the forward pass, subsequently employing the predicted weights to perform the forward pass. As a result, PipeOptim 1) inherits the advantage of the "1F1B" schedule and generates pretty high throughput, and 2) can ensure effective parameter learning regardless of the type of the used optimizer. To verify the effectiveness of our proposal, we conducted extensive experimental evaluations using eight different deep-learning models spanning three machine-learning tasks including image classification, sentiment analysis, and machine translation. The experiment results demonstrate that PipeOptim outperforms the popular pipelined approaches including GPipe, PipeDream, PipeDream-2BW, and SpecTrain. The code of PipeOptim can be accessible at https://github.com/guanleics/PipeOptim.

XPipe: Efficient Pipeline Model Parallelism for Multi-GPU DNN Training

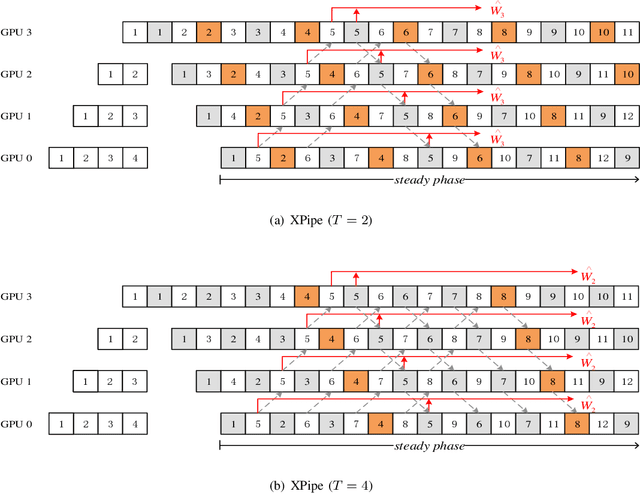
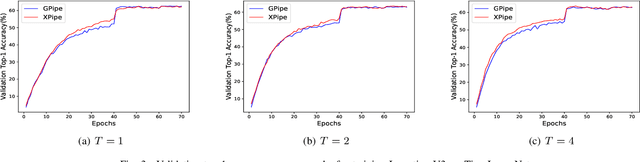
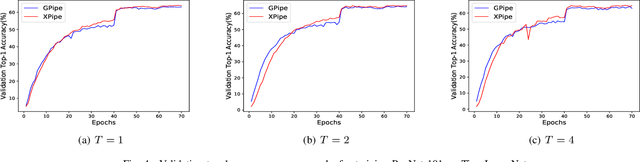
We propose XPipe, an efficient asynchronous pipeline model parallelism approach for multi-GPU DNN training. XPipe is designed to make use of multiple GPUs to concurrently and continuously train different parts of a DNN model. To improve GPU utilization and achieve high throughput, it splits a mini-batch into a set of micro-batches and allows the overlapping of the pipelines of multiple micro-batches, including those belonging to different mini-batches. Most importantly, the novel weight prediction strategy adopted by XPipe enables it to effectively address the weight inconsistency and staleness issues incurred by the asynchronous pipeline parallelism. As a result, XPipe incorporates the advantages of both synchronous and asynchronous pipeline model parallelism approaches. Concretely, it can achieve very comparable (even slightly better) model accuracy as its synchronous counterpart, while obtaining higher throughput than it. Experimental results show that XPipe outperforms other state-of-the-art synchronous and asynchronous model parallelism approaches.

An Efficient ADMM-Based Algorithm to Nonconvex Penalized Support Vector Machines

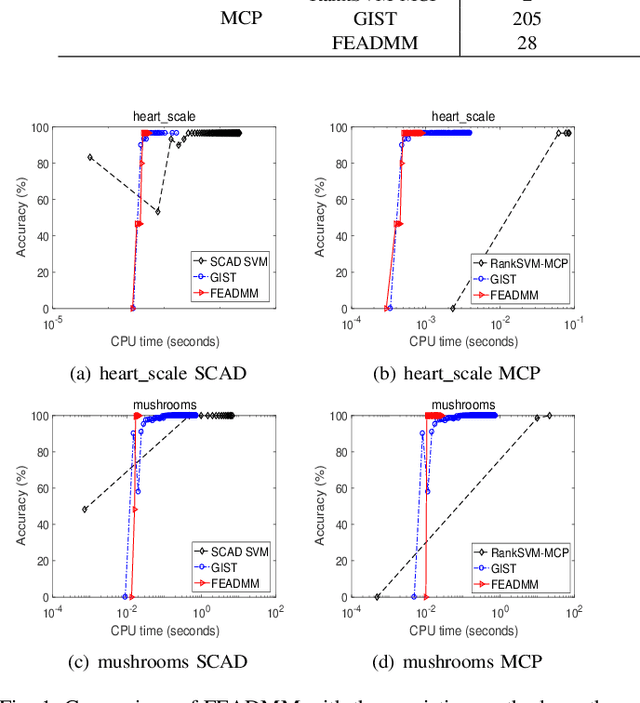
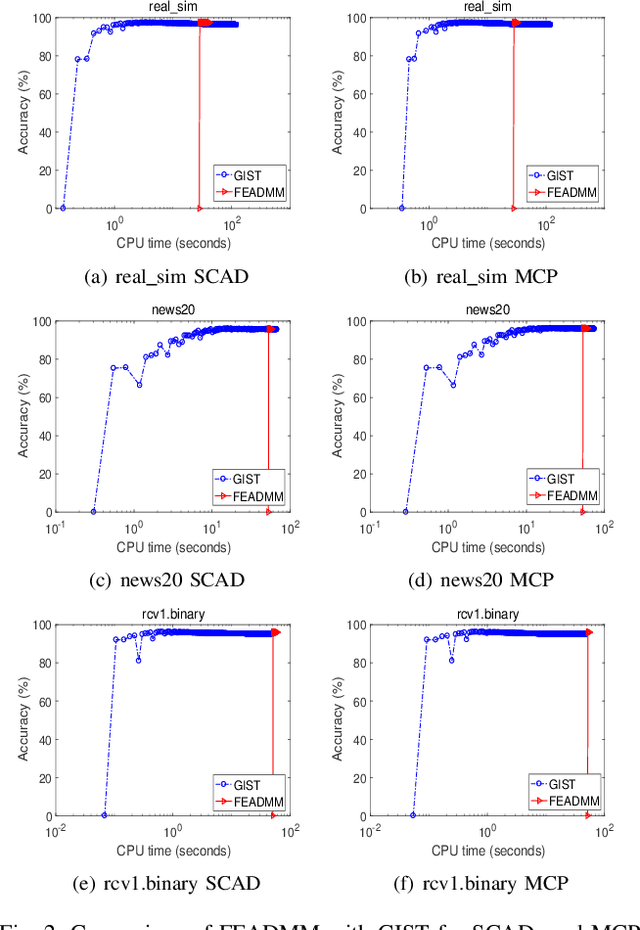
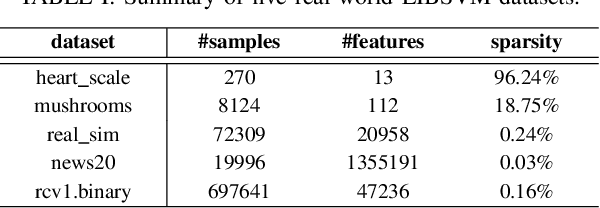
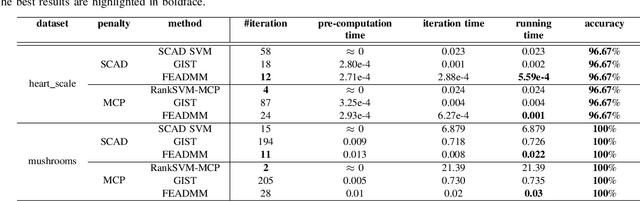
Support vector machines (SVMs) with sparsity-inducing nonconvex penalties have received considerable attentions for the characteristics of automatic classification and variable selection. However, it is quite challenging to solve the nonconvex penalized SVMs due to their nondifferentiability, nonsmoothness and nonconvexity. In this paper, we propose an efficient ADMM-based algorithm to the nonconvex penalized SVMs. The proposed algorithm covers a large class of commonly used nonconvex regularization terms including the smooth clipped absolute deviation (SCAD) penalty, minimax concave penalty (MCP), log-sum penalty (LSP) and capped-$\ell_1$ penalty. The computational complexity analysis shows that the proposed algorithm enjoys low computational cost. Moreover, the convergence of the proposed algorithm is guaranteed. Extensive experimental evaluations on five benchmark datasets demonstrate the superior performance of the proposed algorithm to other three state-of-the-art approaches.

Loss Rank Mining: A General Hard Example Mining Method for Real-time Detectors

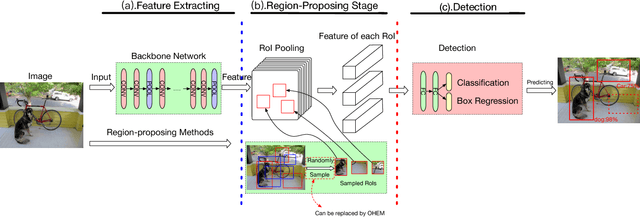
Modern object detectors usually suffer from low accuracy issues, as foregrounds always drown in tons of backgrounds and become hard examples during training. Compared with those proposal-based ones, real-time detectors are in far more serious trouble since they renounce the use of region-proposing stage which is used to filter a majority of backgrounds for achieving real-time rates. Though foregrounds as hard examples are in urgent need of being mined from tons of backgrounds, a considerable number of state-of-the-art real-time detectors, like YOLO series, have yet to profit from existing hard example mining methods, as using these methods need detectors fit series of prerequisites. In this paper, we propose a general hard example mining method named Loss Rank Mining (LRM) to fill the gap. LRM is a general method for real-time detectors, as it utilizes the final feature map which exists in all real-time detectors to mine hard examples. By using LRM, some elements representing easy examples in final feature map are filtered and detectors are forced to concentrate on hard examples during training. Extensive experiments validate the effectiveness of our method. With our method, the improvements of YOLOv2 detector on auto-driving related dataset KITTI and more general dataset PASCAL VOC are over 5% and 2% mAP, respectively. In addition, LRM is the first hard example mining strategy which could fit YOLOv2 perfectly and make it better applied in series of real scenarios where both real-time rates and accurate detection are strongly demanded.

On the Iteration Complexity Analysis of Stochastic Primal-Dual Hybrid Gradient Approach with High Probability

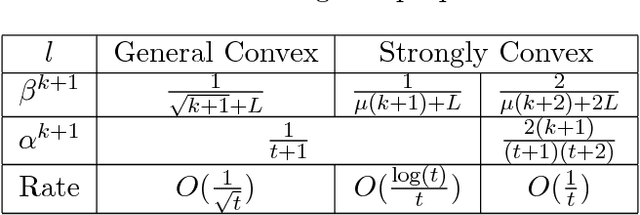
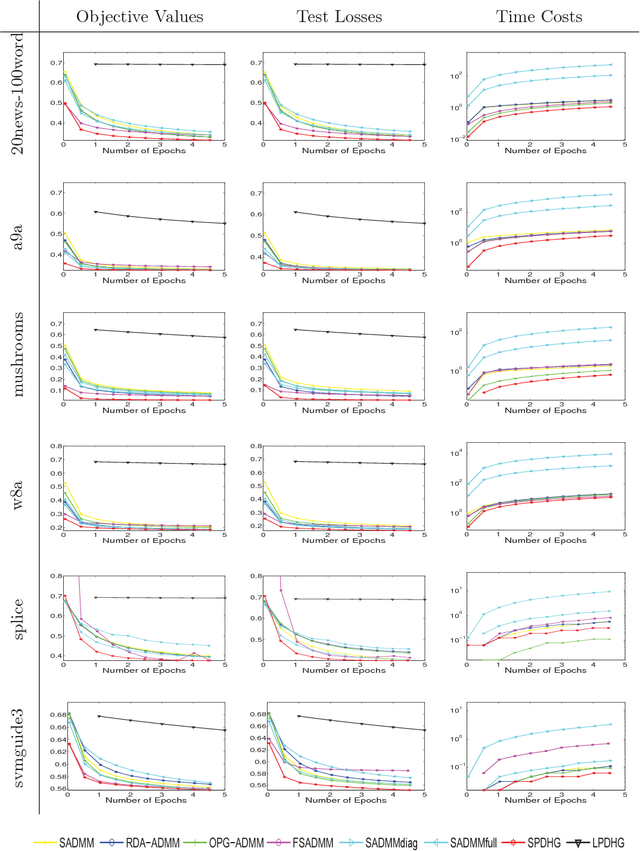
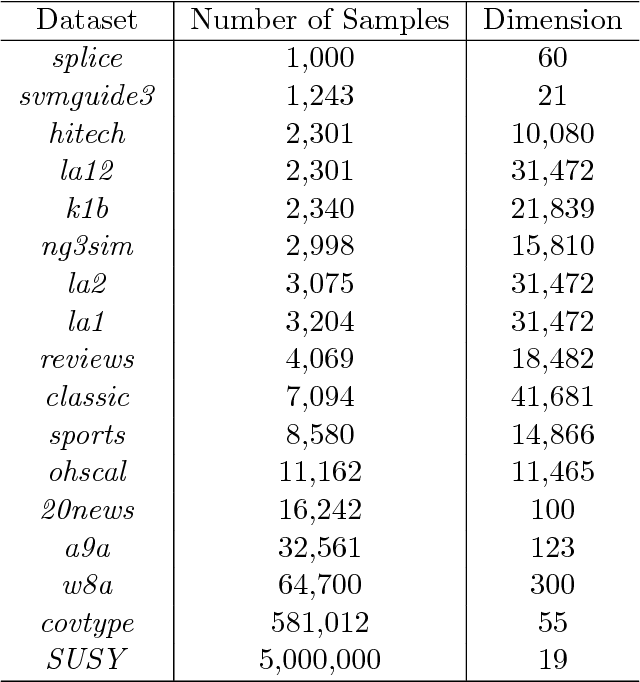
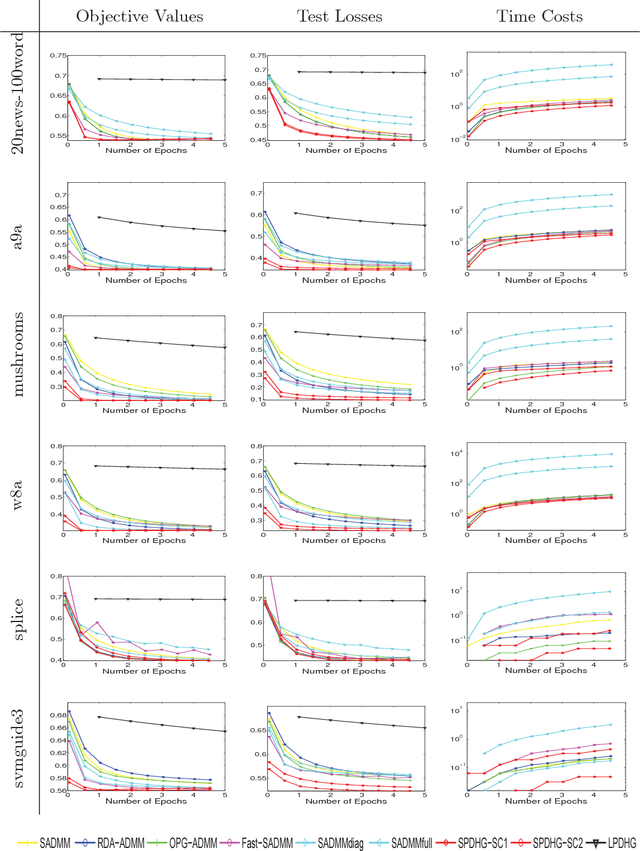
In this paper, we propose a stochastic Primal-Dual Hybrid Gradient (PDHG) approach for solving a wide spectrum of regularized stochastic minimization problems, where the regularization term is composite with a linear function. It has been recognized that solving this kind of problem is challenging since the closed-form solution of the proximal mapping associated with the regularization term is not available due to the imposed linear composition, and the per-iteration cost of computing the full gradient of the expected objective function is extremely high when the number of input data samples is considerably large. Our new approach overcomes these issues by exploring the special structure of the regularization term and sampling a few data points at each iteration. Rather than analyzing the convergence in expectation, we provide the detailed iteration complexity analysis for the cases of both uniformly and non-uniformly averaged iterates with high probability. This strongly supports the good practical performance of the proposed approach. Numerical experiments demonstrate that the efficiency of stochastic PDHG, which outperforms other competing algorithms, as expected by the high-probability convergence analysis.