Self-Recognition in Language Models

A rapidly growing number of applications rely on a small set of closed-source language models (LMs). This dependency might introduce novel security risks if LMs develop self-recognition capabilities. Inspired by human identity verification methods, we propose a novel approach for assessing self-recognition in LMs using model-generated "security questions". Our test can be externally administered to keep track of frontier models as it does not require access to internal model parameters or output probabilities. We use our test to examine self-recognition in ten of the most capable open- and closed-source LMs currently publicly available. Our extensive experiments found no empirical evidence of general or consistent self-recognition in any examined LM. Instead, our results suggest that given a set of alternatives, LMs seek to pick the "best" answer, regardless of its origin. Moreover, we find indications that preferences about which models produce the best answers are consistent across LMs. We additionally uncover novel insights on position bias considerations for LMs in multiple-choice settings.

Evaluating Language Model Agency through Negotiations

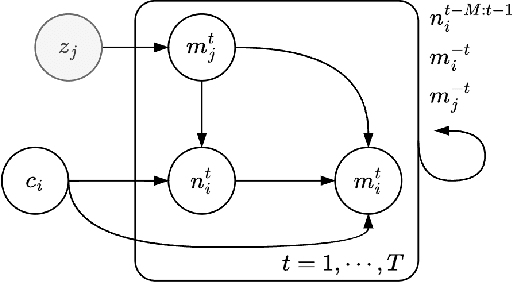
Companies, organizations, and governments increasingly exploit Language Models' (LM) remarkable capability to display agent-like behavior. As LMs are adopted to perform tasks with growing autonomy, there exists an urgent need for reliable and scalable evaluation benchmarks. Current, predominantly static LM benchmarks are ill-suited to evaluate such dynamic applications. Thus, we propose jointly evaluating LM performance and alignment through the lenses of negotiation games. We argue that this common task better reflects real-world deployment conditions while offering insights into LMs' decision-making processes. Crucially, negotiation games allow us to study multi-turn, and cross-model interactions, modulate complexity, and side-step accidental data leakage in evaluation. We report results for six publicly accessible LMs from several major providers on a variety of negotiation games, evaluating both self-play and cross-play performance. Noteworthy findings include: (i) open-source models are currently unable to complete these tasks; (ii) cooperative bargaining games prove challenging; and (iii) the most powerful models do not always "win".

Increasing Expressivity of a Hyperspherical VAE

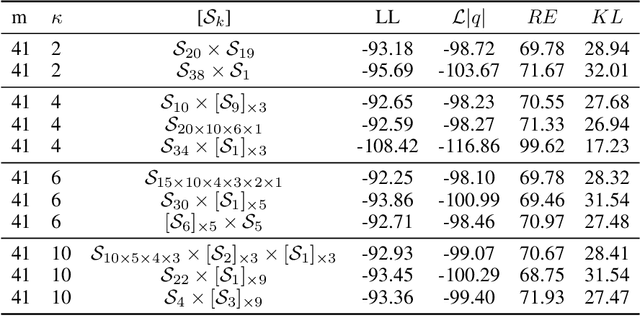
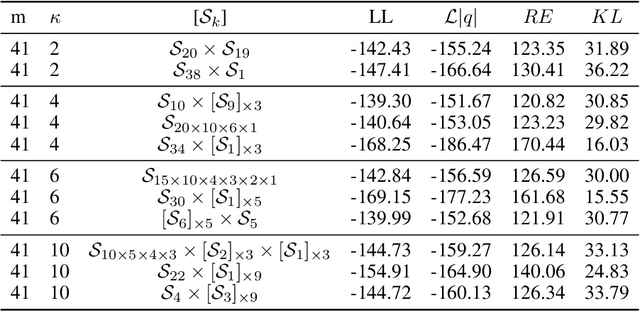
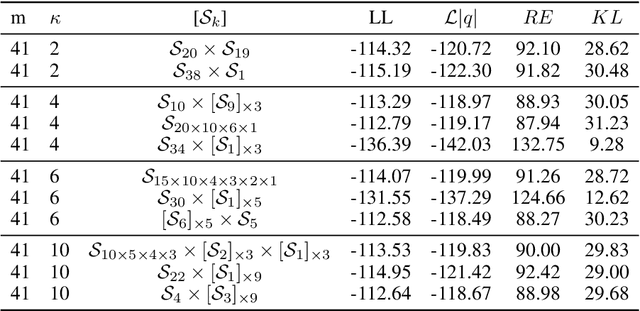
Learning suitable latent representations for observed, high-dimensional data is an important research topic underlying many recent advances in machine learning. While traditionally the Gaussian normal distribution has been the go-to latent parameterization, recently a variety of works have successfully proposed the use of manifold-valued latents. In one such work (Davidson et al., 2018), the authors empirically show the potential benefits of using a hyperspherical von Mises-Fisher (vMF) distribution in low dimensionality. However, due to the unique distributional form of the vMF, expressivity in higher dimensional space is limited as a result of its scalar concentration parameter leading to a 'hyperspherical bottleneck'. In this work we propose to extend the usability of hyperspherical parameterizations to higher dimensions using a product-space instead, showing improved results on a selection of image datasets.

Reparameterizing Distributions on Lie Groups

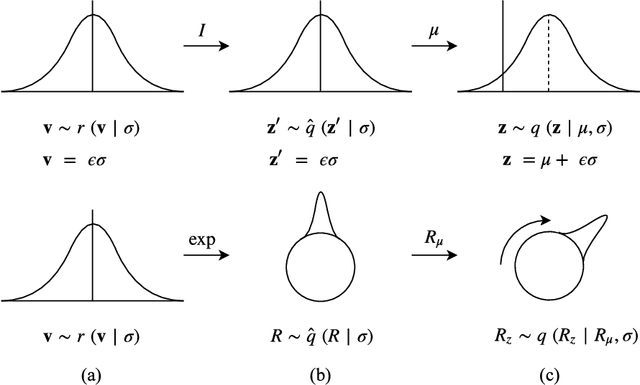
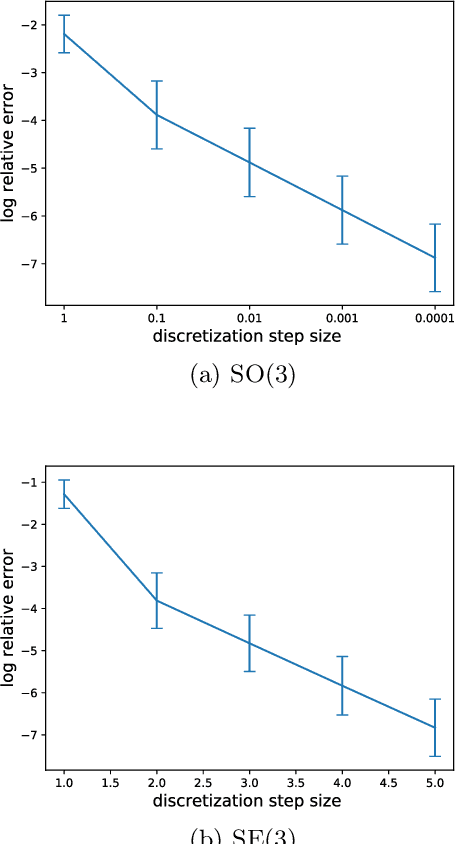
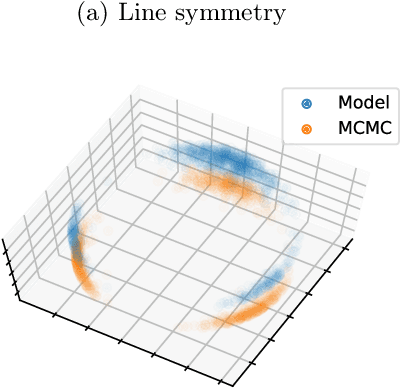
Reparameterizable densities are an important way to learn probability distributions in a deep learning setting. For many distributions it is possible to create low-variance gradient estimators by utilizing a `reparameterization trick'. Due to the absence of a general reparameterization trick, much research has recently been devoted to extend the number of reparameterizable distributional families. Unfortunately, this research has primarily focused on distributions defined in Euclidean space, ruling out the usage of one of the most influential class of spaces with non-trivial topologies: Lie groups. In this work we define a general framework to create reparameterizable densities on arbitrary Lie groups, and provide a detailed practitioners guide to further the ease of usage. We demonstrate how to create complex and multimodal distributions on the well known oriented group of 3D rotations, $\operatorname{SO}(3)$, using normalizing flows. Our experiments on applying such distributions in a Bayesian setting for pose estimation on objects with discrete and continuous symmetries, showcase their necessity in achieving realistic uncertainty estimates.

Hyperspherical Variational Auto-Encoders

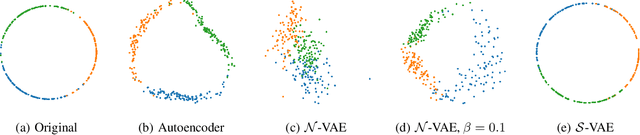
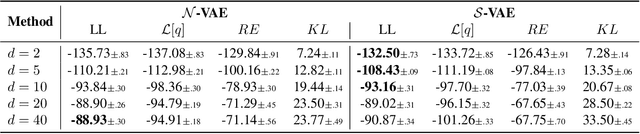
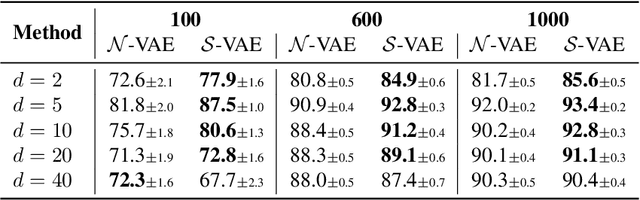
The Variational Auto-Encoder (VAE) is one of the most used unsupervised machine learning models. But although the default choice of a Gaussian distribution for both the prior and posterior represents a mathematically convenient distribution often leading to competitive results, we show that this parameterization fails to model data with a latent hyperspherical structure. To address this issue we propose using a von Mises-Fisher (vMF) distribution instead, leading to a hyperspherical latent space. Through a series of experiments we show how such a hyperspherical VAE, or $\mathcal{S}$-VAE, is more suitable for capturing data with a hyperspherical latent structure, while outperforming a normal, $\mathcal{N}$-VAE, in low dimensions on other data types.

Explorations in Homeomorphic Variational Auto-Encoding

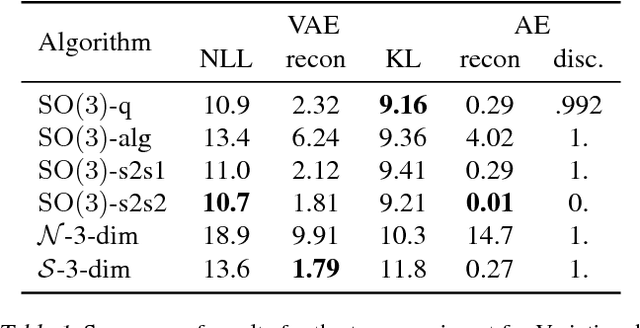
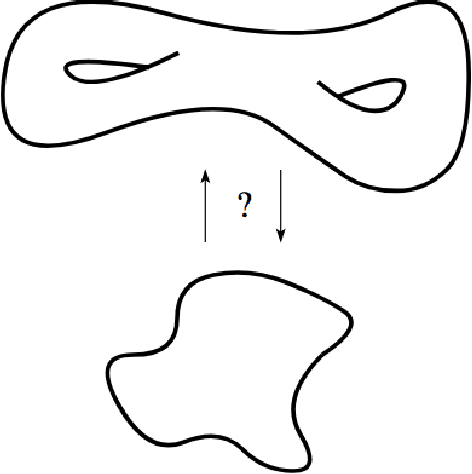
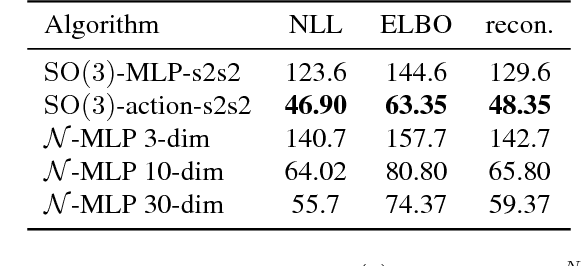
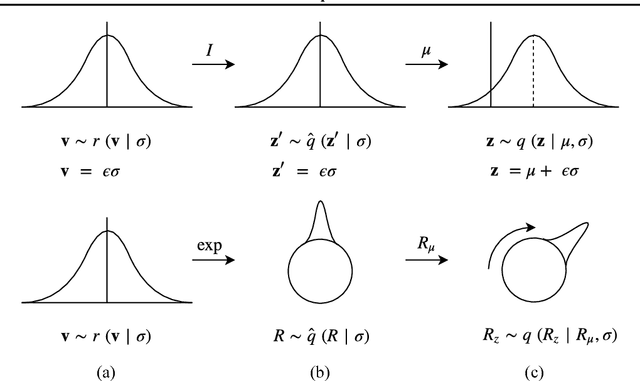
The manifold hypothesis states that many kinds of high-dimensional data are concentrated near a low-dimensional manifold. If the topology of this data manifold is non-trivial, a continuous encoder network cannot embed it in a one-to-one manner without creating holes of low density in the latent space. This is at odds with the Gaussian prior assumption typically made in Variational Auto-Encoders (VAEs), because the density of a Gaussian concentrates near a blob-like manifold. In this paper we investigate the use of manifold-valued latent variables. Specifically, we focus on the important case of continuously differentiable symmetry groups (Lie groups), such as the group of 3D rotations $\operatorname{SO}(3)$. We show how a VAE with $\operatorname{SO}(3)$-valued latent variables can be constructed, by extending the reparameterization trick to compact connected Lie groups. Our experiments show that choosing manifold-valued latent variables that match the topology of the latent data manifold, is crucial to preserve the topological structure and learn a well-behaved latent space.