Unified Policy Value Decomposition for Rapid Adaptation

Rapid adaptation in complex control systems remains a central challenge in reinforcement learning. We introduce a framework in which policy and value functions share a low-dimensional coefficient vector - a goal embedding - that captures task identity and enables immediate adaptation to novel tasks without retraining representations. During pretraining, we jointly learn structured value bases and compatible policy bases through a bilinear actor-critic decomposition. The critic factorizes as Q = sum_k G_k(g) y_k(s,a), where G_k(g) is a goal-conditioned coefficient vector and y_k(s,a) are learned value basis functions. This multiplicative gating - where a context signal scales a set of state-dependent bases - is reminiscent of gain modulation observed in Layer 5 pyramidal neurons, where top-down inputs modulate the gain of sensory-driven responses without altering their tuning. Building on Successor Features, we extend the decomposition to the actor, which composes a set of primitive policies weighted by the same coefficients G_k(g). At test time the bases are frozen and G_k(g) is estimated zero-shot via a single forward pass, enabling immediate adaptation to novel tasks without any gradient update. We train a Soft Actor-Critic agent on the MuJoCo Ant environment under a multi-directional locomotion objective, requiring the agent to walk in eight directions specified as continuous goal vectors. The bilinear structure allows each policy head to specialize to a subset of directions, while the shared coefficient layer generalizes across them, accommodating novel directions by interpolating in goal embedding space. Our results suggest that shared low-dimensional goal embeddings offer a general mechanism for rapid, structured adaptation in high-dimensional control, and highlight a potentially biologically plausible principle for efficient transfer in complex reinforcement learning systems.

Neural Ordinary Differential Equations on Manifolds

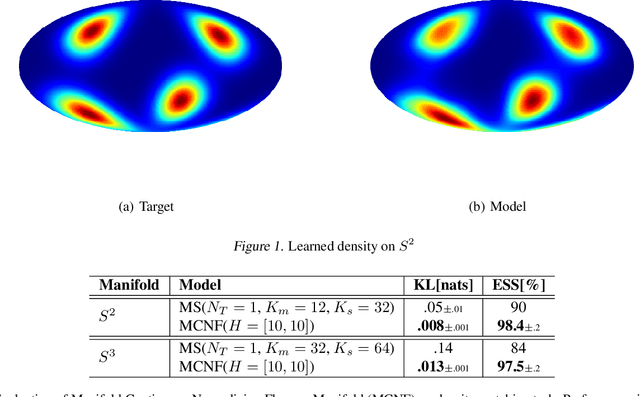
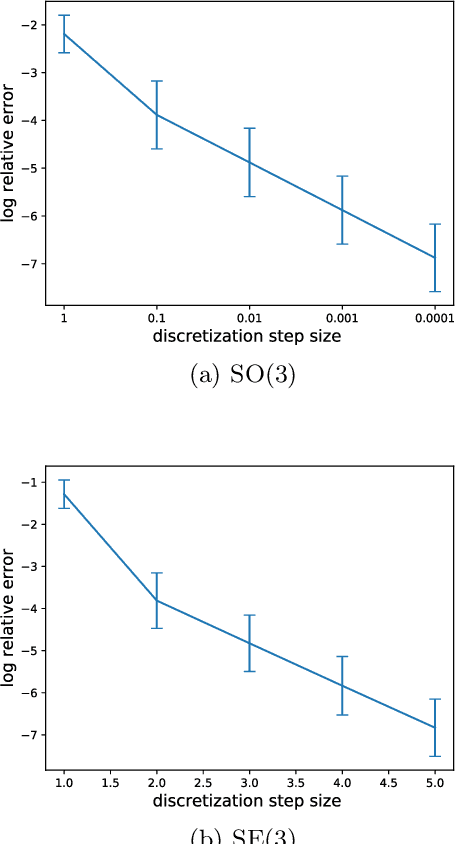
Normalizing flows are a powerful technique for obtaining reparameterizable samples from complex multimodal distributions. Unfortunately current approaches fall short when the underlying space has a non trivial topology, and are only available for the most basic geometries. Recently normalizing flows in Euclidean space based on Neural ODEs show great promise, yet suffer the same limitations. Using ideas from differential geometry and geometric control theory, we describe how neural ODEs can be extended to smooth manifolds. We show how vector fields provide a general framework for parameterizing a flexible class of invertible mapping on these spaces and we illustrate how gradient based learning can be performed. As a result we define a general methodology for building normalizing flows on manifolds.

Reparameterizing Distributions on Lie Groups

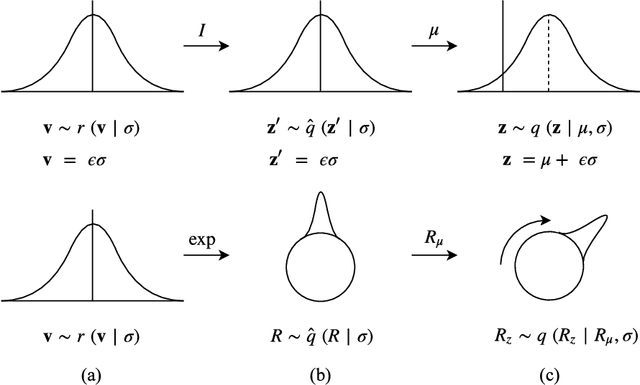
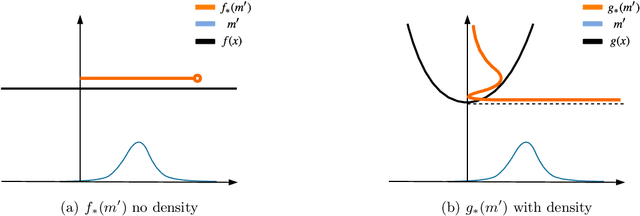
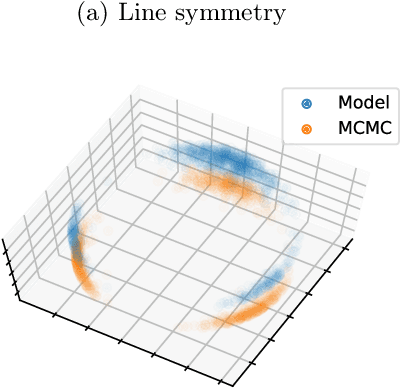
Reparameterizable densities are an important way to learn probability distributions in a deep learning setting. For many distributions it is possible to create low-variance gradient estimators by utilizing a `reparameterization trick'. Due to the absence of a general reparameterization trick, much research has recently been devoted to extend the number of reparameterizable distributional families. Unfortunately, this research has primarily focused on distributions defined in Euclidean space, ruling out the usage of one of the most influential class of spaces with non-trivial topologies: Lie groups. In this work we define a general framework to create reparameterizable densities on arbitrary Lie groups, and provide a detailed practitioners guide to further the ease of usage. We demonstrate how to create complex and multimodal distributions on the well known oriented group of 3D rotations, $\operatorname{SO}(3)$, using normalizing flows. Our experiments on applying such distributions in a Bayesian setting for pose estimation on objects with discrete and continuous symmetries, showcase their necessity in achieving realistic uncertainty estimates.

Topological Constraints on Homeomorphic Auto-Encoding

When doing representation learning on data that lives on a known non-trivial manifold embedded in high dimensional space, it is natural to desire the encoder to be homeomorphic when restricted to the manifold, so that it is bijective and continuous with a continuous inverse. Using topological arguments, we show that when the manifold is non-trivial, the encoder must be globally discontinuous and propose a universal, albeit impractical, construction. In addition, we derive necessary constraints which need to be satisfied when designing manifold-specific practical encoders. These are used to analyse candidates for a homeomorphic encoder for the manifold of 3D rotations $SO(3)$.

Hyperspherical Variational Auto-Encoders

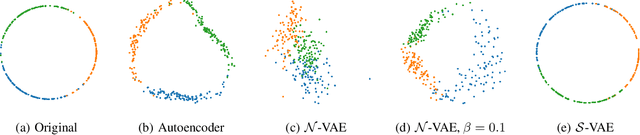
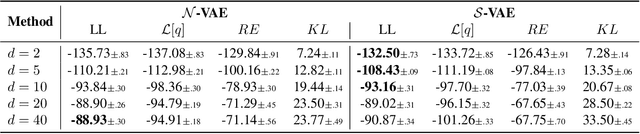
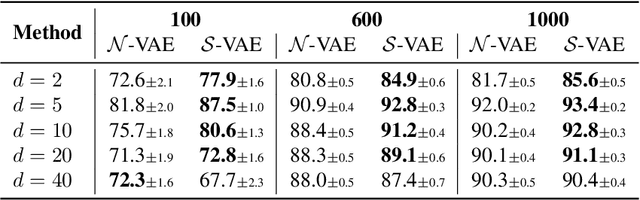
The Variational Auto-Encoder (VAE) is one of the most used unsupervised machine learning models. But although the default choice of a Gaussian distribution for both the prior and posterior represents a mathematically convenient distribution often leading to competitive results, we show that this parameterization fails to model data with a latent hyperspherical structure. To address this issue we propose using a von Mises-Fisher (vMF) distribution instead, leading to a hyperspherical latent space. Through a series of experiments we show how such a hyperspherical VAE, or $\mathcal{S}$-VAE, is more suitable for capturing data with a hyperspherical latent structure, while outperforming a normal, $\mathcal{N}$-VAE, in low dimensions on other data types.

Explorations in Homeomorphic Variational Auto-Encoding

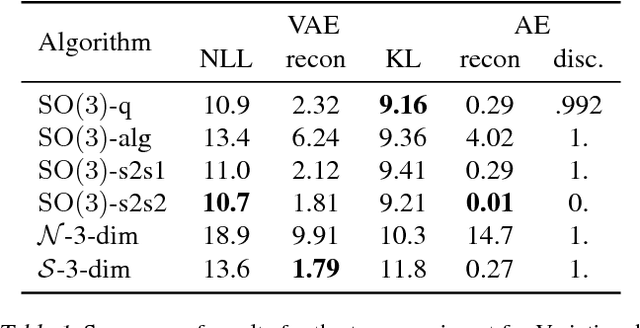
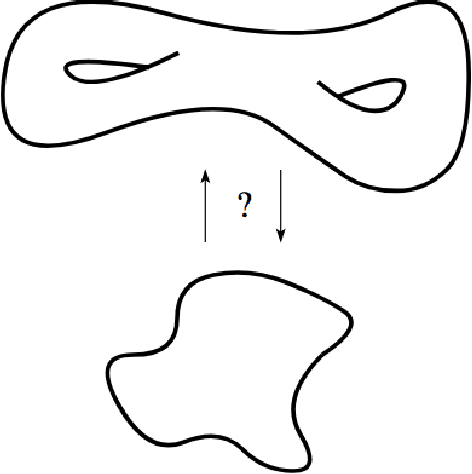
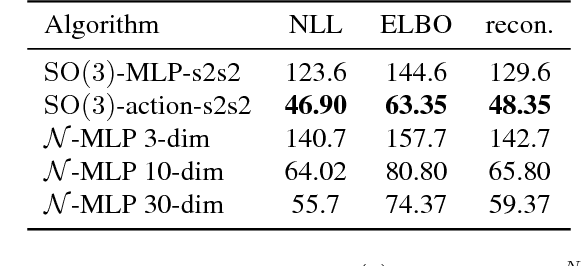
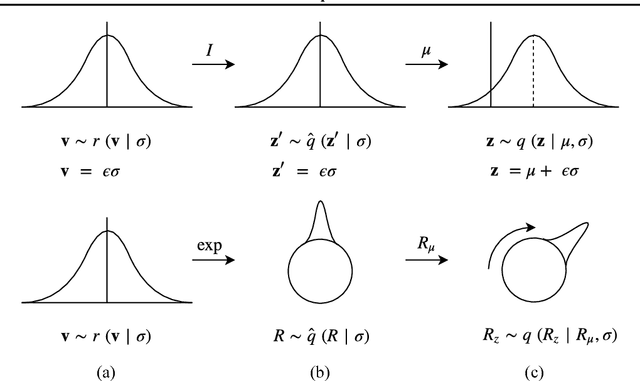
The manifold hypothesis states that many kinds of high-dimensional data are concentrated near a low-dimensional manifold. If the topology of this data manifold is non-trivial, a continuous encoder network cannot embed it in a one-to-one manner without creating holes of low density in the latent space. This is at odds with the Gaussian prior assumption typically made in Variational Auto-Encoders (VAEs), because the density of a Gaussian concentrates near a blob-like manifold. In this paper we investigate the use of manifold-valued latent variables. Specifically, we focus on the important case of continuously differentiable symmetry groups (Lie groups), such as the group of 3D rotations $\operatorname{SO}(3)$. We show how a VAE with $\operatorname{SO}(3)$-valued latent variables can be constructed, by extending the reparameterization trick to compact connected Lie groups. Our experiments show that choosing manifold-valued latent variables that match the topology of the latent data manifold, is crucial to preserve the topological structure and learn a well-behaved latent space.