Topological Constraints on Homeomorphic Auto-Encoding
Paper and Code
Dec 27, 2018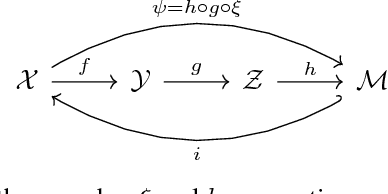
When doing representation learning on data that lives on a known non-trivial manifold embedded in high dimensional space, it is natural to desire the encoder to be homeomorphic when restricted to the manifold, so that it is bijective and continuous with a continuous inverse. Using topological arguments, we show that when the manifold is non-trivial, the encoder must be globally discontinuous and propose a universal, albeit impractical, construction. In addition, we derive necessary constraints which need to be satisfied when designing manifold-specific practical encoders. These are used to analyse candidates for a homeomorphic encoder for the manifold of 3D rotations $SO(3)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge