Increasing Expressivity of a Hyperspherical VAE
Paper and Code
Oct 07, 2019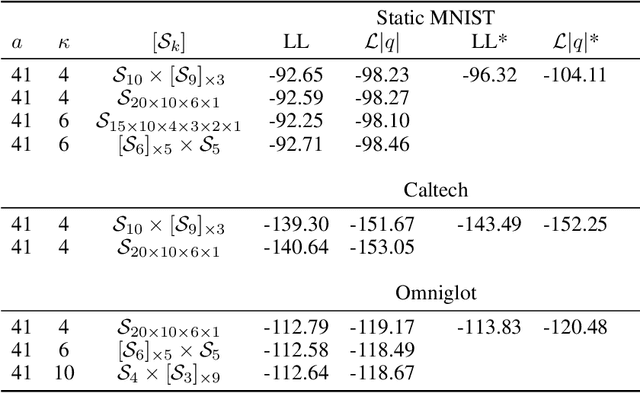
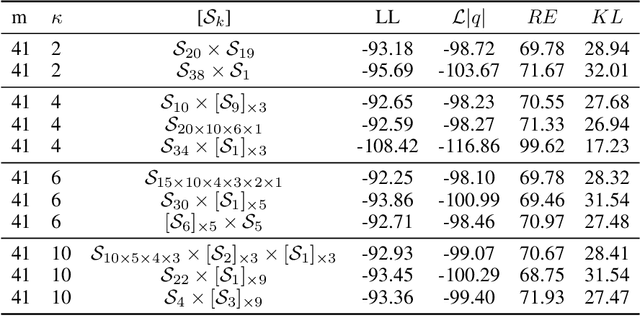
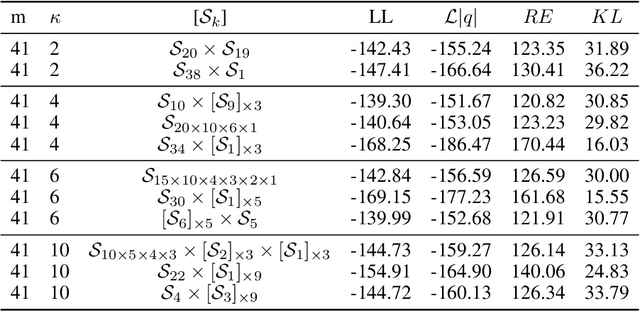
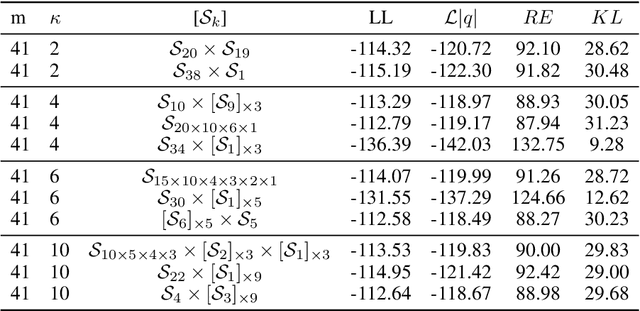
Learning suitable latent representations for observed, high-dimensional data is an important research topic underlying many recent advances in machine learning. While traditionally the Gaussian normal distribution has been the go-to latent parameterization, recently a variety of works have successfully proposed the use of manifold-valued latents. In one such work (Davidson et al., 2018), the authors empirically show the potential benefits of using a hyperspherical von Mises-Fisher (vMF) distribution in low dimensionality. However, due to the unique distributional form of the vMF, expressivity in higher dimensional space is limited as a result of its scalar concentration parameter leading to a 'hyperspherical bottleneck'. In this work we propose to extend the usability of hyperspherical parameterizations to higher dimensions using a product-space instead, showing improved results on a selection of image datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge