Siyang Gao
Bring Reason to Vision: Understanding Perception and Reasoning through Model Merging
May 08, 2025Abstract:Vision-Language Models (VLMs) combine visual perception with the general capabilities, such as reasoning, of Large Language Models (LLMs). However, the mechanisms by which these two abilities can be combined and contribute remain poorly understood. In this work, we explore to compose perception and reasoning through model merging that connects parameters of different models. Unlike previous works that often focus on merging models of the same kind, we propose merging models across modalities, enabling the incorporation of the reasoning capabilities of LLMs into VLMs. Through extensive experiments, we demonstrate that model merging offers a successful pathway to transfer reasoning abilities from LLMs to VLMs in a training-free manner. Moreover, we utilize the merged models to understand the internal mechanism of perception and reasoning and how merging affects it. We find that perception capabilities are predominantly encoded in the early layers of the model, whereas reasoning is largely facilitated by the middle-to-late layers. After merging, we observe that all layers begin to contribute to reasoning, whereas the distribution of perception abilities across layers remains largely unchanged. These observations shed light on the potential of model merging as a tool for multimodal integration and interpretation.
Why Is Spatial Reasoning Hard for VLMs? An Attention Mechanism Perspective on Focus Areas
Mar 04, 2025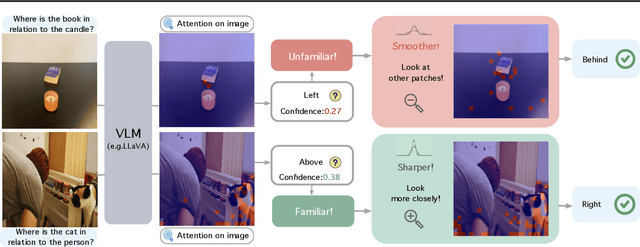


Abstract:Large Vision Language Models (VLMs) have long struggled with spatial reasoning tasks. Surprisingly, even simple spatial reasoning tasks, such as recognizing "under" or "behind" relationships between only two objects, pose significant challenges for current VLMs. In this work, we study the spatial reasoning challenge from the lens of mechanistic interpretability, diving into the model's internal states to examine the interactions between image and text tokens. By tracing attention distribution over the image through out intermediate layers, we observe that successful spatial reasoning correlates strongly with the model's ability to align its attention distribution with actual object locations, particularly differing between familiar and unfamiliar spatial relationships. Motivated by these findings, we propose ADAPTVIS based on inference-time confidence scores to sharpen the attention on highly relevant regions when confident, while smoothing and broadening the attention window to consider a wider context when confidence is lower. This training-free decoding method shows significant improvement (e.g., up to a 50 absolute point improvement) on spatial reasoning benchmarks such as WhatsUp and VSR with negligible cost. We make code and data publicly available for research purposes at https://github.com/shiqichen17/AdaptVis.
Stochastically Constrained Best Arm Identification with Thompson Sampling
Jan 07, 2025Abstract:We consider the problem of the best arm identification in the presence of stochastic constraints, where there is a finite number of arms associated with multiple performance measures. The goal is to identify the arm that optimizes the objective measure subject to constraints on the remaining measures. We will explore the popular idea of Thompson sampling (TS) as a means to solve it. To the best of our knowledge, it is the first attempt to extend TS to this problem. We will design a TS-based sampling algorithm, establish its asymptotic optimality in the rate of posterior convergence, and demonstrate its superior performance using numerical examples.
Image-of-Thought Prompting for Visual Reasoning Refinement in Multimodal Large Language Models
May 22, 2024



Abstract:Recent advancements in Chain-of-Thought (CoT) and related rationale-based works have significantly improved the performance of Large Language Models (LLMs) in complex reasoning tasks. With the evolution of Multimodal Large Language Models (MLLMs), enhancing their capability to tackle complex multimodal reasoning problems is a crucial frontier. However, incorporating multimodal rationales in CoT has yet to be thoroughly investigated. We propose the Image-of-Thought (IoT) prompting method, which helps MLLMs to extract visual rationales step-by-step. Specifically, IoT prompting can automatically design critical visual information extraction operations based on the input images and questions. Each step of visual information refinement identifies specific visual rationales that support answers to complex visual reasoning questions. Beyond the textual CoT, IoT simultaneously utilizes visual and textual rationales to help MLLMs understand complex multimodal information. IoT prompting has improved zero-shot visual reasoning performance across various visual understanding tasks in different MLLMs. Moreover, the step-by-step visual feature explanations generated by IoT prompting elucidate the visual reasoning process, aiding in analyzing the cognitive processes of large multimodal models
In-Context Sharpness as Alerts: An Inner Representation Perspective for Hallucination Mitigation
Mar 12, 2024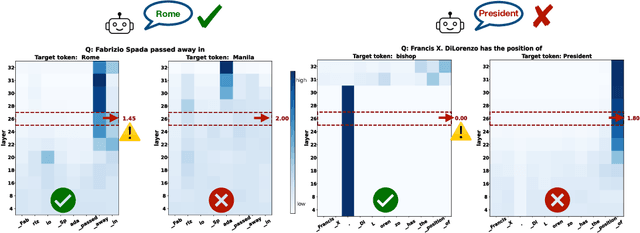
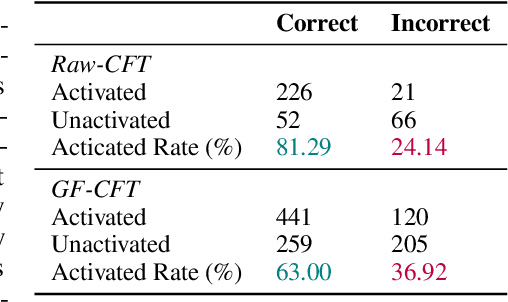
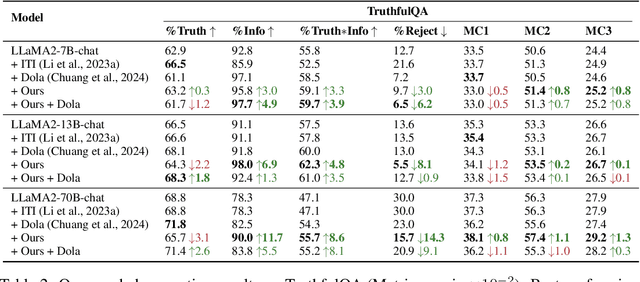
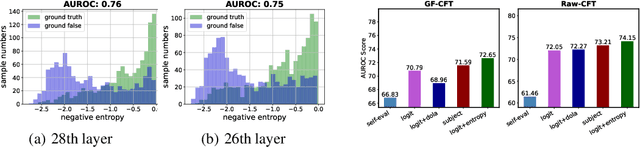
Abstract:Large language models (LLMs) frequently hallucinate and produce factual errors, yet our understanding of why they make these errors remains limited. In this study, we delve into the underlying mechanisms of LLM hallucinations from the perspective of inner representations, and discover a salient pattern associated with hallucinations: correct generations tend to have sharper context activations in the hidden states of the in-context tokens, compared to the incorrect ones. Leveraging this insight, we propose an entropy-based metric to quantify the ``sharpness'' among the in-context hidden states and incorporate it into the decoding process to formulate a constrained decoding approach. Experiments on various knowledge-seeking and hallucination benchmarks demonstrate our approach's consistent effectiveness, for example, achieving up to an 8.6 point improvement on TruthfulQA. We believe this study can improve our understanding of hallucinations and serve as a practical solution for hallucination mitigation.
FELM: Benchmarking Factuality Evaluation of Large Language Models
Oct 01, 2023Abstract:Assessing factuality of text generated by large language models (LLMs) is an emerging yet crucial research area, aimed at alerting users to potential errors and guiding the development of more reliable LLMs. Nonetheless, the evaluators assessing factuality necessitate suitable evaluation themselves to gauge progress and foster advancements. This direction remains under-explored, resulting in substantial impediments to the progress of factuality evaluators. To mitigate this issue, we introduce a benchmark for Factuality Evaluation of large Language Models, referred to as felm. In this benchmark, we collect responses generated from LLMs and annotate factuality labels in a fine-grained manner. Contrary to previous studies that primarily concentrate on the factuality of world knowledge (e.g.~information from Wikipedia), felm focuses on factuality across diverse domains, spanning from world knowledge to math and reasoning. Our annotation is based on text segments, which can help pinpoint specific factual errors. The factuality annotations are further supplemented by predefined error types and reference links that either support or contradict the statement. In our experiments, we investigate the performance of several LLM-based factuality evaluators on felm, including both vanilla LLMs and those augmented with retrieval mechanisms and chain-of-thought processes. Our findings reveal that while retrieval aids factuality evaluation, current LLMs are far from satisfactory to faithfully detect factual errors.
Evaluating Factual Consistency of Summaries with Large Language Models
May 23, 2023



Abstract:Detecting factual errors in summaries has been an important and challenging subject in summarization research. Inspired by the emergent ability of large language models (LLMs), we explore evaluating factual consistency of summaries by directly prompting LLMs. We present a comprehensive empirical study to assess the ability of LLMs as factual consistency evaluators, which consists of (1) analyzing different LLMs such as the GPT model series and Flan-T5; (2) investigating a variety of prompting methods including vanilla prompting, chain-of-thought prompting, and a sentence-by-sentence prompting method to tackle long summaries; and (3) evaluating on diverse summaries generated by multiple summarization systems, ranging from pre-transformer methods to SOTA pretrained models. Our experiments demonstrate that prompting LLMs is able to outperform the previous best factuality systems in all settings, by up to 12.2 absolute points in terms of the binary classification accuracy on inconsistency detection.
Convergence Rate Analysis for Optimal Computing Budget Allocation Algorithms
Nov 29, 2022Abstract:Ordinal optimization (OO) is a widely-studied technique for optimizing discrete-event dynamic systems (DEDS). It evaluates the performance of the system designs in a finite set by sampling and aims to correctly make ordinal comparison of the designs. A well-known method in OO is the optimal computing budget allocation (OCBA). It builds the optimality conditions for the number of samples allocated to each design, and the sample allocation that satisfies the optimality conditions is shown to asymptotically maximize the probability of correct selection for the best design. In this paper, we investigate two popular OCBA algorithms. With known variances for samples of each design, we characterize their convergence rates with respect to different performance measures. We first demonstrate that the two OCBA algorithms achieve the optimal convergence rate under measures of probability of correct selection and expected opportunity cost. It fills the void of convergence analysis for OCBA algorithms. Next, we extend our analysis to the measure of cumulative regret, a main measure studied in the field of machine learning. We show that with minor modification, the two OCBA algorithms can reach the optimal convergence rate under cumulative regret. It indicates the potential of broader use of algorithms designed based on the OCBA optimality conditions.
Asymptotic Optimality of Myopic Ranking and Selection Procedures
Nov 27, 2022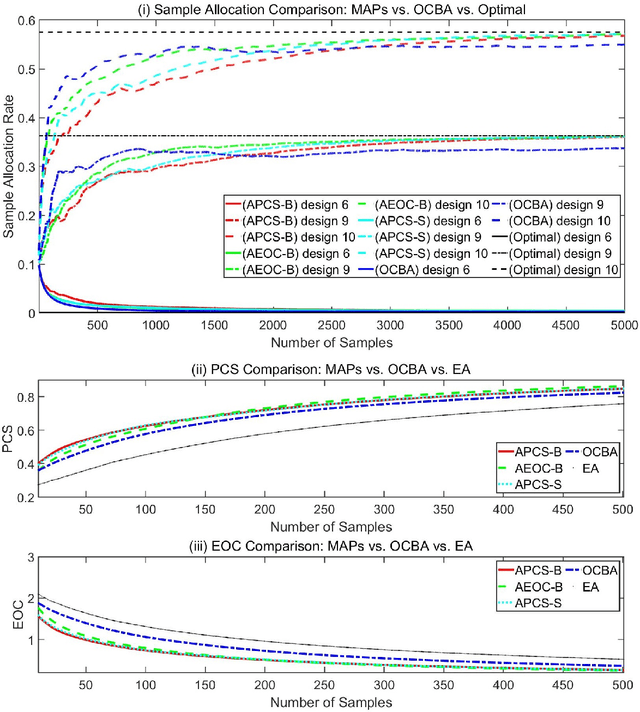
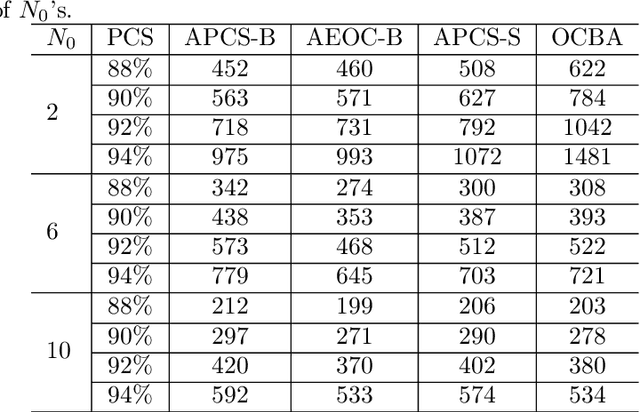
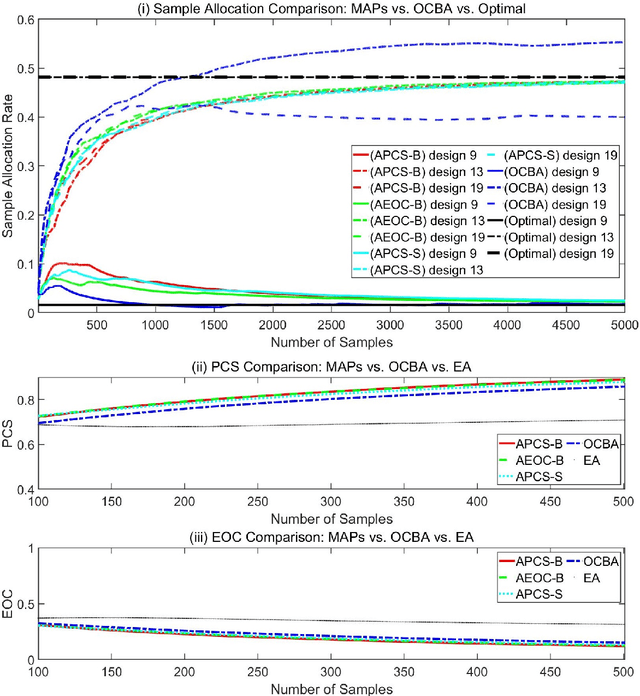
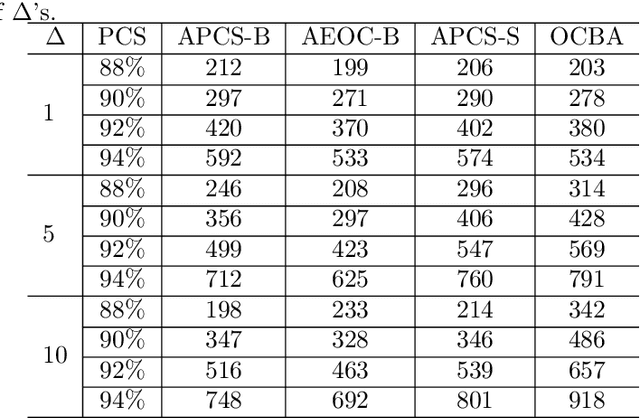
Abstract:Ranking and selection (R&S) is a popular model for studying discrete-event dynamic systems. It aims to select the best design (the design with the largest mean performance) from a finite set, where the mean of each design is unknown and has to be learned by samples. Great research efforts have been devoted to this problem in the literature for developing procedures with superior empirical performance and showing their optimality. In these efforts, myopic procedures were popular. They select the best design using a 'naive' mechanism of iteratively and myopically improving an approximation of the objective measure. Although they are based on simple heuristics and lack theoretical support, they turned out highly effective, and often achieved competitive empirical performance compared to procedures that were proposed later and shown to be asymptotically optimal. In this paper, we theoretically analyze these myopic procedures and prove that they also satisfy the optimality conditions of R&S, just like some other popular R&S methods. It explains the good performance of myopic procedures in various numerical tests, and provides good insight into the structure and theoretical development of efficient R&S procedures.
On the Finite-Time Performance of the Knowledge Gradient Algorithm
Jun 17, 2022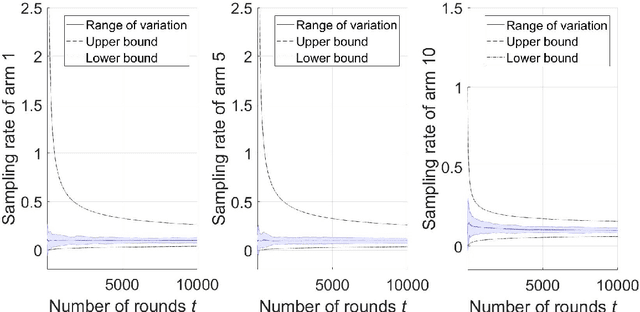
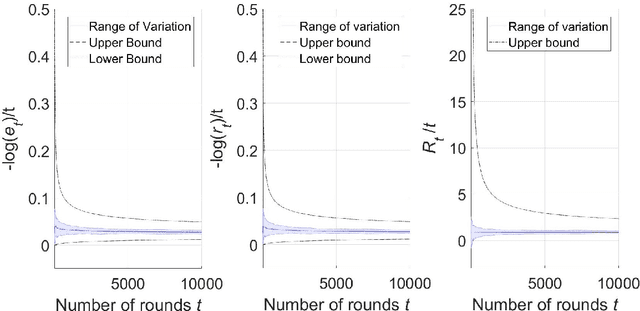
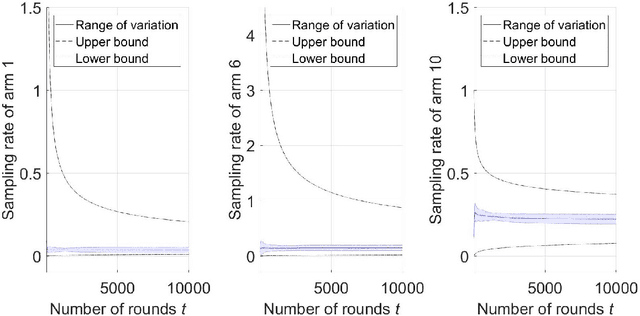
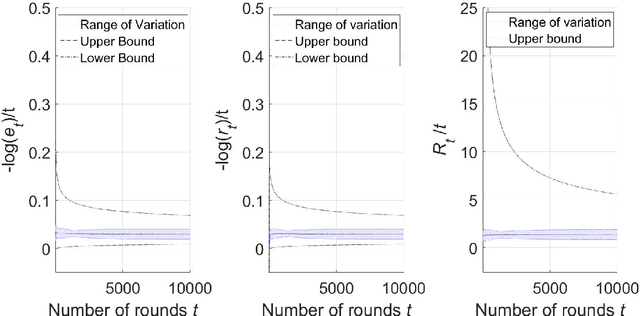
Abstract:The knowledge gradient (KG) algorithm is a popular and effective algorithm for the best arm identification (BAI) problem. Due to the complex calculation of KG, theoretical analysis of this algorithm is difficult, and existing results are mostly about the asymptotic performance of it, e.g., consistency, asymptotic sample allocation, etc. In this research, we present new theoretical results about the finite-time performance of the KG algorithm. Under independent and normally distributed rewards, we derive lower bounds and upper bounds for the probability of error and simple regret of the algorithm. With these bounds, existing asymptotic results become simple corollaries. We also show the performance of the algorithm for the multi-armed bandit (MAB) problem. These developments not only extend the existing analysis of the KG algorithm, but can also be used to analyze other improvement-based algorithms. Last, we use numerical experiments to further demonstrate the finite-time behavior of the KG algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge