Scale-aware Super-resolution Network with Dual Affinity Learning for Lesion Segmentation from Medical Images

Convolutional Neural Networks (CNNs) have shown remarkable progress in medical image segmentation. However, lesion segmentation remains a challenge to state-of-the-art CNN-based algorithms due to the variance in scales and shapes. On the one hand, tiny lesions are hard to be delineated precisely from the medical images which are often of low resolutions. On the other hand, segmenting large-size lesions requires large receptive fields, which exacerbates the first challenge. In this paper, we present a scale-aware super-resolution network to adaptively segment lesions of various sizes from the low-resolution medical images. Our proposed network contains dual branches to simultaneously conduct lesion mask super-resolution and lesion image super-resolution. The image super-resolution branch will provide more detailed features for the segmentation branch, i.e., the mask super-resolution branch, for fine-grained segmentation. Meanwhile, we introduce scale-aware dilated convolution blocks into the multi-task decoders to adaptively adjust the receptive fields of the convolutional kernels according to the lesion sizes. To guide the segmentation branch to learn from richer high-resolution features, we propose a feature affinity module and a scale affinity module to enhance the multi-task learning of the dual branches. On multiple challenging lesion segmentation datasets, our proposed network achieved consistent improvements compared to other state-of-the-art methods.

Convergence Rate Analysis for Optimal Computing Budget Allocation Algorithms

Ordinal optimization (OO) is a widely-studied technique for optimizing discrete-event dynamic systems (DEDS). It evaluates the performance of the system designs in a finite set by sampling and aims to correctly make ordinal comparison of the designs. A well-known method in OO is the optimal computing budget allocation (OCBA). It builds the optimality conditions for the number of samples allocated to each design, and the sample allocation that satisfies the optimality conditions is shown to asymptotically maximize the probability of correct selection for the best design. In this paper, we investigate two popular OCBA algorithms. With known variances for samples of each design, we characterize their convergence rates with respect to different performance measures. We first demonstrate that the two OCBA algorithms achieve the optimal convergence rate under measures of probability of correct selection and expected opportunity cost. It fills the void of convergence analysis for OCBA algorithms. Next, we extend our analysis to the measure of cumulative regret, a main measure studied in the field of machine learning. We show that with minor modification, the two OCBA algorithms can reach the optimal convergence rate under cumulative regret. It indicates the potential of broader use of algorithms designed based on the OCBA optimality conditions.

Asymptotic Optimality of Myopic Ranking and Selection Procedures

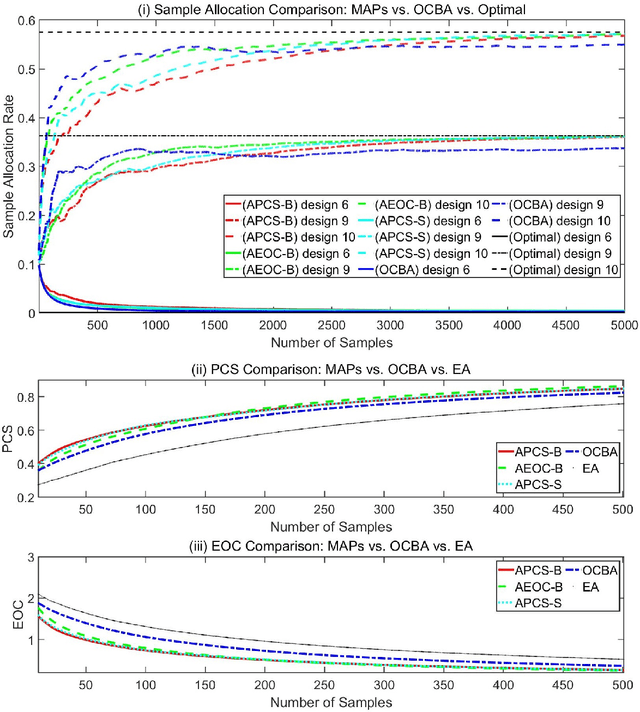
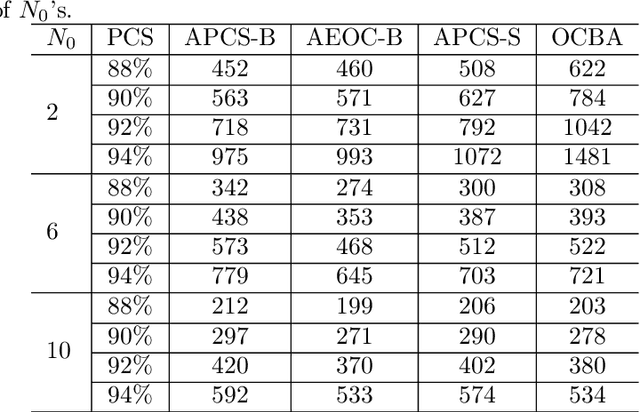
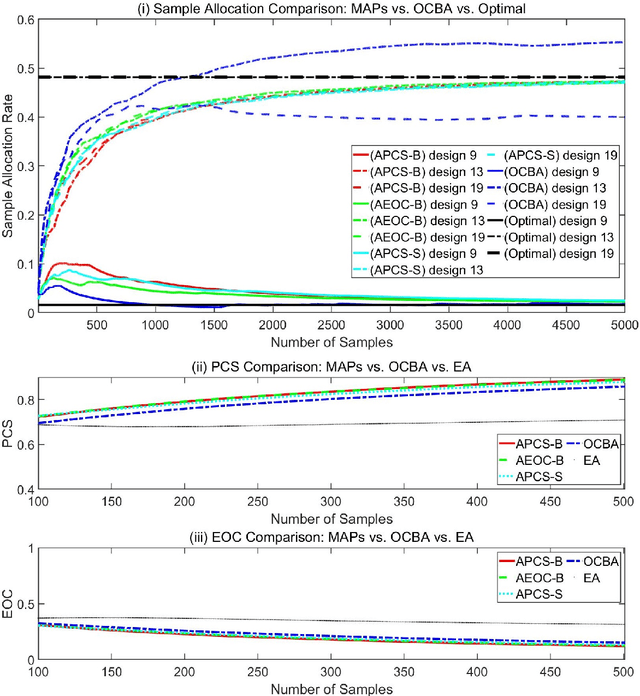
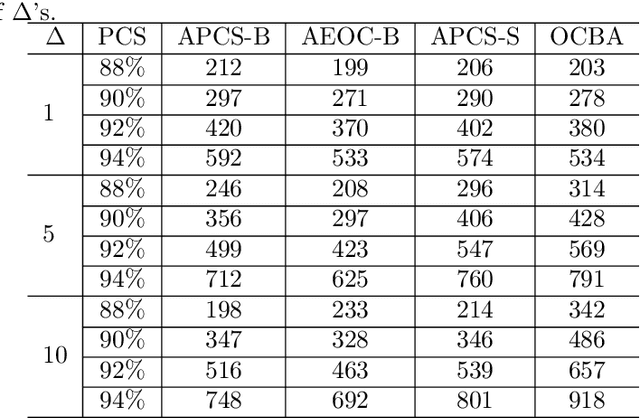
Ranking and selection (R&S) is a popular model for studying discrete-event dynamic systems. It aims to select the best design (the design with the largest mean performance) from a finite set, where the mean of each design is unknown and has to be learned by samples. Great research efforts have been devoted to this problem in the literature for developing procedures with superior empirical performance and showing their optimality. In these efforts, myopic procedures were popular. They select the best design using a 'naive' mechanism of iteratively and myopically improving an approximation of the objective measure. Although they are based on simple heuristics and lack theoretical support, they turned out highly effective, and often achieved competitive empirical performance compared to procedures that were proposed later and shown to be asymptotically optimal. In this paper, we theoretically analyze these myopic procedures and prove that they also satisfy the optimality conditions of R&S, just like some other popular R&S methods. It explains the good performance of myopic procedures in various numerical tests, and provides good insight into the structure and theoretical development of efficient R&S procedures.

On the Finite-Time Performance of the Knowledge Gradient Algorithm

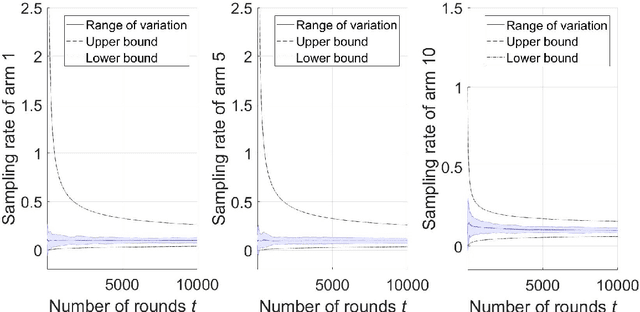
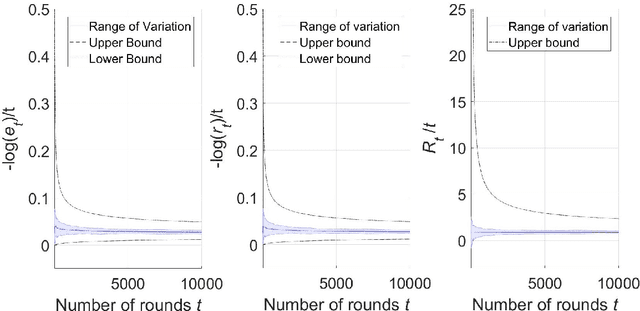
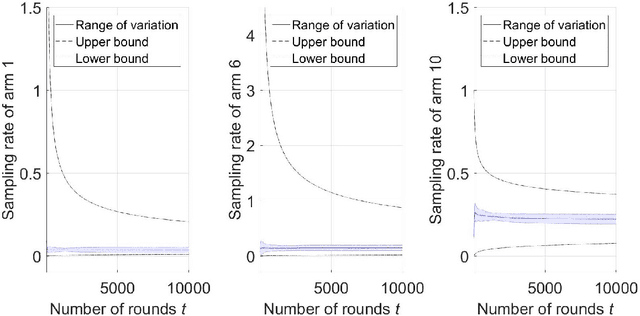
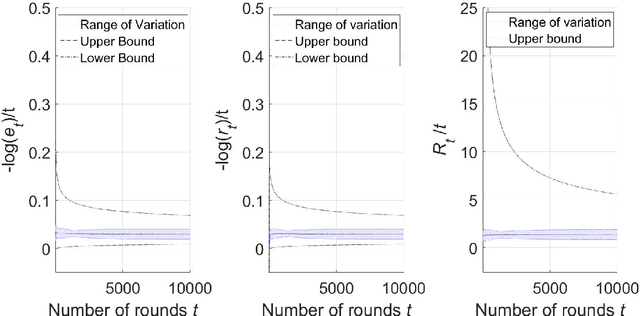
The knowledge gradient (KG) algorithm is a popular and effective algorithm for the best arm identification (BAI) problem. Due to the complex calculation of KG, theoretical analysis of this algorithm is difficult, and existing results are mostly about the asymptotic performance of it, e.g., consistency, asymptotic sample allocation, etc. In this research, we present new theoretical results about the finite-time performance of the KG algorithm. Under independent and normally distributed rewards, we derive lower bounds and upper bounds for the probability of error and simple regret of the algorithm. With these bounds, existing asymptotic results become simple corollaries. We also show the performance of the algorithm for the multi-armed bandit (MAB) problem. These developments not only extend the existing analysis of the KG algorithm, but can also be used to analyze other improvement-based algorithms. Last, we use numerical experiments to further demonstrate the finite-time behavior of the KG algorithm.

Dual-Consistency Semi-Supervised Learning with Uncertainty Quantification for COVID-19 Lesion Segmentation from CT Images

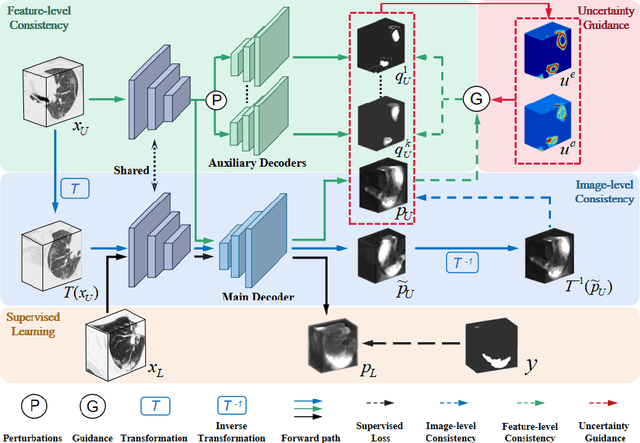
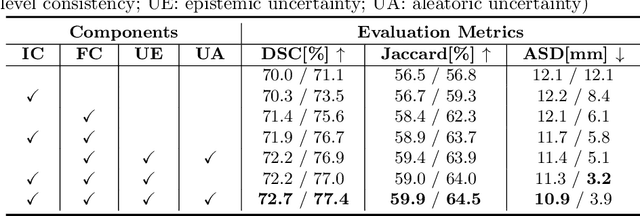
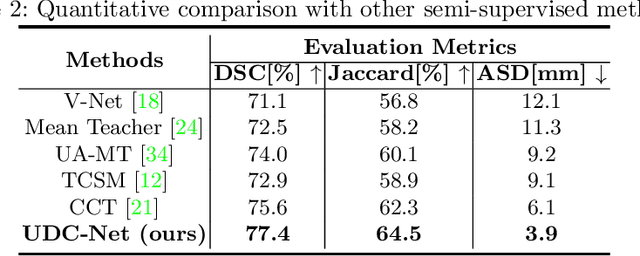
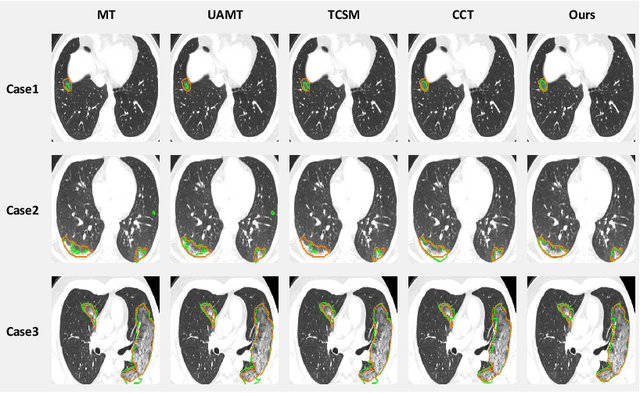
The novel coronavirus disease 2019 (COVID-19) characterized by atypical pneumonia has caused millions of deaths worldwide. Automatically segmenting lesions from chest Computed Tomography (CT) is a promising way to assist doctors in COVID-19 screening, treatment planning, and follow-up monitoring. However, voxel-wise annotations are extremely expert-demanding and scarce, especially when it comes to novel diseases, while an abundance of unlabeled data could be available. To tackle the challenge of limited annotations, in this paper, we propose an uncertainty-guided dual-consistency learning network (UDC-Net) for semi-supervised COVID-19 lesion segmentation from CT images. Specifically, we present a dual-consistency learning scheme that simultaneously imposes image transformation equivalence and feature perturbation invariance to effectively harness the knowledge from unlabeled data. We then quantify both the epistemic uncertainty and the aleatoric uncertainty and employ them together to guide the consistency regularization for more reliable unsupervised learning. Extensive experiments showed that our proposed UDC-Net improves the fully supervised method by 6.3% in Dice and outperforms other competitive semi-supervised approaches by significant margins, demonstrating high potential in real-world clinical practice.