Geometry Contrastive Learning on Heterogeneous Graphs

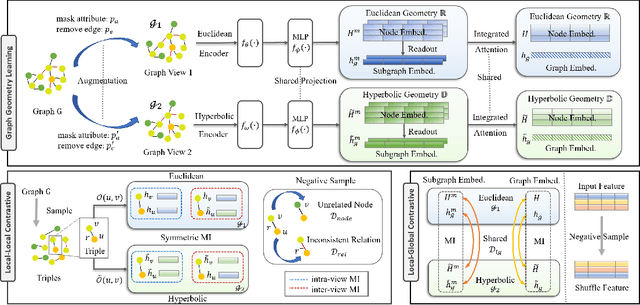
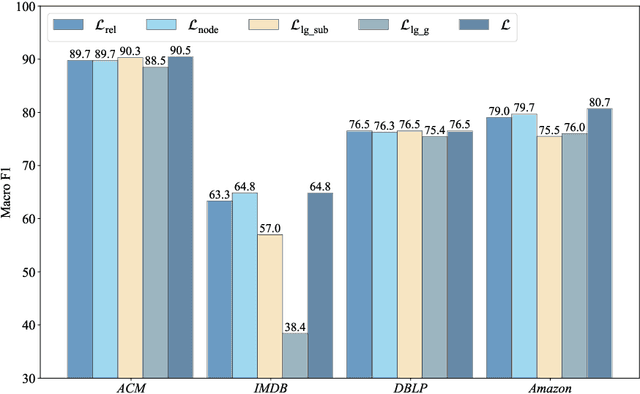
Self-supervised learning (especially contrastive learning) methods on heterogeneous graphs can effectively get rid of the dependence on supervisory data. Meanwhile, most existing representation learning methods embed the heterogeneous graphs into a single geometric space, either Euclidean or hyperbolic. This kind of single geometric view is usually not enough to observe the complete picture of heterogeneous graphs due to their rich semantics and complex structures. Under these observations, this paper proposes a novel self-supervised learning method, termed as Geometry Contrastive Learning (GCL), to better represent the heterogeneous graphs when supervisory data is unavailable. GCL views a heterogeneous graph from Euclidean and hyperbolic perspective simultaneously, aiming to make a strong merger of the ability of modeling rich semantics and complex structures, which is expected to bring in more benefits for downstream tasks. GCL maximizes the mutual information between two geometric views by contrasting representations at both local-local and local-global semantic levels. Extensive experiments on four benchmarks data sets show that the proposed approach outperforms the strong baselines, including both unsupervised methods and supervised methods, on three tasks, including node classification, node clustering and similarity search.

Ultrahyperbolic Knowledge Graph Embeddings

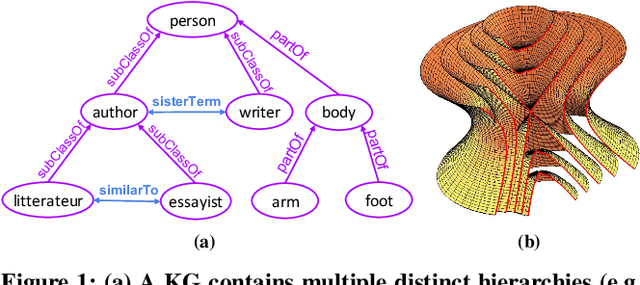
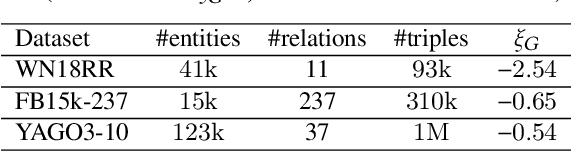
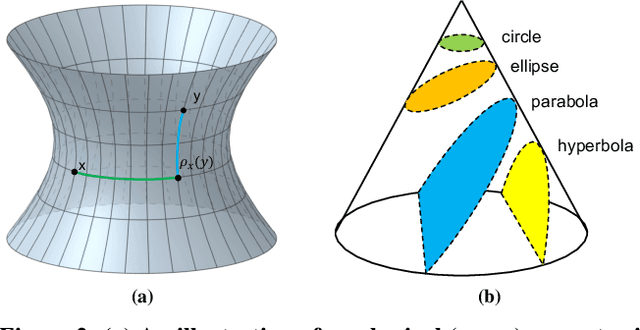
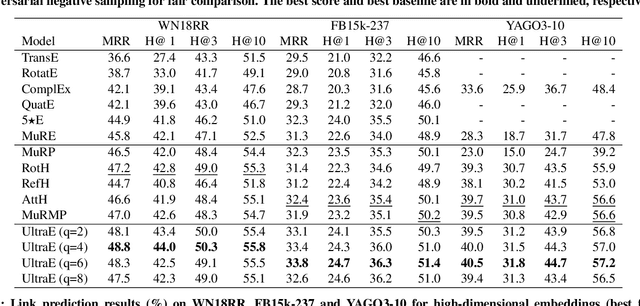
Recent knowledge graph (KG) embeddings have been advanced by hyperbolic geometry due to its superior capability for representing hierarchies. The topological structures of real-world KGs, however, are rather heterogeneous, i.e., a KG is composed of multiple distinct hierarchies and non-hierarchical graph structures. Therefore, a homogeneous (either Euclidean or hyperbolic) geometry is not sufficient for fairly representing such heterogeneous structures. To capture the topological heterogeneity of KGs, we present an ultrahyperbolic KG embedding (UltraE) in an ultrahyperbolic (or pseudo-Riemannian) manifold that seamlessly interleaves hyperbolic and spherical manifolds. In particular, we model each relation as a pseudo-orthogonal transformation that preserves the pseudo-Riemannian bilinear form. The pseudo-orthogonal transformation is decomposed into various operators (i.e., circular rotations, reflections and hyperbolic rotations), allowing for simultaneously modeling heterogeneous structures as well as complex relational patterns. Experimental results on three standard KGs show that UltraE outperforms previous Euclidean- and hyperbolic-based approaches.

Multi-View Substructure Learning for Drug-Drug Interaction Prediction

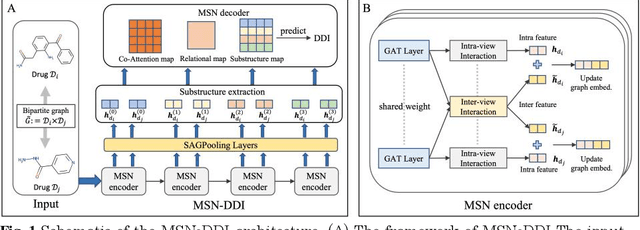
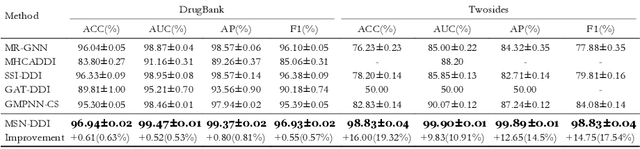
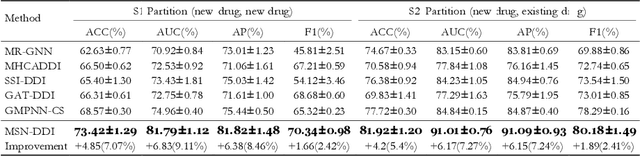
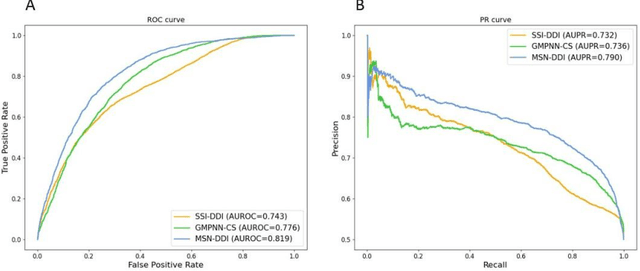
Drug-drug interaction (DDI) prediction provides a drug combination strategy for systemically effective treatment. Previous studies usually model drug information constrained on a single view such as the drug itself, leading to incomplete and noisy information, which limits the accuracy of DDI prediction. In this work, we propose a novel multi- view drug substructure network for DDI prediction (MSN-DDI), which learns chemical substructures from both the representations of the single drug (intra-view) and the drug pair (inter-view) simultaneously and utilizes the substructures to update the drug representation iteratively. Comprehensive evaluations demonstrate that MSN-DDI has almost solved DDI prediction for existing drugs by achieving a relatively improved accuracy of 19.32% and an over 99% accuracy under the transductive setting. More importantly, MSN-DDI exhibits better generalization ability to unseen drugs with a relatively improved accuracy of 7.07% under more challenging inductive scenarios. Finally, MSN-DDI improves prediction performance for real-world DDI applications to new drugs.

Multi-Graph Fusion Networks for Urban Region Embedding

Learning the embeddings for urban regions from human mobility data can reveal the functionality of regions, and then enables the correlated but distinct tasks such as crime prediction. Human mobility data contains rich but abundant information, which yields to the comprehensive region embeddings for cross domain tasks. In this paper, we propose multi-graph fusion networks (MGFN) to enable the cross domain prediction tasks. First, we integrate the graphs with spatio-temporal similarity as mobility patterns through a mobility graph fusion module. Then, in the mobility pattern joint learning module, we design the multi-level cross-attention mechanism to learn the comprehensive embeddings from multiple mobility patterns based on intra-pattern and inter-pattern messages. Finally, we conduct extensive experiments on real-world urban datasets. Experimental results demonstrate that the proposed MGFN outperforms the state-of-the-art methods by up to 12.35% improvement.

Semi-Riemannian Graph Convolutional Networks

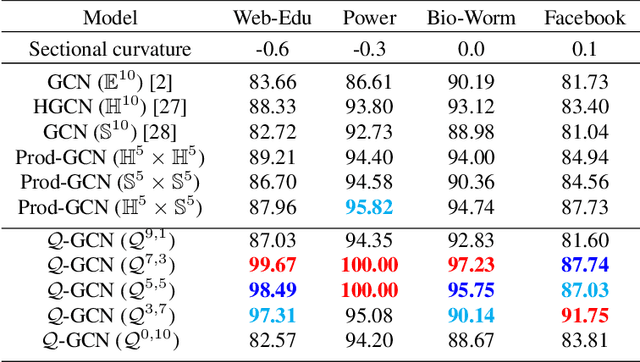
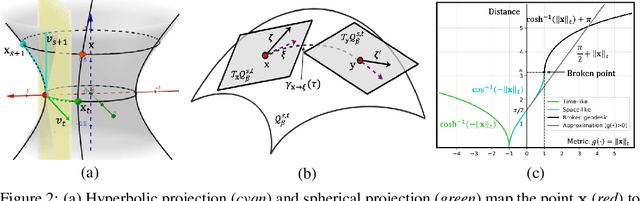
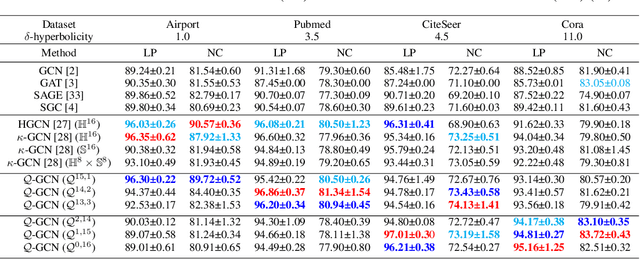
Graph Convolutional Networks (GCNs) are typically studied through the lens of Euclidean geometry. Non-Euclidean Riemannian manifolds provide specific inductive biases for embedding hierarchical or spherical data, but cannot align well with data of mixed topologies. We consider a larger class of semi-Riemannian manifolds with indefinite metric that generalize hyperboloid and sphere as well as their submanifolds. We develop new geodesic tools that allow for extending neural network operations into geodesically disconnected semi-Riemannian manifolds. As a consequence, we derive a principled Semi-Riemannian GCN that first models data in semi-Riemannian manifolds of constant nonzero curvature in the context of graph neural networks. Our method provides a geometric inductive bias that is sufficiently flexible to model mixed heterogeneous topologies like hierarchical graphs with cycles. Empirical results demonstrate that our method outperforms Riemannian counterparts when embedding graphs of complex topologies.

Graph Geometry Interaction Learning

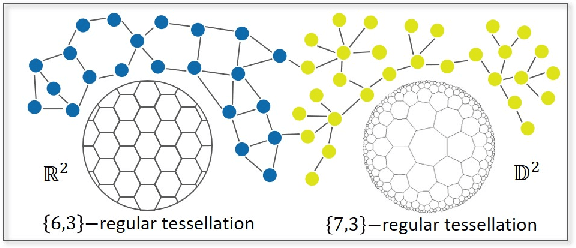
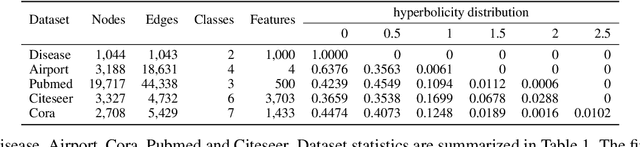
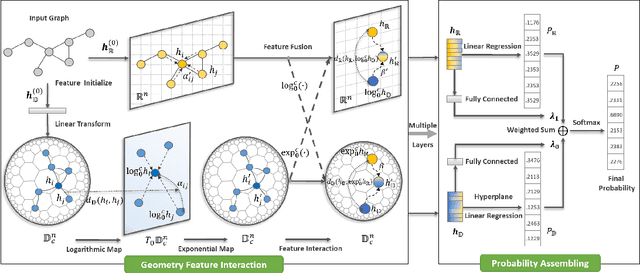
While numerous approaches have been developed to embed graphs into either Euclidean or hyperbolic spaces, they do not fully utilize the information available in graphs, or lack the flexibility to model intrinsic complex graph geometry. To utilize the strength of both Euclidean and hyperbolic geometries, we develop a novel Geometry Interaction Learning (GIL) method for graphs, a well-suited and efficient alternative for learning abundant geometric properties in graph. GIL captures a more informative internal structural features with low dimensions while maintaining conformal invariance of each space. Furthermore, our method endows each node the freedom to determine the importance of each geometry space via a flexible dual feature interaction learning and probability assembling mechanism. Promising experimental results are presented for five benchmark datasets on node classification and link prediction tasks.