Ultrahyperbolic Knowledge Graph Embeddings
Paper and Code
Jun 01, 2022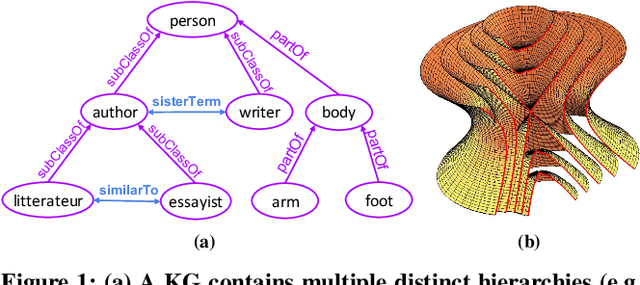
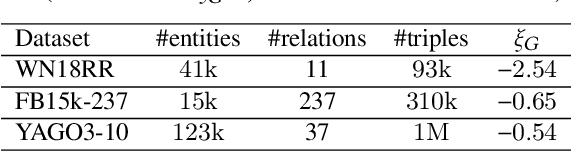
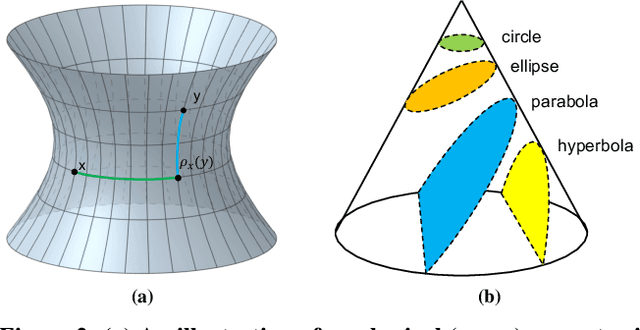
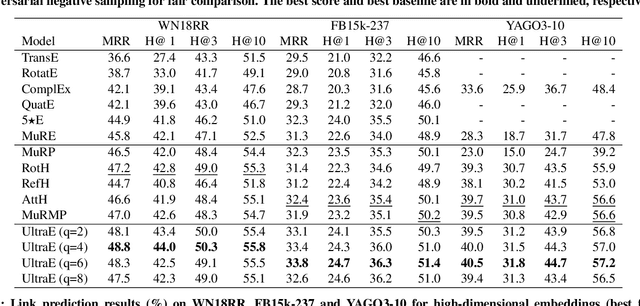
Recent knowledge graph (KG) embeddings have been advanced by hyperbolic geometry due to its superior capability for representing hierarchies. The topological structures of real-world KGs, however, are rather heterogeneous, i.e., a KG is composed of multiple distinct hierarchies and non-hierarchical graph structures. Therefore, a homogeneous (either Euclidean or hyperbolic) geometry is not sufficient for fairly representing such heterogeneous structures. To capture the topological heterogeneity of KGs, we present an ultrahyperbolic KG embedding (UltraE) in an ultrahyperbolic (or pseudo-Riemannian) manifold that seamlessly interleaves hyperbolic and spherical manifolds. In particular, we model each relation as a pseudo-orthogonal transformation that preserves the pseudo-Riemannian bilinear form. The pseudo-orthogonal transformation is decomposed into various operators (i.e., circular rotations, reflections and hyperbolic rotations), allowing for simultaneously modeling heterogeneous structures as well as complex relational patterns. Experimental results on three standard KGs show that UltraE outperforms previous Euclidean- and hyperbolic-based approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge