The Entrapment Problem in Random Walk Decentralized Learning

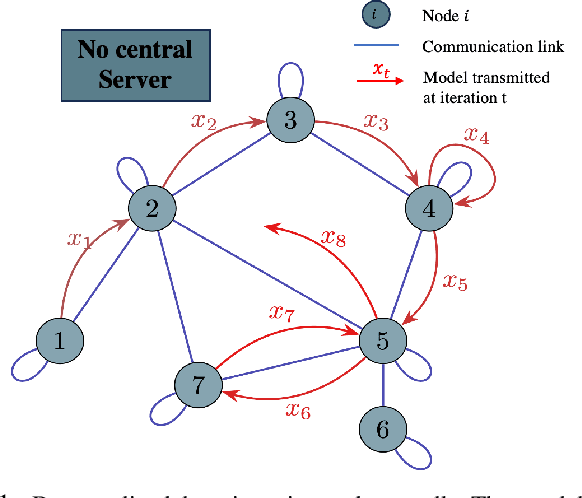
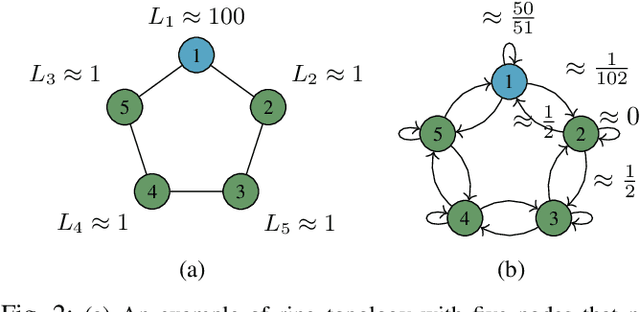
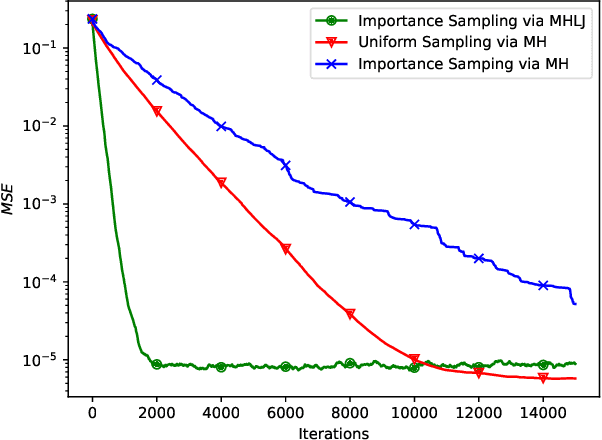
This paper explores decentralized learning in a graph-based setting, where data is distributed across nodes. We investigate a decentralized SGD algorithm that utilizes a random walk to update a global model based on local data. Our focus is on designing the transition probability matrix to speed up convergence. While importance sampling can enhance centralized learning, its decentralized counterpart, using the Metropolis-Hastings (MH) algorithm, can lead to the entrapment problem, where the random walk becomes stuck at certain nodes, slowing convergence. To address this, we propose the Metropolis-Hastings with L\'evy Jumps (MHLJ) algorithm, which incorporates random perturbations (jumps) to overcome entrapment. We theoretically establish the convergence rate and error gap of MHLJ and validate our findings through numerical experiments.

Self-Duplicating Random Walks for Resilient Decentralized Learning on Graphs

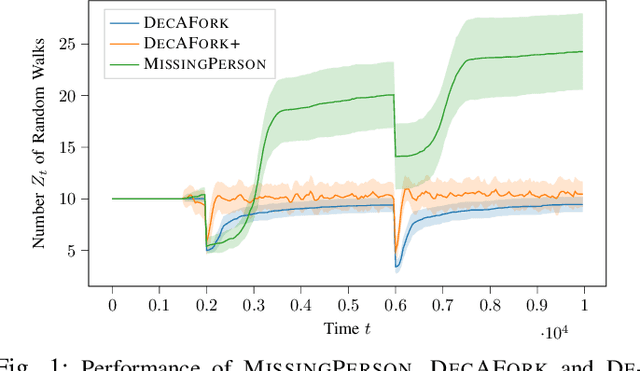
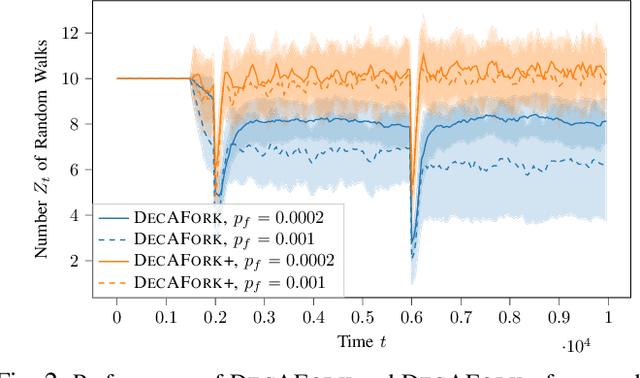
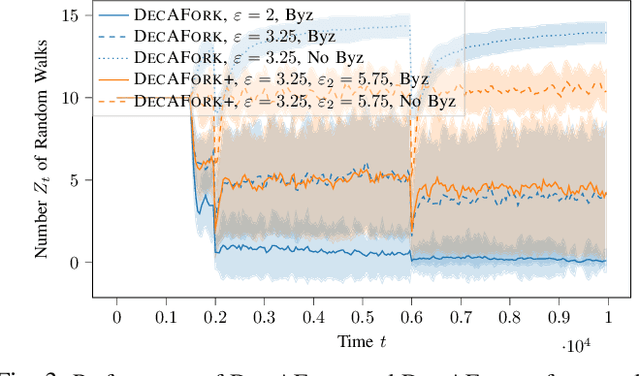
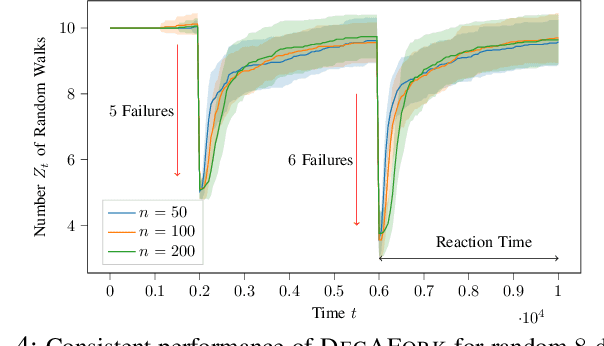
Consider the setting of multiple random walks (RWs) on a graph executing a certain computational task. For instance, in decentralized learning via RWs, a model is updated at each iteration based on the local data of the visited node and then passed to a randomly chosen neighbor. RWs can fail due to node or link failures. The goal is to maintain a desired number of RWs to ensure failure resilience. Achieving this is challenging due to the lack of a central entity to track which RWs have failed to replace them with new ones by forking (duplicating) surviving ones. Without duplications, the number of RWs will eventually go to zero, causing a catastrophic failure of the system. We propose a decentralized algorithm called DECAFORK that can maintain the number of RWs in the graph around a desired value even in the presence of arbitrary RW failures. Nodes continuously estimate the number of surviving RWs by estimating their return time distribution and fork the RWs when failures are likely to happen. We present extensive numerical simulations that show the performance of DECAFORK regarding fast detection and reaction to failures. We further present theoretical guarantees on the performance of this algorithm.

Adaptive Stochastic Gradient Descent for Fast and Communication-Efficient Distributed Learning

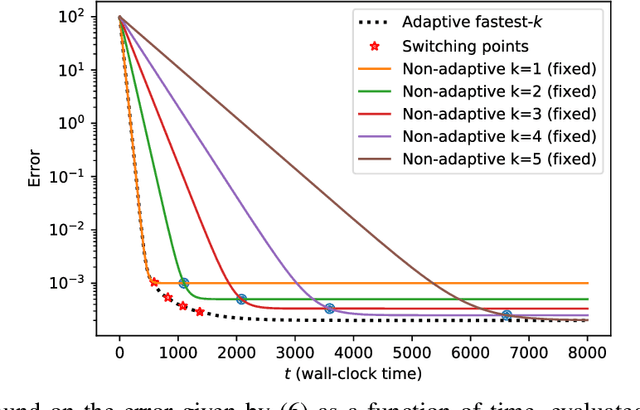
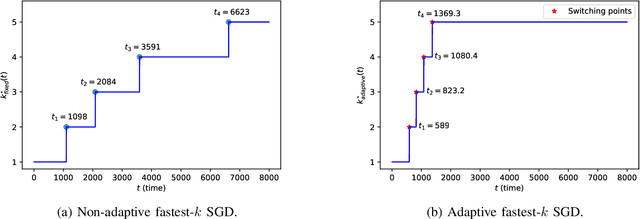
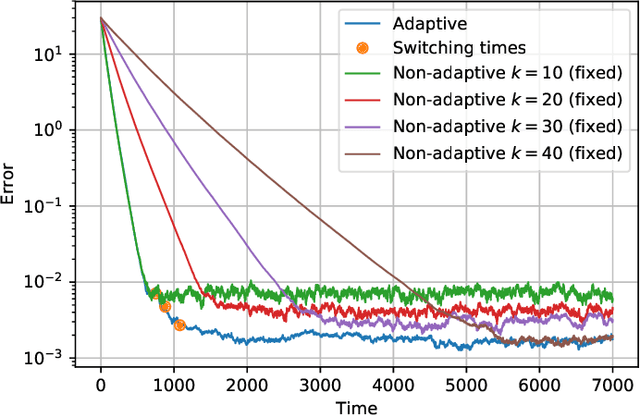
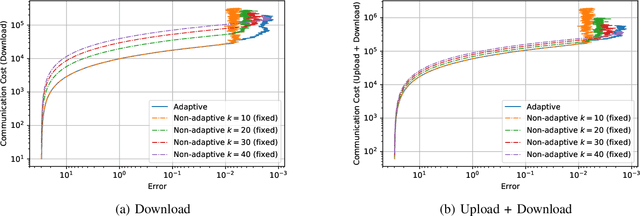
We consider the setting where a master wants to run a distributed stochastic gradient descent (SGD) algorithm on $n$ workers, each having a subset of the data. Distributed SGD may suffer from the effect of stragglers, i.e., slow or unresponsive workers who cause delays. One solution studied in the literature is to wait at each iteration for the responses of the fastest $k<n$ workers before updating the model, where $k$ is a fixed parameter. The choice of the value of $k$ presents a trade-off between the runtime (i.e., convergence rate) of SGD and the error of the model. Towards optimizing the error-runtime trade-off, we investigate distributed SGD with adaptive~$k$, i.e., varying $k$ throughout the runtime of the algorithm. We first design an adaptive policy for varying $k$ that optimizes this trade-off based on an upper bound on the error as a function of the wall-clock time that we derive. Then, we propose and implement an algorithm for adaptive distributed SGD that is based on a statistical heuristic. Our results show that the adaptive version of distributed SGD can reach lower error values in less time compared to non-adaptive implementations. Moreover, the results also show that the adaptive version is communication-efficient, where the amount of communication required between the master and the workers is less than that of non-adaptive versions.

Walk for Learning: A Random Walk Approach for Federated Learning from Heterogeneous Data

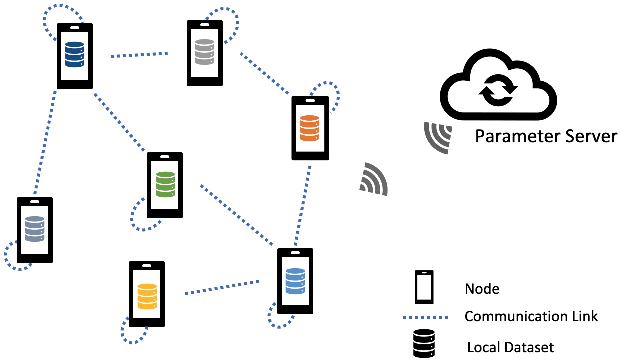
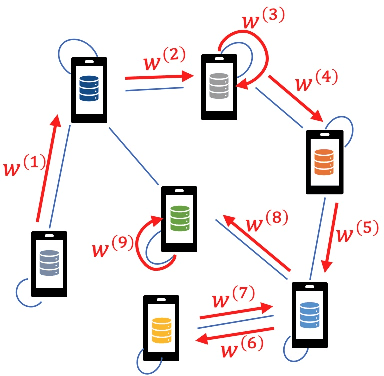
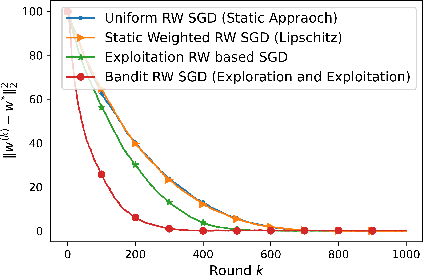
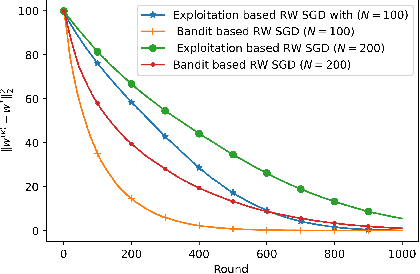
We consider the problem of a Parameter Server (PS) that wishes to learn a model that fits data distributed on the nodes of a graph. We focus on Federated Learning (FL) as a canonical application. One of the main challenges of FL is the communication bottleneck between the nodes and the parameter server. A popular solution in the literature is to allow each node to do several local updates on the model in each iteration before sending it back to the PS. While this mitigates the communication bottleneck, the statistical heterogeneity of the data owned by the different nodes has proven to delay convergence and bias the model. In this work, we study random walk (RW) learning algorithms for tackling the communication and data heterogeneity problems. The main idea is to leverage available direct connections among the nodes themselves, which are typically "cheaper" than the communication to the PS. In a random walk, the model is thought of as a "baton" that is passed from a node to one of its neighbors after being updated in each iteration. The challenge in designing the RW is the data heterogeneity and the uncertainty about the data distributions. Ideally, we would want to visit more often nodes that hold more informative data. We cast this problem as a sleeping multi-armed bandit (MAB) to design a near-optimal node sampling strategy that achieves variance-reduced gradient estimates and approaches sub-linearly the optimal sampling strategy. Based on this framework, we present an adaptive random walk learning algorithm. We provide theoretical guarantees on its convergence. Our numerical results validate our theoretical findings and show that our algorithm outperforms existing random walk algorithms.

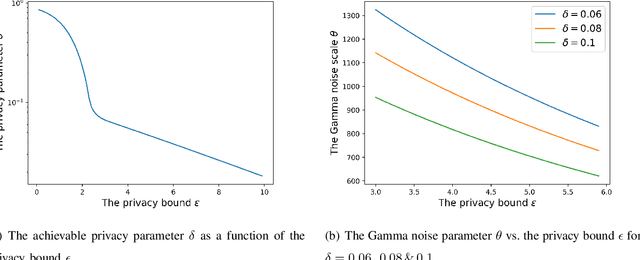
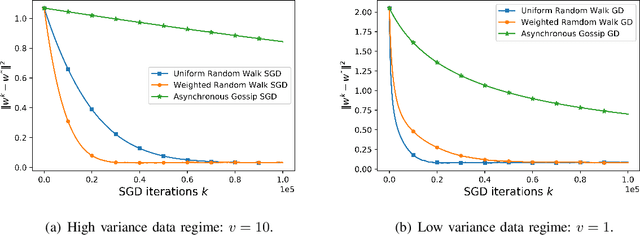
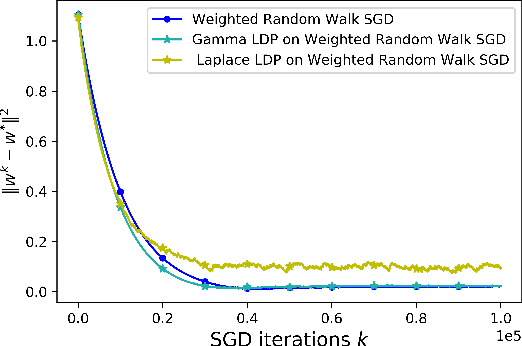
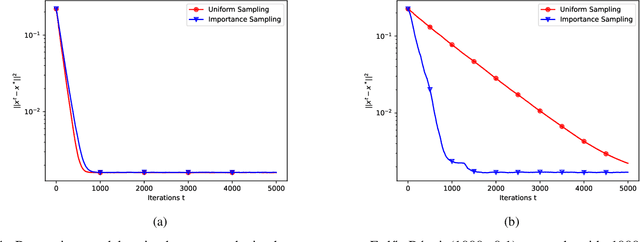
Private Weighted Random Walk Stochastic Gradient Descent

We consider a decentralized learning setting in which data is distributed over nodes in a graph. The goal is to learn a global model on the distributed data without involving any central entity that needs to be trusted. While gossip-based stochastic gradient descent (SGD) can be used to achieve this learning objective, it incurs high communication and computation costs, since it has to wait for all the local models at all the nodes to converge. To speed up the convergence, we propose instead to study random walk based SGD in which a global model is updated based on a random walk on the graph. We propose two algorithms based on two types of random walks that achieve, in a decentralized way, uniform sampling and importance sampling of the data. We provide a non-asymptotic analysis on the rate of convergence, taking into account the constants related to the data and the graph. Our numerical results show that the weighted random walk based algorithm has a better performance for high-variance data. Moreover, we propose a privacy-preserving random walk algorithm that achieves local differential privacy based on a Gamma noise mechanism that we propose. We also give numerical results on the convergence of this algorithm and show that it outperforms additive Laplace-based privacy mechanisms.

Mechanisms for Hiding Sensitive Genotypes with Information-Theoretic Privacy

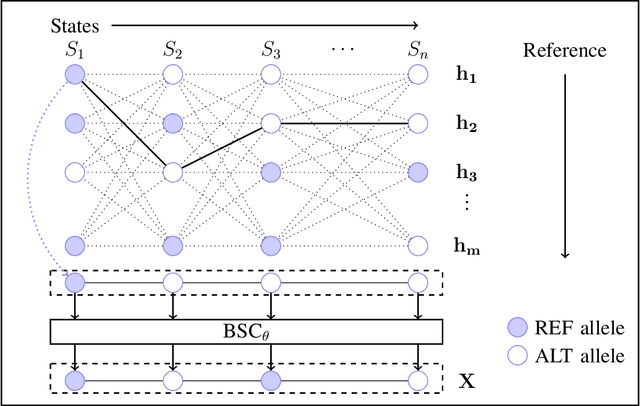
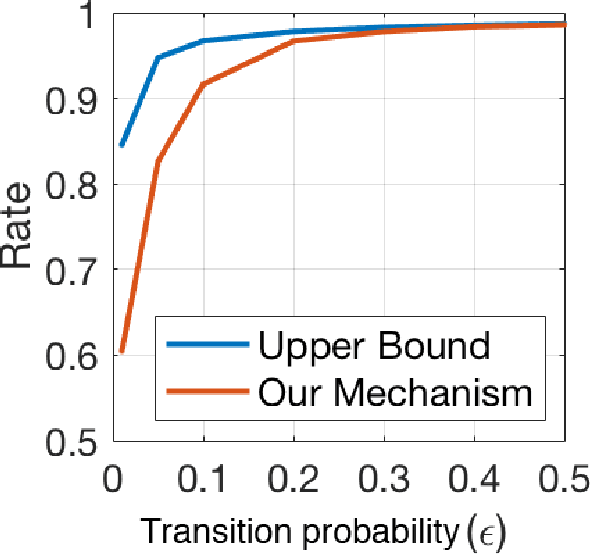
The growing availability of personal genomics services comes with increasing concerns for genomic privacy. Individuals may wish to withhold sensitive genotypes that contain critical health-related information when sharing their data with such services. A straightforward solution that masks only the sensitive genotypes does not ensure privacy due to the correlation structure within the genome. Here, we develop an information-theoretic mechanism for masking sensitive genotypes, which ensures no information about the sensitive genotypes is leaked. We also propose an efficient algorithmic implementation of our mechanism for genomic data governed by hidden Markov models. Our work is a step towards more rigorous control of privacy in genomic data sharing.

Adaptive Distributed Stochastic Gradient Descent for Minimizing Delay in the Presence of Stragglers

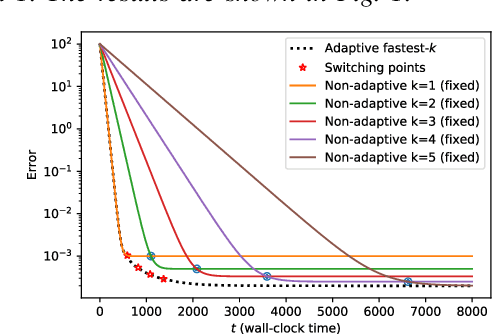
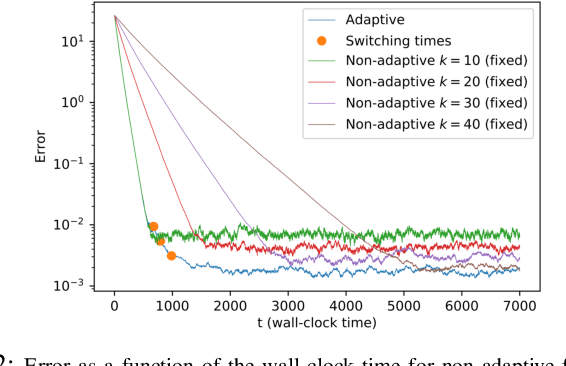
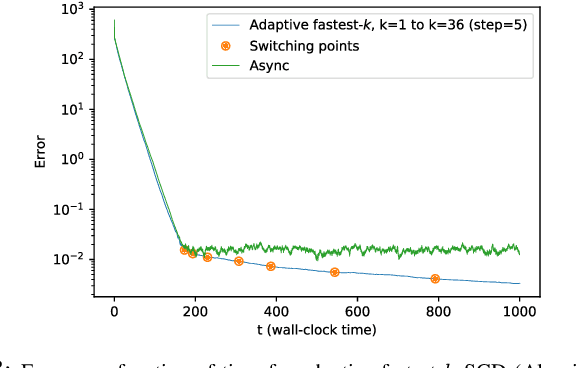
We consider the setting where a master wants to run a distributed stochastic gradient descent (SGD) algorithm on $n$ workers each having a subset of the data. Distributed SGD may suffer from the effect of stragglers, i.e., slow or unresponsive workers who cause delays. One solution studied in the literature is to wait at each iteration for the responses of the fastest $k<n$ workers before updating the model, where $k$ is a fixed parameter. The choice of the value of $k$ presents a trade-off between the runtime (i.e., convergence rate) of SGD and the error of the model. Towards optimizing the error-runtime trade-off, we investigate distributed SGD with adaptive $k$. We first design an adaptive policy for varying $k$ that optimizes this trade-off based on an upper bound on the error as a function of the wall-clock time which we derive. Then, we propose an algorithm for adaptive distributed SGD that is based on a statistical heuristic. We implement our algorithm and provide numerical simulations which confirm our intuition and theoretical analysis.

Advances and Open Problems in Federated Learning

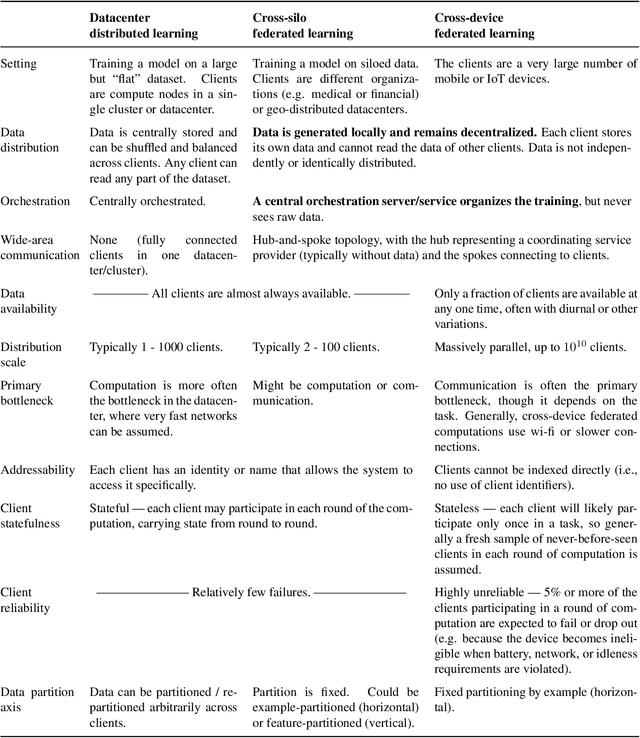
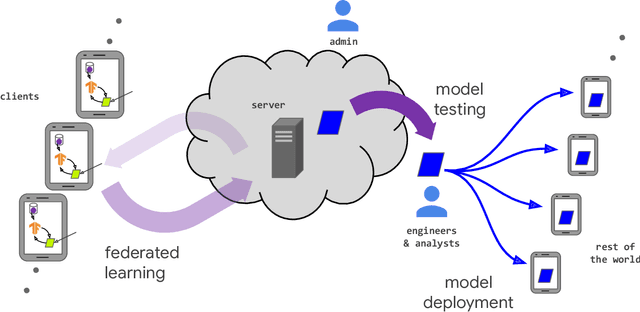
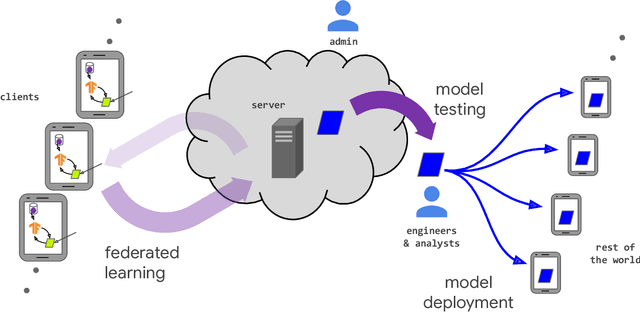
Federated learning (FL) is a machine learning setting where many clients (e.g. mobile devices or whole organizations) collaboratively train a model under the orchestration of a central server (e.g. service provider), while keeping the training data decentralized. FL embodies the principles of focused data collection and minimization, and can mitigate many of the systemic privacy risks and costs resulting from traditional, centralized machine learning and data science approaches. Motivated by the explosive growth in FL research, this paper discusses recent advances and presents an extensive collection of open problems and challenges.