Venkat Dassari
Walk for Learning: A Random Walk Approach for Federated Learning from Heterogeneous Data
Jun 01, 2022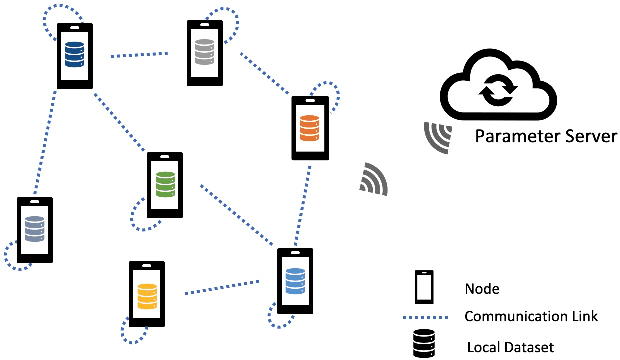
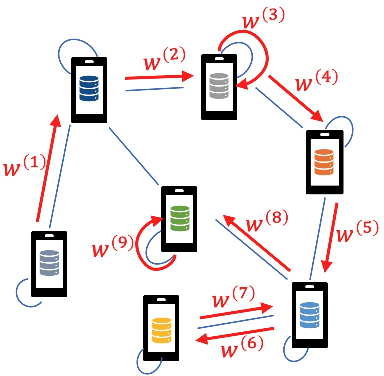
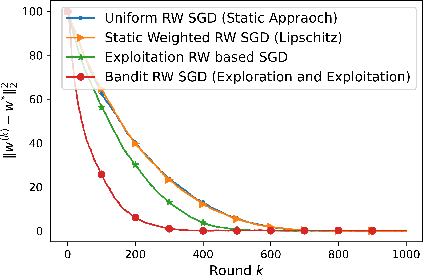
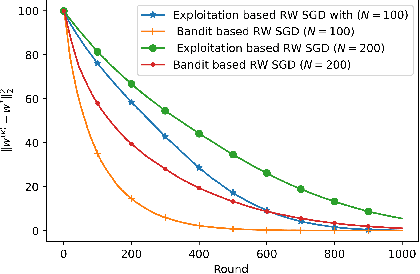
Abstract:We consider the problem of a Parameter Server (PS) that wishes to learn a model that fits data distributed on the nodes of a graph. We focus on Federated Learning (FL) as a canonical application. One of the main challenges of FL is the communication bottleneck between the nodes and the parameter server. A popular solution in the literature is to allow each node to do several local updates on the model in each iteration before sending it back to the PS. While this mitigates the communication bottleneck, the statistical heterogeneity of the data owned by the different nodes has proven to delay convergence and bias the model. In this work, we study random walk (RW) learning algorithms for tackling the communication and data heterogeneity problems. The main idea is to leverage available direct connections among the nodes themselves, which are typically "cheaper" than the communication to the PS. In a random walk, the model is thought of as a "baton" that is passed from a node to one of its neighbors after being updated in each iteration. The challenge in designing the RW is the data heterogeneity and the uncertainty about the data distributions. Ideally, we would want to visit more often nodes that hold more informative data. We cast this problem as a sleeping multi-armed bandit (MAB) to design a near-optimal node sampling strategy that achieves variance-reduced gradient estimates and approaches sub-linearly the optimal sampling strategy. Based on this framework, we present an adaptive random walk learning algorithm. We provide theoretical guarantees on its convergence. Our numerical results validate our theoretical findings and show that our algorithm outperforms existing random walk algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge