Self-Duplicating Random Walks for Resilient Decentralized Learning on Graphs

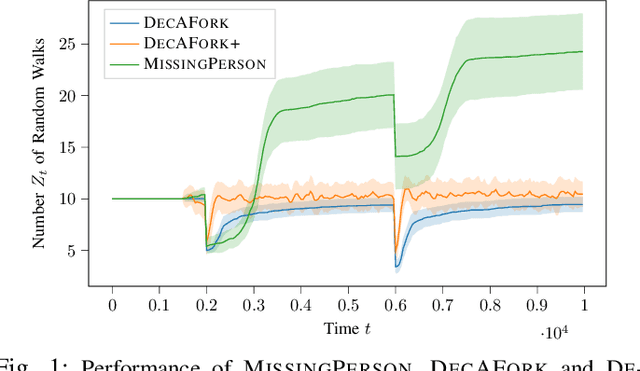
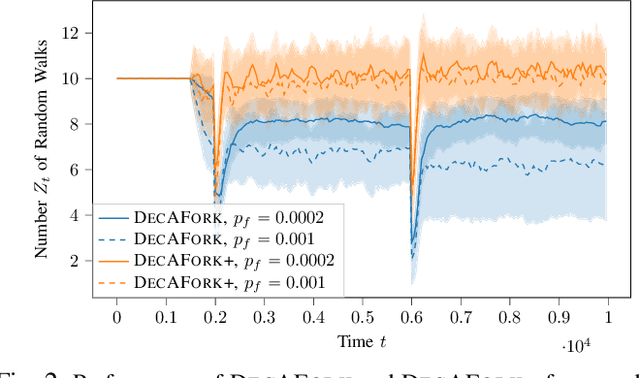
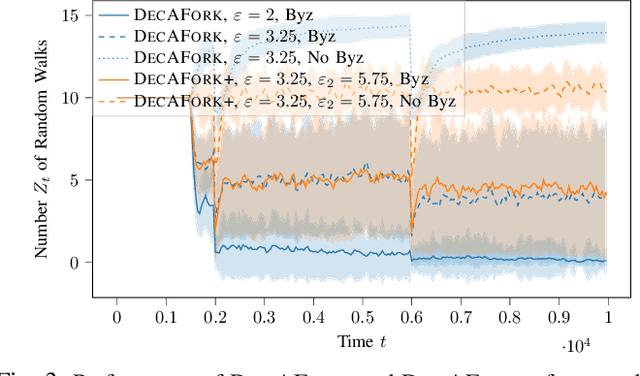
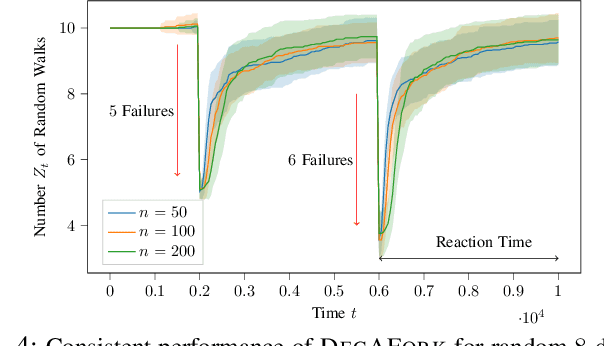
Consider the setting of multiple random walks (RWs) on a graph executing a certain computational task. For instance, in decentralized learning via RWs, a model is updated at each iteration based on the local data of the visited node and then passed to a randomly chosen neighbor. RWs can fail due to node or link failures. The goal is to maintain a desired number of RWs to ensure failure resilience. Achieving this is challenging due to the lack of a central entity to track which RWs have failed to replace them with new ones by forking (duplicating) surviving ones. Without duplications, the number of RWs will eventually go to zero, causing a catastrophic failure of the system. We propose a decentralized algorithm called DECAFORK that can maintain the number of RWs in the graph around a desired value even in the presence of arbitrary RW failures. Nodes continuously estimate the number of surviving RWs by estimating their return time distribution and fork the RWs when failures are likely to happen. We present extensive numerical simulations that show the performance of DECAFORK regarding fast detection and reaction to failures. We further present theoretical guarantees on the performance of this algorithm.

Walk for Learning: A Random Walk Approach for Federated Learning from Heterogeneous Data

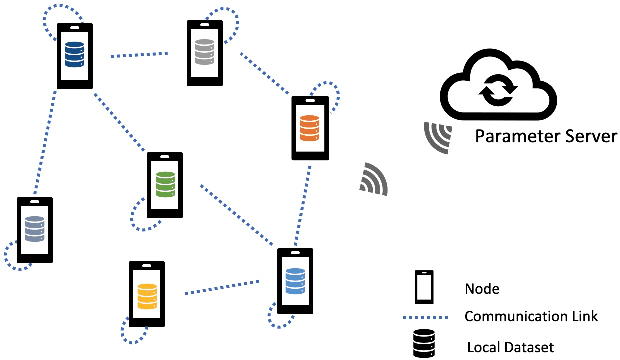
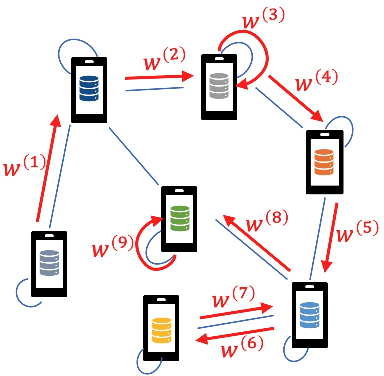
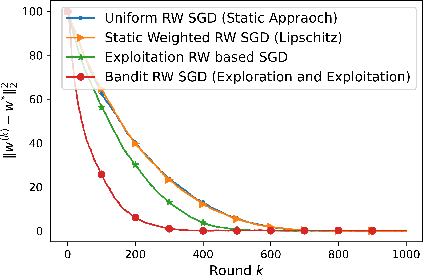
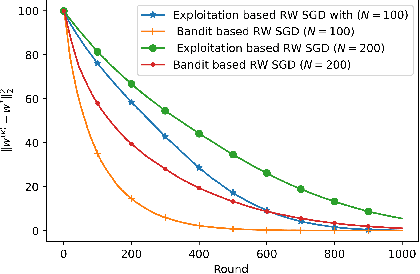
We consider the problem of a Parameter Server (PS) that wishes to learn a model that fits data distributed on the nodes of a graph. We focus on Federated Learning (FL) as a canonical application. One of the main challenges of FL is the communication bottleneck between the nodes and the parameter server. A popular solution in the literature is to allow each node to do several local updates on the model in each iteration before sending it back to the PS. While this mitigates the communication bottleneck, the statistical heterogeneity of the data owned by the different nodes has proven to delay convergence and bias the model. In this work, we study random walk (RW) learning algorithms for tackling the communication and data heterogeneity problems. The main idea is to leverage available direct connections among the nodes themselves, which are typically "cheaper" than the communication to the PS. In a random walk, the model is thought of as a "baton" that is passed from a node to one of its neighbors after being updated in each iteration. The challenge in designing the RW is the data heterogeneity and the uncertainty about the data distributions. Ideally, we would want to visit more often nodes that hold more informative data. We cast this problem as a sleeping multi-armed bandit (MAB) to design a near-optimal node sampling strategy that achieves variance-reduced gradient estimates and approaches sub-linearly the optimal sampling strategy. Based on this framework, we present an adaptive random walk learning algorithm. We provide theoretical guarantees on its convergence. Our numerical results validate our theoretical findings and show that our algorithm outperforms existing random walk algorithms.

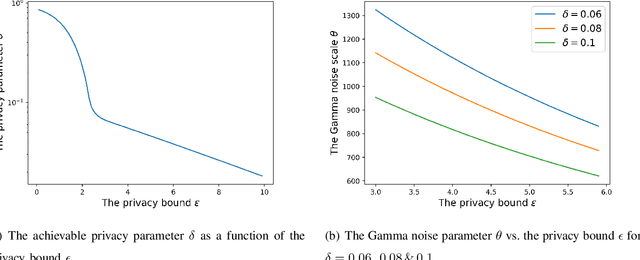
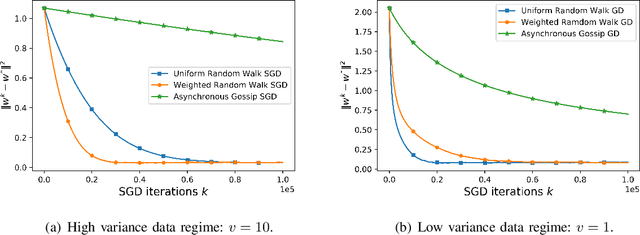
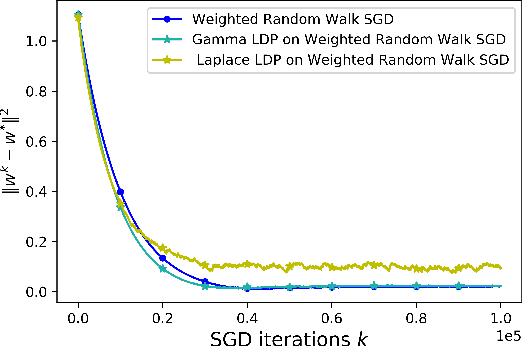
Private Weighted Random Walk Stochastic Gradient Descent

We consider a decentralized learning setting in which data is distributed over nodes in a graph. The goal is to learn a global model on the distributed data without involving any central entity that needs to be trusted. While gossip-based stochastic gradient descent (SGD) can be used to achieve this learning objective, it incurs high communication and computation costs, since it has to wait for all the local models at all the nodes to converge. To speed up the convergence, we propose instead to study random walk based SGD in which a global model is updated based on a random walk on the graph. We propose two algorithms based on two types of random walks that achieve, in a decentralized way, uniform sampling and importance sampling of the data. We provide a non-asymptotic analysis on the rate of convergence, taking into account the constants related to the data and the graph. Our numerical results show that the weighted random walk based algorithm has a better performance for high-variance data. Moreover, we propose a privacy-preserving random walk algorithm that achieves local differential privacy based on a Gamma noise mechanism that we propose. We also give numerical results on the convergence of this algorithm and show that it outperforms additive Laplace-based privacy mechanisms.