Private Weighted Random Walk Stochastic Gradient Descent
Paper and Code
Sep 03, 2020
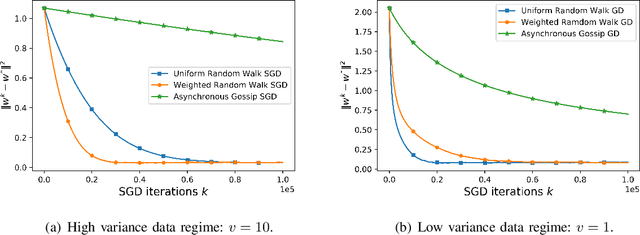
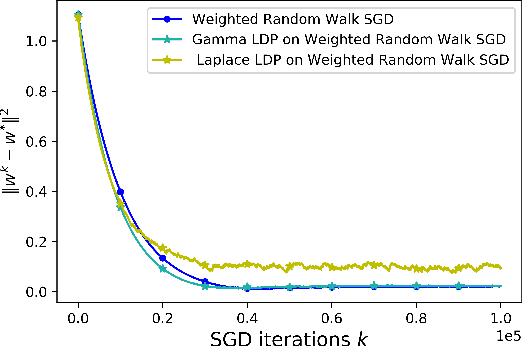
We consider a decentralized learning setting in which data is distributed over nodes in a graph. The goal is to learn a global model on the distributed data without involving any central entity that needs to be trusted. While gossip-based stochastic gradient descent (SGD) can be used to achieve this learning objective, it incurs high communication and computation costs, since it has to wait for all the local models at all the nodes to converge. To speed up the convergence, we propose instead to study random walk based SGD in which a global model is updated based on a random walk on the graph. We propose two algorithms based on two types of random walks that achieve, in a decentralized way, uniform sampling and importance sampling of the data. We provide a non-asymptotic analysis on the rate of convergence, taking into account the constants related to the data and the graph. Our numerical results show that the weighted random walk based algorithm has a better performance for high-variance data. Moreover, we propose a privacy-preserving random walk algorithm that achieves local differential privacy based on a Gamma noise mechanism that we propose. We also give numerical results on the convergence of this algorithm and show that it outperforms additive Laplace-based privacy mechanisms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge