Serge Kas Hanna
Approximate Gradient Coding for Privacy-Flexible Federated Learning with Non-IID Data
Apr 04, 2024Abstract:This work focuses on the challenges of non-IID data and stragglers/dropouts in federated learning. We introduce and explore a privacy-flexible paradigm that models parts of the clients' local data as non-private, offering a more versatile and business-oriented perspective on privacy. Within this framework, we propose a data-driven strategy for mitigating the effects of label heterogeneity and client straggling on federated learning. Our solution combines both offline data sharing and approximate gradient coding techniques. Through numerical simulations using the MNIST dataset, we demonstrate that our approach enables achieving a deliberate trade-off between privacy and utility, leading to improved model convergence and accuracy while using an adaptable portion of non-private data.
Fast and Straggler-Tolerant Distributed SGD with Reduced Computation Load
Apr 17, 2023Abstract:In distributed machine learning, a central node outsources computationally expensive calculations to external worker nodes. The properties of optimization procedures like stochastic gradient descent (SGD) can be leveraged to mitigate the effect of unresponsive or slow workers called stragglers, that otherwise degrade the benefit of outsourcing the computation. This can be done by only waiting for a subset of the workers to finish their computation at each iteration of the algorithm. Previous works proposed to adapt the number of workers to wait for as the algorithm evolves to optimize the speed of convergence. In contrast, we model the communication and computation times using independent random variables. Considering this model, we construct a novel scheme that adapts both the number of workers and the computation load throughout the run-time of the algorithm. Consequently, we improve the convergence speed of distributed SGD while significantly reducing the computation load, at the expense of a slight increase in communication load.
Adaptive Stochastic Gradient Descent for Fast and Communication-Efficient Distributed Learning
Aug 04, 2022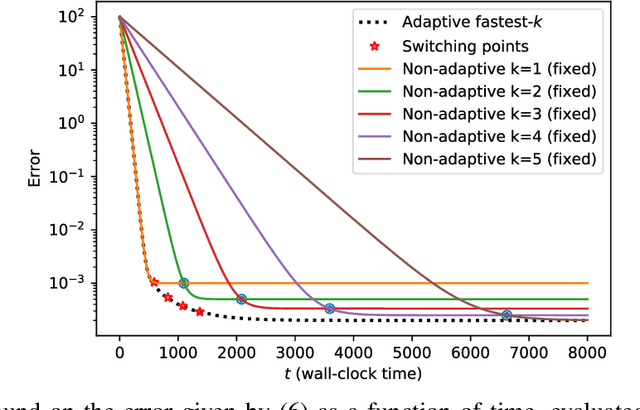
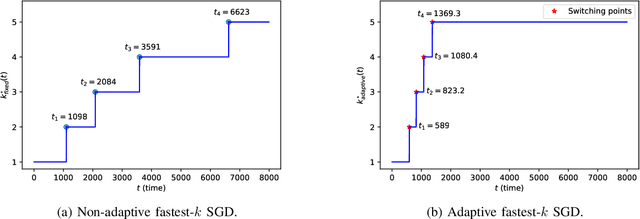
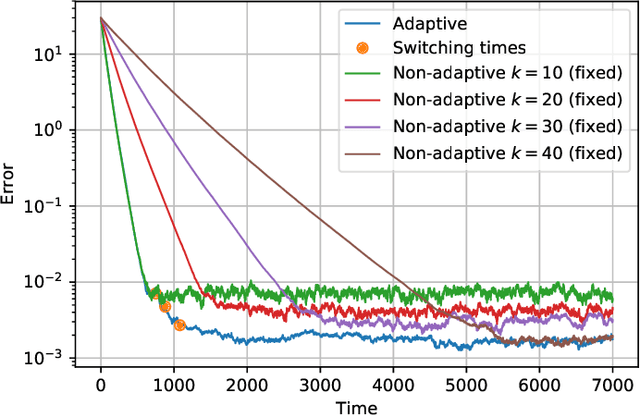
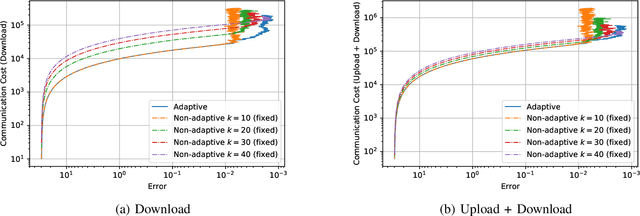
Abstract:We consider the setting where a master wants to run a distributed stochastic gradient descent (SGD) algorithm on $n$ workers, each having a subset of the data. Distributed SGD may suffer from the effect of stragglers, i.e., slow or unresponsive workers who cause delays. One solution studied in the literature is to wait at each iteration for the responses of the fastest $k<n$ workers before updating the model, where $k$ is a fixed parameter. The choice of the value of $k$ presents a trade-off between the runtime (i.e., convergence rate) of SGD and the error of the model. Towards optimizing the error-runtime trade-off, we investigate distributed SGD with adaptive~$k$, i.e., varying $k$ throughout the runtime of the algorithm. We first design an adaptive policy for varying $k$ that optimizes this trade-off based on an upper bound on the error as a function of the wall-clock time that we derive. Then, we propose and implement an algorithm for adaptive distributed SGD that is based on a statistical heuristic. Our results show that the adaptive version of distributed SGD can reach lower error values in less time compared to non-adaptive implementations. Moreover, the results also show that the adaptive version is communication-efficient, where the amount of communication required between the master and the workers is less than that of non-adaptive versions.
Adaptive Distributed Stochastic Gradient Descent for Minimizing Delay in the Presence of Stragglers
Feb 25, 2020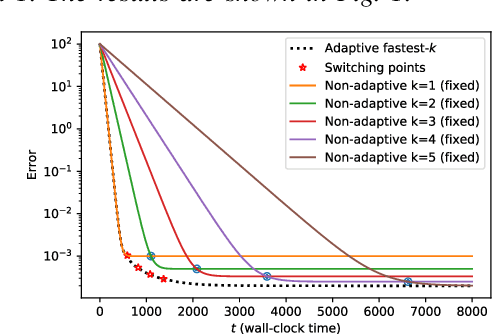
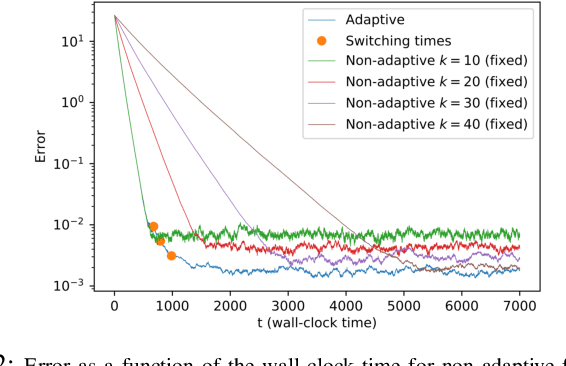
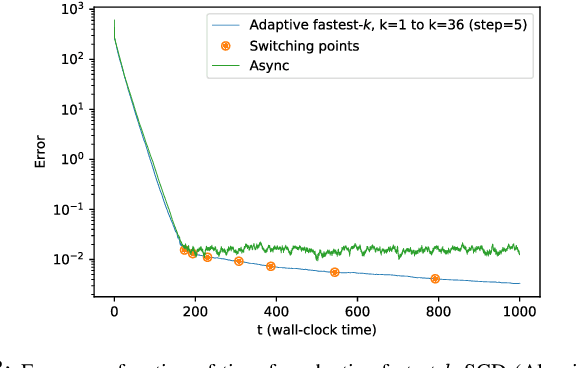
Abstract:We consider the setting where a master wants to run a distributed stochastic gradient descent (SGD) algorithm on $n$ workers each having a subset of the data. Distributed SGD may suffer from the effect of stragglers, i.e., slow or unresponsive workers who cause delays. One solution studied in the literature is to wait at each iteration for the responses of the fastest $k<n$ workers before updating the model, where $k$ is a fixed parameter. The choice of the value of $k$ presents a trade-off between the runtime (i.e., convergence rate) of SGD and the error of the model. Towards optimizing the error-runtime trade-off, we investigate distributed SGD with adaptive $k$. We first design an adaptive policy for varying $k$ that optimizes this trade-off based on an upper bound on the error as a function of the wall-clock time which we derive. Then, we propose an algorithm for adaptive distributed SGD that is based on a statistical heuristic. We implement our algorithm and provide numerical simulations which confirm our intuition and theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge