Decentralized Learning via Random Walk with Jumps

We study decentralized learning over networks where data are distributed across nodes without a central coordinator. Random walk learning is a token-based approach in which a single model is propagated across the network and updated at each visited node using local data, thereby incurring low communication and computational overheads. In weighted random-walk learning, the transition matrix is designed to achieve a desired sampling distribution, thereby speeding up convergence under data heterogeneity. We show that implementing weighted sampling via the Metropolis-Hastings algorithm can lead to a previously unexplored phenomenon we term entrapment. The random walk may become trapped in a small region of the network, resulting in highly correlated updates and severely degraded convergence. To address this issue, we propose Metropolis-Hastings with Levy jumps, which introduces occasional long-range transitions to restore exploration while respecting local information constraints. We establish a convergence rate that explicitly characterizes the roles of data heterogeneity, network spectral gap, and jump probability, and demonstrate through experiments that MHLJ effectively eliminates entrapment and significantly speeds up decentralized learning.

The Entrapment Problem in Random Walk Decentralized Learning

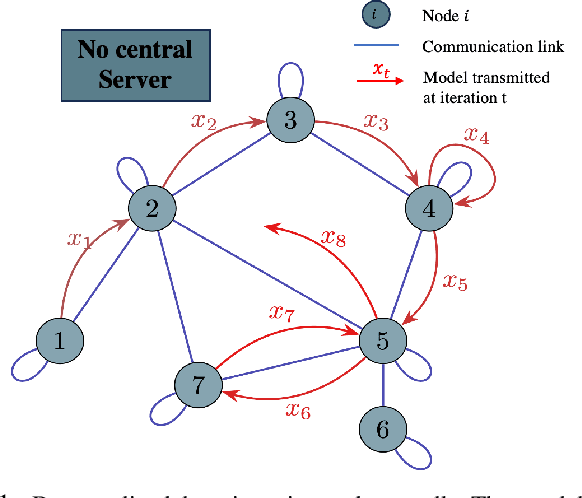
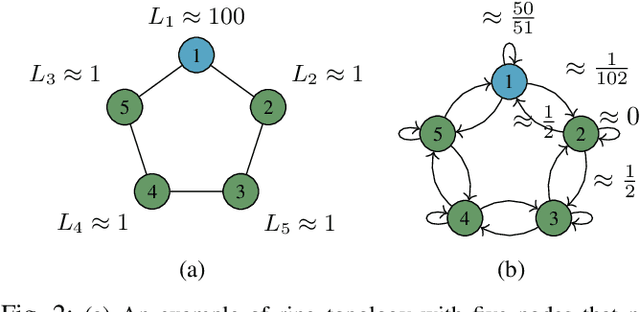
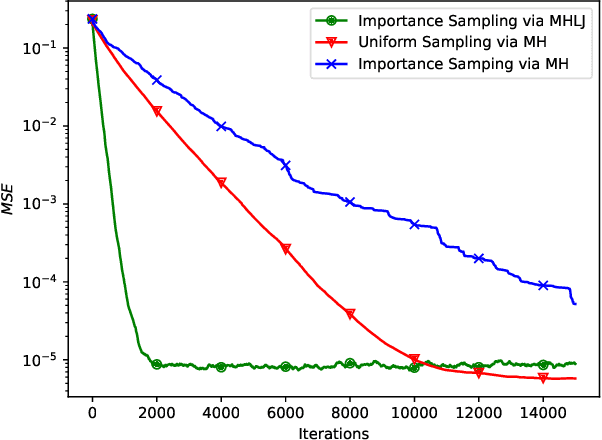
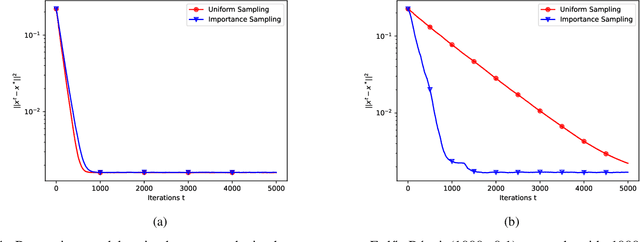
This paper explores decentralized learning in a graph-based setting, where data is distributed across nodes. We investigate a decentralized SGD algorithm that utilizes a random walk to update a global model based on local data. Our focus is on designing the transition probability matrix to speed up convergence. While importance sampling can enhance centralized learning, its decentralized counterpart, using the Metropolis-Hastings (MH) algorithm, can lead to the entrapment problem, where the random walk becomes stuck at certain nodes, slowing convergence. To address this, we propose the Metropolis-Hastings with L\'evy Jumps (MHLJ) algorithm, which incorporates random perturbations (jumps) to overcome entrapment. We theoretically establish the convergence rate and error gap of MHLJ and validate our findings through numerical experiments.