Towards Understanding Text Hallucination of Diffusion Models via Local Generation Bias

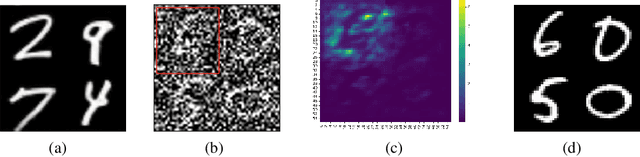
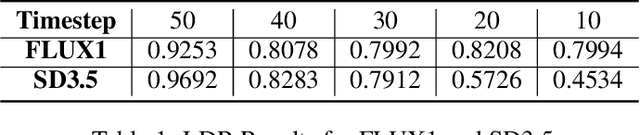
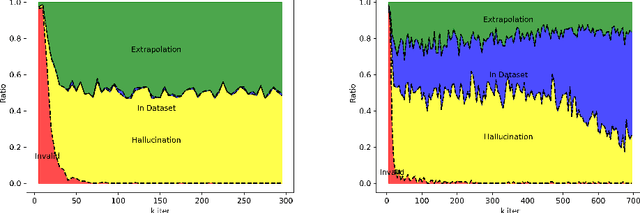
Score-based diffusion models have achieved incredible performance in generating realistic images, audio, and video data. While these models produce high-quality samples with impressive details, they often introduce unrealistic artifacts, such as distorted fingers or hallucinated texts with no meaning. This paper focuses on textual hallucinations, where diffusion models correctly generate individual symbols but assemble them in a nonsensical manner. Through experimental probing, we consistently observe that such phenomenon is attributed it to the network's local generation bias. Denoising networks tend to produce outputs that rely heavily on highly correlated local regions, particularly when different dimensions of the data distribution are nearly pairwise independent. This behavior leads to a generation process that decomposes the global distribution into separate, independent distributions for each symbol, ultimately failing to capture the global structure, including underlying grammar. Intriguingly, this bias persists across various denoising network architectures including MLP and transformers which have the structure to model global dependency. These findings also provide insights into understanding other types of hallucinations, extending beyond text, as a result of implicit biases in the denoising models. Additionally, we theoretically analyze the training dynamics for a specific case involving a two-layer MLP learning parity points on a hypercube, offering an explanation of its underlying mechanism.

MATH-Perturb: Benchmarking LLMs' Math Reasoning Abilities against Hard Perturbations

Large language models have demonstrated impressive performance on challenging mathematical reasoning tasks, which has triggered the discussion of whether the performance is achieved by true reasoning capability or memorization. To investigate this question, prior work has constructed mathematical benchmarks when questions undergo simple perturbations -- modifications that still preserve the underlying reasoning patterns of the solutions. However, no work has explored hard perturbations, which fundamentally change the nature of the problem so that the original solution steps do not apply. To bridge the gap, we construct MATH-P-Simple and MATH-P-Hard via simple perturbation and hard perturbation, respectively. Each consists of 279 perturbed math problems derived from level-5 (hardest) problems in the MATH dataset (Hendrycksmath et. al., 2021). We observe significant performance drops on MATH-P-Hard across various models, including o1-mini (-16.49%) and gemini-2.0-flash-thinking (-12.9%). We also raise concerns about a novel form of memorization where models blindly apply learned problem-solving skills without assessing their applicability to modified contexts. This issue is amplified when using original problems for in-context learning. We call for research efforts to address this challenge, which is critical for developing more robust and reliable reasoning models.

The Marginal Value of Momentum for Small Learning Rate SGD

Momentum is known to accelerate the convergence of gradient descent in strongly convex settings without stochastic gradient noise. In stochastic optimization, such as training neural networks, folklore suggests that momentum may help deep learning optimization by reducing the variance of the stochastic gradient update, but previous theoretical analyses do not find momentum to offer any provable acceleration. Theoretical results in this paper clarify the role of momentum in stochastic settings where the learning rate is small and gradient noise is the dominant source of instability, suggesting that SGD with and without momentum behave similarly in the short and long time horizons. Experiments show that momentum indeed has limited benefits for both optimization and generalization in practical training regimes where the optimal learning rate is not very large, including small- to medium-batch training from scratch on ImageNet and fine-tuning language models on downstream tasks.

Gradient Descent on Two-layer Nets: Margin Maximization and Simplicity Bias

The generalization mystery of overparametrized deep nets has motivated efforts to understand how gradient descent (GD) converges to low-loss solutions that generalize well. Real-life neural networks are initialized from small random values and trained with cross-entropy loss for classification (unlike the "lazy" or "NTK" regime of training where analysis was more successful), and a recent sequence of results (Lyu and Li, 2020; Chizat and Bach, 2020; Ji and Telgarsky, 2020) provide theoretical evidence that GD may converge to the "max-margin" solution with zero loss, which presumably generalizes well. However, the global optimality of margin is proved only in some settings where neural nets are infinitely or exponentially wide. The current paper is able to establish this global optimality for two-layer Leaky ReLU nets trained with gradient flow on linearly separable and symmetric data, regardless of the width. The analysis also gives some theoretical justification for recent empirical findings (Kalimeris et al., 2019) on the so-called simplicity bias of GD towards linear or other "simple" classes of solutions, especially early in training. On the pessimistic side, the paper suggests that such results are fragile. A simple data manipulation can make gradient flow converge to a linear classifier with suboptimal margin.

Going Beyond Linear RL: Sample Efficient Neural Function Approximation

Deep Reinforcement Learning (RL) powered by neural net approximation of the Q function has had enormous empirical success. While the theory of RL has traditionally focused on linear function approximation (or eluder dimension) approaches, little is known about nonlinear RL with neural net approximations of the Q functions. This is the focus of this work, where we study function approximation with two-layer neural networks (considering both ReLU and polynomial activation functions). Our first result is a computationally and statistically efficient algorithm in the generative model setting under completeness for two-layer neural networks. Our second result considers this setting but under only realizability of the neural net function class. Here, assuming deterministic dynamics, the sample complexity scales linearly in the algebraic dimension. In all cases, our results significantly improve upon what can be attained with linear (or eluder dimension) methods.

Optimal Gradient-based Algorithms for Non-concave Bandit Optimization

Bandit problems with linear or concave reward have been extensively studied, but relatively few works have studied bandits with non-concave reward. This work considers a large family of bandit problems where the unknown underlying reward function is non-concave, including the low-rank generalized linear bandit problems and two-layer neural network with polynomial activation bandit problem. For the low-rank generalized linear bandit problem, we provide a minimax-optimal algorithm in the dimension, refuting both conjectures in [LMT21, JWWN19]. Our algorithms are based on a unified zeroth-order optimization paradigm that applies in great generality and attains optimal rates in several structured polynomial settings (in the dimension). We further demonstrate the applicability of our algorithms in RL in the generative model setting, resulting in improved sample complexity over prior approaches. Finally, we show that the standard optimistic algorithms (e.g., UCB) are sub-optimal by dimension factors. In the neural net setting (with polynomial activation functions) with noiseless reward, we provide a bandit algorithm with sample complexity equal to the intrinsic algebraic dimension. Again, we show that optimistic approaches have worse sample complexity, polynomial in the extrinsic dimension (which could be exponentially worse in the polynomial degree).

Mildly Overparametrized Neural Nets can Memorize Training Data Efficiently

It has been observed \citep{zhang2016understanding} that deep neural networks can memorize: they achieve 100\% accuracy on training data. Recent theoretical results explained such behavior in highly overparametrized regimes, where the number of neurons in each layer is larger than the number of training samples. In this paper, we show that neural networks can be trained to memorize training data perfectly in a mildly overparametrized regime, where the number of parameters is just a constant factor more than the number of training samples, and the number of neurons is much smaller.