Multi-Modal Conformal Prediction Regions by Optimizing Convex Shape Templates

Conformal prediction is a statistical tool for producing prediction regions for machine learning models that are valid with high probability. A key component of conformal prediction algorithms is a non-conformity score function that quantifies how different a model's prediction is from the unknown ground truth value. Essentially, these functions determine the shape and the size of the conformal prediction regions. However, little work has gone into finding non-conformity score functions that produce prediction regions that are multi-modal and practical, i.e., that can efficiently be used in engineering applications. We propose a method that optimizes parameterized shape template functions over calibration data, which results in non-conformity score functions that produce prediction regions with minimum volume. Our approach results in prediction regions that are multi-modal, so they can properly capture residuals of distributions that have multiple modes, and practical, so each region is convex and can be easily incorporated into downstream tasks, such as a motion planner using conformal prediction regions. Our method applies to general supervised learning tasks, while we illustrate its use in time-series prediction. We provide a toolbox and present illustrative case studies of F16 fighter jets and autonomous vehicles, showing an up to $68\%$ reduction in prediction region area.

Distributionally Robust Statistical Verification with Imprecise Neural Networks

A particularly challenging problem in AI safety is providing guarantees on the behavior of high-dimensional autonomous systems. Verification approaches centered around reachability analysis fail to scale, and purely statistical approaches are constrained by the distributional assumptions about the sampling process. Instead, we pose a distributionally robust version of the statistical verification problem for black-box systems, where our performance guarantees hold over a large family of distributions. This paper proposes a novel approach based on a combination of active learning, uncertainty quantification, and neural network verification. A central piece of our approach is an ensemble technique called Imprecise Neural Networks, which provides the uncertainty to guide active learning. The active learning uses an exhaustive neural-network verification tool Sherlock to collect samples. An evaluation on multiple physical simulators in the openAI gym Mujoco environments with reinforcement-learned controllers demonstrates that our approach can provide useful and scalable guarantees for high-dimensional systems.

Causal Repair of Learning-enabled Cyber-physical Systems

Models of actual causality leverage domain knowledge to generate convincing diagnoses of events that caused an outcome. It is promising to apply these models to diagnose and repair run-time property violations in cyber-physical systems (CPS) with learning-enabled components (LEC). However, given the high diversity and complexity of LECs, it is challenging to encode domain knowledge (e.g., the CPS dynamics) in a scalable actual causality model that could generate useful repair suggestions. In this paper, we focus causal diagnosis on the input/output behaviors of LECs. Specifically, we aim to identify which subset of I/O behaviors of the LEC is an actual cause for a property violation. An important by-product is a counterfactual version of the LEC that repairs the run-time property by fixing the identified problematic behaviors. Based on this insights, we design a two-step diagnostic pipeline: (1) construct and Halpern-Pearl causality model that reflects the dependency of property outcome on the component's I/O behaviors, and (2) perform a search for an actual cause and corresponding repair on the model. We prove that our pipeline has the following guarantee: if an actual cause is found, the system is guaranteed to be repaired; otherwise, we have high probabilistic confidence that the LEC under analysis did not cause the property violation. We demonstrate that our approach successfully repairs learned controllers on a standard OpenAI Gym benchmark.

Conformal Prediction Regions for Time Series using Linear Complementarity Programming

Conformal prediction is a statistical tool for producing prediction regions of machine learning models that are valid with high probability. However, applying conformal prediction to time series data leads to conservative prediction regions. In fact, to obtain prediction regions over $T$ time steps with confidence $1-\delta$, {previous works require that each individual prediction region is valid} with confidence $1-\delta/T$. We propose an optimization-based method for reducing this conservatism to enable long horizon planning and verification when using learning-enabled time series predictors. Instead of considering prediction errors individually at each time step, we consider a parameterized prediction error over multiple time steps. By optimizing the parameters over an additional dataset, we find prediction regions that are not conservative. We show that this problem can be cast as a mixed integer linear complementarity program (MILCP), which we then relax into a linear complementarity program (LCP). Additionally, we prove that the relaxed LP has the same optimal cost as the original MILCP. Finally, we demonstrate the efficacy of our method on a case study using pedestrian trajectory predictors.

Adaptive Conformal Prediction for Motion Planning among Dynamic Agents

This paper proposes an algorithm for motion planning among dynamic agents using adaptive conformal prediction. We consider a deterministic control system and use trajectory predictors to predict the dynamic agents' future motion, which is assumed to follow an unknown distribution. We then leverage ideas from adaptive conformal prediction to dynamically quantify prediction uncertainty from an online data stream. Particularly, we provide an online algorithm uses delayed agent observations to obtain uncertainty sets for multistep-ahead predictions with probabilistic coverage. These uncertainty sets are used within a model predictive controller to safely navigate among dynamic agents. While most existing data-driven prediction approached quantify prediction uncertainty heuristically, we quantify the true prediction uncertainty in a distribution-free, adaptive manner that even allows to capture changes in prediction quality and the agents' motion. We empirically evaluate of our algorithm on a simulation case studies where a drone avoids a flying frisbee.

Safe Planning in Dynamic Environments using Conformal Prediction

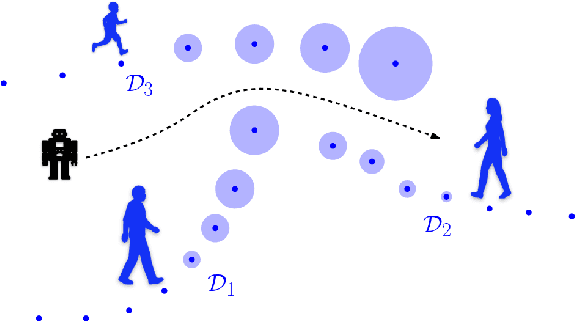
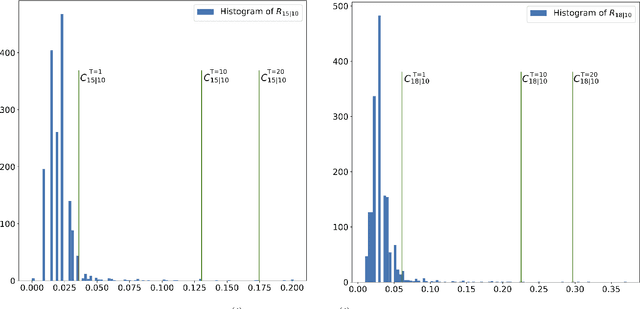
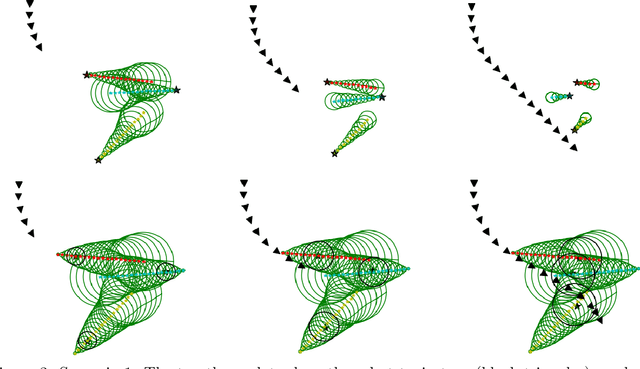
We propose a framework for planning in unknown dynamic environments with probabilistic safety guarantees using conformal prediction. Particularly, we design a model predictive controller (MPC) that uses i) trajectory predictions of the dynamic environment, and ii) prediction regions quantifying the uncertainty of the predictions. To obtain prediction regions, we use conformal prediction, a statistical tool for uncertainty quantification, that requires availability of offline trajectory data - a reasonable assumption in many applications such as autonomous driving. The prediction regions are valid, i.e., they hold with a user-defined probability, so that the MPC is provably safe. We illustrate the results in the self-driving car simulator CARLA at a pedestrian-filled intersection. The strength of our approach is compatibility with state of the art trajectory predictors, e.g., RNNs and LSTMs, while making no assumptions on the underlying trajectory-generating distribution. To the best of our knowledge, these are the first results that provide valid safety guarantees in such a setting.

Learning Enabled Fast Planning and Control in Dynamic Environments with Intermittent Information

This paper addresses a safe planning and control problem for mobile robots operating in communication- and sensor-limited dynamic environments. In this case the robots cannot sense the objects around them and must instead rely on intermittent, external information about the environment, as e.g., in underwater applications. The challenge in this case is that the robots must plan using only this stale data, while accounting for any noise in the data or uncertainty in the environment. To address this challenge we propose a compositional technique which leverages neural networks to quickly plan and control a robot through crowded and dynamic environments using only intermittent information. Specifically, our tool uses reachability analysis and potential fields to train a neural network that is capable of generating safe control actions. We demonstrate our technique both in simulation with an underwater vehicle crossing a crowded shipping channel and with real experiments with ground vehicles in communication- and sensor-limited environments.

Confidence Composition for Monitors of Verification Assumptions

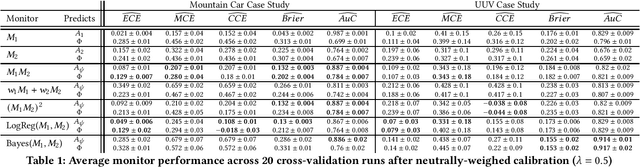
Closed-loop verification of cyber-physical systems with neural network controllers offers strong safety guarantees under certain assumptions. It is, however, difficult to determine whether these guarantees apply at run time because verification assumptions may be violated. To predict safety violations in a verified system, we propose a three-step framework for monitoring the confidence in verification assumptions. First, we represent the sufficient condition for verified safety with a propositional logical formula over assumptions. Second, we build calibrated confidence monitors that evaluate the probability that each assumption holds. Third, we obtain the confidence in the verification guarantees by composing the assumption monitors using a composition function suitable for the logical formula. Our framework provides theoretical bounds on the calibration and conservatism of compositional monitors. In two case studies, we demonstrate that the composed monitors improve over their constituents and successfully predict safety violations.

Robust Motion Planning in the Presence of Estimation Uncertainty

Motion planning is a fundamental problem and focuses on finding control inputs that enable a robot to reach a goal region while safely avoiding obstacles. However, in many situations, the state of the system may not be known but only estimated using, for instance, a Kalman filter. This results in a novel motion planning problem where safety must be ensured in the presence of state estimation uncertainty. Previous approaches to this problem are either conservative or integrate state estimates optimistically which leads to non-robust solutions. Optimistic solutions require frequent replanning to not endanger the safety of the system. We propose a new formulation to this problem with the aim to be robust to state estimation errors while not being overly conservative. In particular, we formulate a stochastic optimal control problem that contains robustified risk-aware safety constraints by incorporating robustness margins to account for state estimation errors. We propose a novel sampling-based approach that builds trees exploring the reachable space of Gaussian distributions that capture uncertainty both in state estimation and in future measurements. We provide robustness guarantees and show, both in theory and simulations, that the induced robustness margins constitute a trade-off between conservatism and robustness for planning under estimation uncertainty that allows to control the frequency of replanning.