Mitigating Downstream Model Risks via Model Provenance

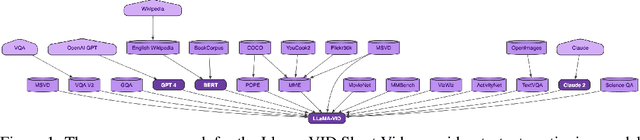
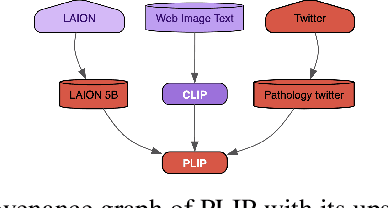
Research and industry are rapidly advancing the innovation and adoption of foundation model-based systems, yet the tools for managing these models have not kept pace. Understanding the provenance and lineage of models is critical for researchers, industry, regulators, and public trust. While model cards and system cards were designed to provide transparency, they fall short in key areas: tracing model genealogy, enabling machine readability, offering reliable centralized management systems, and fostering consistent creation incentives. This challenge mirrors issues in software supply chain security, but AI/ML remains at an earlier stage of maturity. Addressing these gaps requires industry-standard tooling that can be adopted by foundation model publishers, open-source model innovators, and major distribution platforms. We propose a machine-readable model specification format to simplify the creation of model records, thereby reducing error-prone human effort, notably when a new model inherits most of its design from a foundation model. Our solution explicitly traces relationships between upstream and downstream models, enhancing transparency and traceability across the model lifecycle. To facilitate the adoption, we introduce the unified model record (UMR) repository , a semantically versioned system that automates the publication of model records to multiple formats (PDF, HTML, LaTeX) and provides a hosted web interface (https://modelrecord.com/). This proof of concept aims to set a new standard for managing foundation models, bridging the gap between innovation and responsible model management.

Can Large Language Models Understand DL-Lite Ontologies? An Empirical Study

Large language models (LLMs) have shown significant achievements in solving a wide range of tasks. Recently, LLMs' capability to store, retrieve and infer with symbolic knowledge has drawn a great deal of attention, showing their potential to understand structured information. However, it is not yet known whether LLMs can understand Description Logic (DL) ontologies. In this work, we empirically analyze the LLMs' capability of understanding DL-Lite ontologies covering 6 representative tasks from syntactic and semantic aspects. With extensive experiments, we demonstrate both the effectiveness and limitations of LLMs in understanding DL-Lite ontologies. We find that LLMs can understand formal syntax and model-theoretic semantics of concepts and roles. However, LLMs struggle with understanding TBox NI transitivity and handling ontologies with large ABoxes. We hope that our experiments and analyses provide more insights into LLMs and inspire to build more faithful knowledge engineering solutions.

A Short Review for Ontology Learning from Text: Stride from Shallow Learning, Deep Learning to Large Language Models Trend

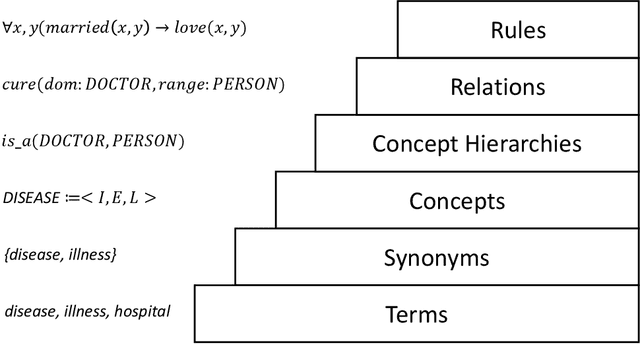
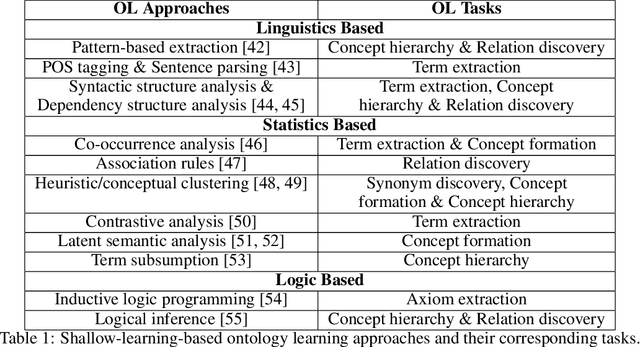
Ontologies provide formal representation of knowledge shared within Semantic Web applications and Ontology learning from text involves the construction of ontologies from a given corpus of text. In the past years, ontology learning has traversed through shallow learning and deep learning methodologies, each offering distinct advantages and limitations in the quest for knowledge extraction and representation. A new trend of these approaches is relying on large language models to enhance ontology learning. This paper gives a review in approaches and challenges of ontology learning. It analyzes the methodologies and limitations of shallow-learning-based and deep-learning-based techniques for ontology learning, and provides comprehensive knowledge for the frontier work of using large language models to enhance ontology learning. In addition, it proposes several noteworthy future directions for further exploration into the integration of large language models with ontology learning tasks.

Embedding Ontologies via Incoprorating Extensional and Intensional Knowledge

Ontologies contain rich knowledge within domain, which can be divided into two categories, namely extensional knowledge and intensional knowledge. Extensional knowledge provides information about the concrete instances that belong to specific concepts in the ontology, while intensional knowledge details inherent properties, characteristics, and semantic associations among concepts. However, existing ontology embedding approaches fail to take both extensional knowledge and intensional knowledge into fine consideration simultaneously. In this paper, we propose a novel ontology embedding approach named EIKE (Extensional and Intensional Knowledge Embedding) by representing ontologies in two spaces, called extensional space and intensional space. EIKE presents a unified framework for embedding instances, concepts and their relations in an ontology, applying a geometry-based method to model extensional knowledge and a pretrained language model to model intensional knowledge, which can capture both structure information and textual information. Experimental results show that EIKE significantly outperforms state-of-the-art methods in three datasets for both triple classification and link prediction, indicating that EIKE provides a more comprehensive and representative perspective of the domain.

An Embedding-based Approach to Inconsistency-tolerant Reasoning with Inconsistent Ontologies

Inconsistency handling is an important issue in knowledge management. Especially in ontology engineering, logical inconsistencies may occur during ontology construction. A natural way to reason with an inconsistent ontology is to utilize the maximal consistent subsets of the ontology. However, previous studies on selecting maximum consistent subsets have rarely considered the semantics of the axioms, which may result in irrational inference. In this paper, we propose a novel approach to reasoning with inconsistent ontologies in description logics based on the embeddings of axioms. We first give a method for turning axioms into distributed semantic vectors to compute the semantic connections between the axioms. We then define an embedding-based method for selecting the maximum consistent subsets and use it to define an inconsistency-tolerant inference relation. We show the rationality of our inference relation by considering some logical properties. Finally, we conduct experiments on several ontologies to evaluate the reasoning power of our inference relation. The experimental results show that our embedding-based method can outperform existing inconsistency-tolerant reasoning methods based on maximal consistent subsets.