OpenHumanVid: A Large-Scale High-Quality Dataset for Enhancing Human-Centric Video Generation

Recent advancements in visual generation technologies have markedly increased the scale and availability of video datasets, which are crucial for training effective video generation models. However, a significant lack of high-quality, human-centric video datasets presents a challenge to progress in this field. To bridge this gap, we introduce OpenHumanVid, a large-scale and high-quality human-centric video dataset characterized by precise and detailed captions that encompass both human appearance and motion states, along with supplementary human motion conditions, including skeleton sequences and speech audio. To validate the efficacy of this dataset and the associated training strategies, we propose an extension of existing classical diffusion transformer architectures and conduct further pretraining of our models on the proposed dataset. Our findings yield two critical insights: First, the incorporation of a large-scale, high-quality dataset substantially enhances evaluation metrics for generated human videos while preserving performance in general video generation tasks. Second, the effective alignment of text with human appearance, human motion, and facial motion is essential for producing high-quality video outputs. Based on these insights and corresponding methodologies, the straightforward extended network trained on the proposed dataset demonstrates an obvious improvement in the generation of human-centric videos. Project page https://fudan-generative-vision.github.io/OpenHumanVid

Ontology Revision based on Pre-trained Language Models

Ontology revision aims to seamlessly incorporate new information into an existing ontology and plays a crucial role in tasks such as ontology evolution, ontology maintenance, and ontology alignment. Similar to repair single ontologies, resolving logical incoherence in the task of ontology revision is also important and meaningful since incoherence is a main potential factor to cause inconsistency and reasoning with an inconsistent ontology will obtain meaningless answers. To deal with this problem, various ontology revision methods have been proposed to define revision operators and design ranking strategies for axioms in an ontology. However, they rarely consider axiom semantics which provides important information to differentiate axioms. On the other hand, pre-trained models can be utilized to encode axiom semantics, and have been widely applied in many natural language processing tasks and ontology-related ones in recent years. Therefore, in this paper, we define four scoring functions to rank axioms based on a pre-trained model by considering various information from a rebuttal ontology and its corresponding reliable ontology. Based on such a scoring function, we propose an ontology revision algorithm to deal with unsatisfiable concepts at once. If it is hard to resolve all unsatisfiable concepts in a rebuttal ontology together, an adapted revision algorithm is designed to deal with them group by group. We conduct experiments over 19 ontology pairs and compare our algorithms and scoring functions with existing ones. According to the experiments, it shows that our algorithms could achieve promising performance. The adapted revision algorithm could improve the efficiency largely, and at most 96% time could be saved for some ontology pairs. Some of our scoring functions help a revision algorithm obtain better results in many cases, especially for the challenging pairs.

An Embedding-based Approach to Inconsistency-tolerant Reasoning with Inconsistent Ontologies

Inconsistency handling is an important issue in knowledge management. Especially in ontology engineering, logical inconsistencies may occur during ontology construction. A natural way to reason with an inconsistent ontology is to utilize the maximal consistent subsets of the ontology. However, previous studies on selecting maximum consistent subsets have rarely considered the semantics of the axioms, which may result in irrational inference. In this paper, we propose a novel approach to reasoning with inconsistent ontologies in description logics based on the embeddings of axioms. We first give a method for turning axioms into distributed semantic vectors to compute the semantic connections between the axioms. We then define an embedding-based method for selecting the maximum consistent subsets and use it to define an inconsistency-tolerant inference relation. We show the rationality of our inference relation by considering some logical properties. Finally, we conduct experiments on several ontologies to evaluate the reasoning power of our inference relation. The experimental results show that our embedding-based method can outperform existing inconsistency-tolerant reasoning methods based on maximal consistent subsets.

Hashing Learning with Hyper-Class Representation

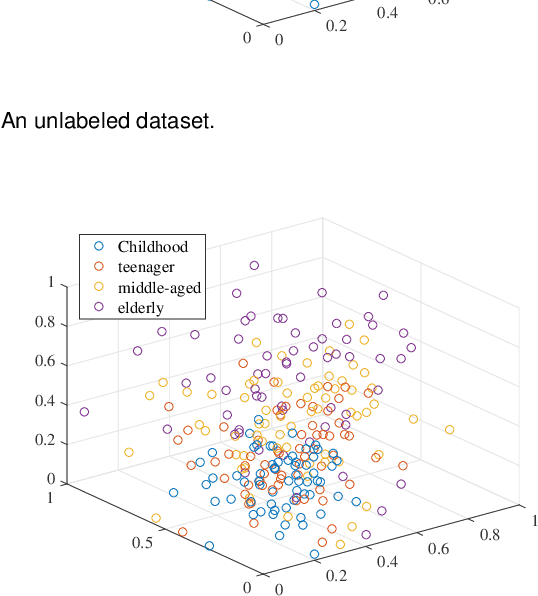
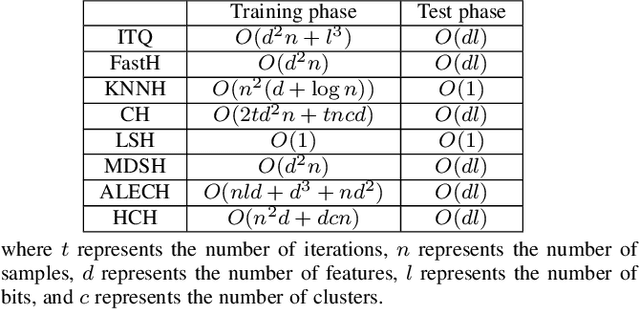
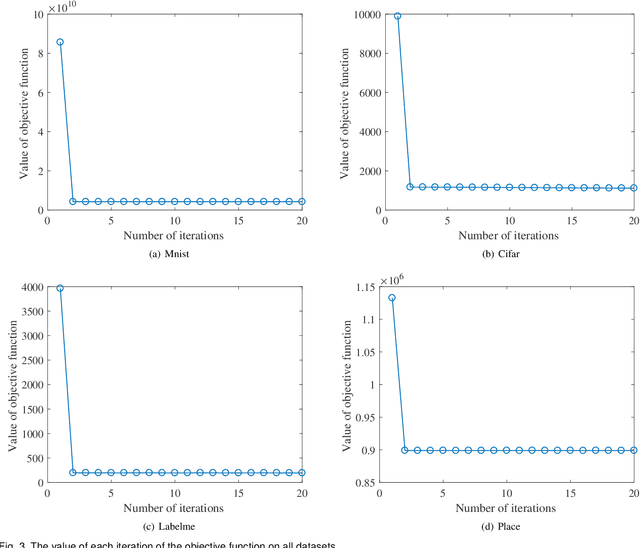
Existing unsupervised hash learning is a kind of attribute-centered calculation. It may not accurately preserve the similarity between data. This leads to low down the performance of hash function learning. In this paper, a hash algorithm is proposed with a hyper-class representation. It is a two-steps approach. The first step finds potential decision features and establish hyper-class. The second step constructs hash learning based on the hyper-class information in the first step, so that the hash codes of the data within the hyper-class are as similar as possible, as well as the hash codes of the data between the hyper-classes are as different as possible. To evaluate the efficiency, a series of experiments are conducted on four public datasets. The experimental results show that the proposed hash algorithm is more efficient than the compared algorithms, in terms of mean average precision (MAP), average precision (AP) and Hamming radius 2 (HAM2)

Hyper-Class Representation of Data

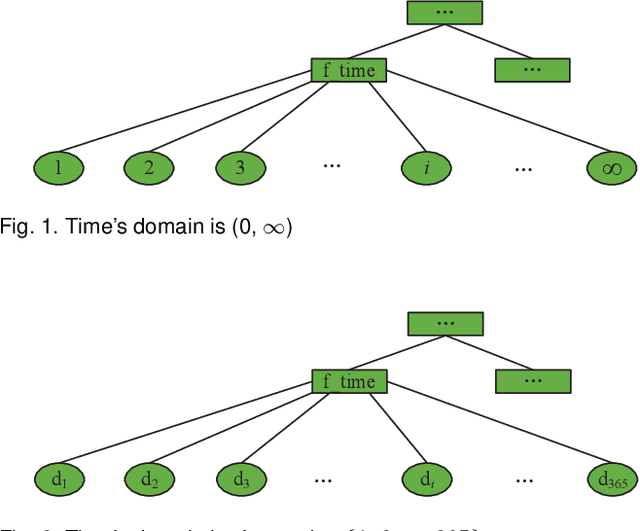
Data representation is often of the natural form with their attribute values. To utilize the data efficiently, one needs to well understand the observed attribute values and identify the potential useful information in the data/smaples, or training data. In this paper, a new data representation, named as hyper-classes representation, is proposed for improving recommendation. At first, the cross entropy, KL divergence and JS divergence of features in data are defined. And then, the hyper-classes in data can be discovered with these three parameters. Finally, a kind of recommendation algorithm is used to evaluate the proposed hyper-class representation of data, and shows that the hyper-class representation is able to provide truly useful reference information for recommendation systems and makes recommendations much better than existing algorithms, i.e., this approach is efficient and promising.

Z Distance Function for KNN Classification

This paper proposes a new distance metric function, called Z distance, for KNN classification. The Z distance function is not a geometric direct-line distance between two data points. It gives a consideration to the class attribute of a training dataset when measuring the affinity between data points. Concretely speaking, the Z distance of two data points includes their class center distance and real distance. And its shape looks like "Z". In this way, the affinity of two data points in the same class is always stronger than that in different classes. Or, the intraclass data points are always closer than those interclass data points. We evaluated the Z distance with experiments, and demonstrated that the proposed distance function achieved better performance in KNN classification.

KNN Classification with One-step Computation

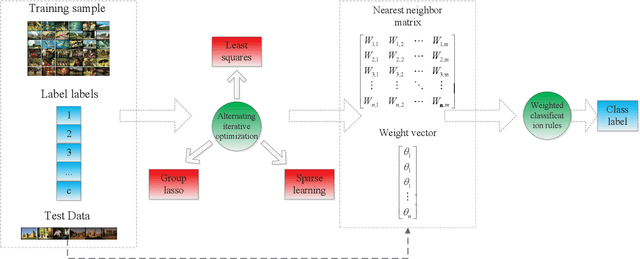
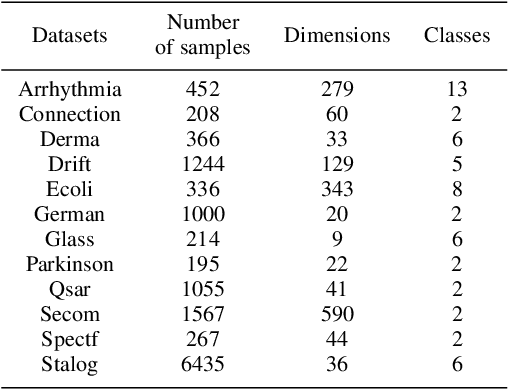
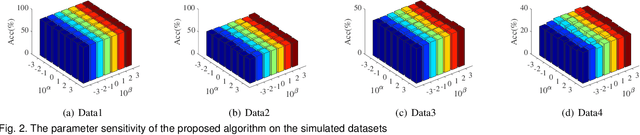
KNN classification is a query triggered yet improvisational learning mode, in which they are carried out only when a test data is predicted that set a suitable K value and search the K nearest neighbors from the whole training sample space, referred them to the lazy part of KNN classification. This lazy part has been the bottleneck problem of applying KNN classification. In this paper, a one-step computation is proposed to replace the lazy part of KNN classification. The one-step computation actually transforms the lazy part to a matrix computation as follows. Given a test data, training samples are first applied to fit the test data with the least squares loss function. And then, a relationship matrix is generated by weighting all training samples according to their influence on the test data. Finally, a group lasso is employed to perform sparse learning of the relationship matrix. In this way, setting K value and searching K nearest neighbors are both integrated to a unified computation. In addition, a new classification rule is proposed for improving the performance of one-step KNN classification. The proposed approach is experimentally evaluated, and demonstrated that the one-step KNN classification is efficient and promising.