Kaili Ma
Measuring and Improving the Use of Graph Information in Graph Neural Networks
Jun 27, 2022
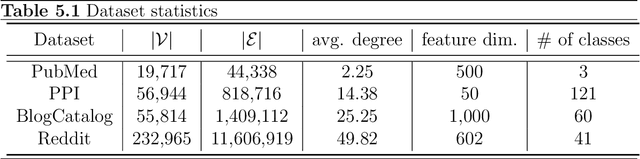
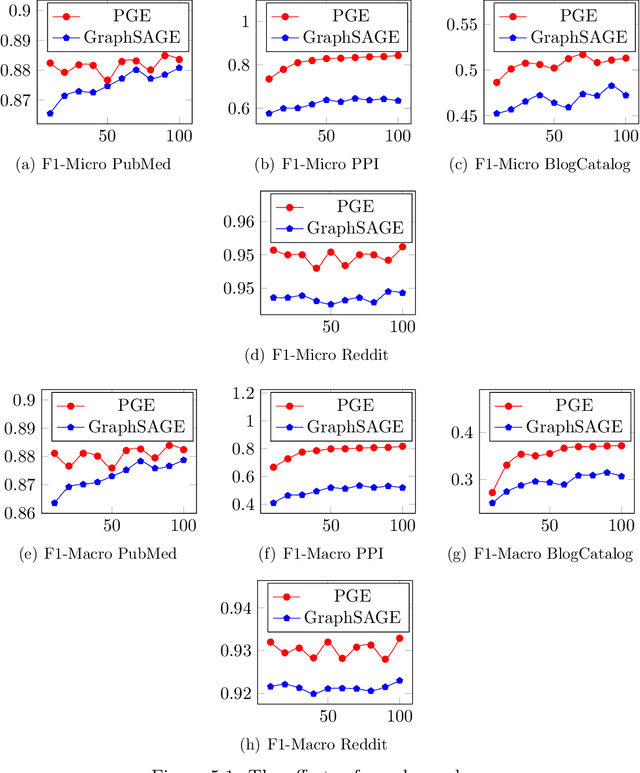
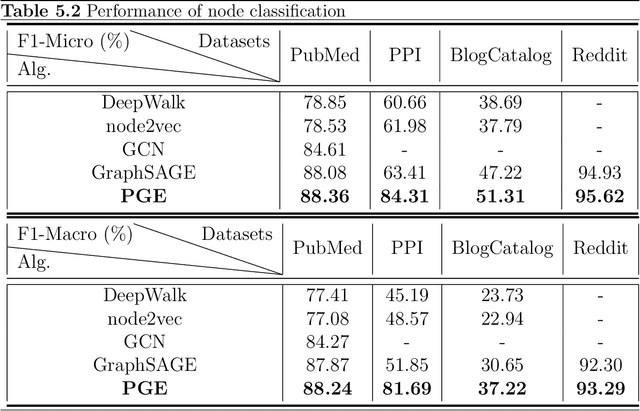
Abstract:Graph neural networks (GNNs) have been widely used for representation learning on graph data. However, there is limited understanding on how much performance GNNs actually gain from graph data. This paper introduces a context-surrounding GNN framework and proposes two smoothness metrics to measure the quantity and quality of information obtained from graph data. A new GNN model, called CS-GNN, is then designed to improve the use of graph information based on the smoothness values of a graph. CS-GNN is shown to achieve better performance than existing methods in different types of real graphs.
Pareto Invariant Risk Minimization
Jun 15, 2022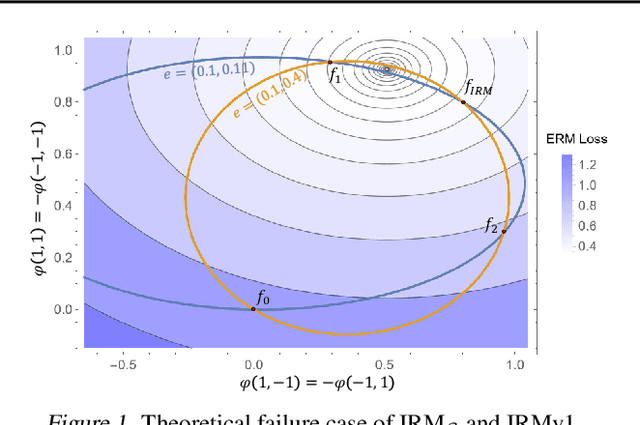
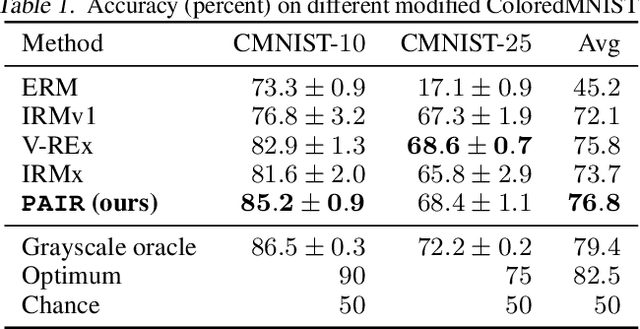
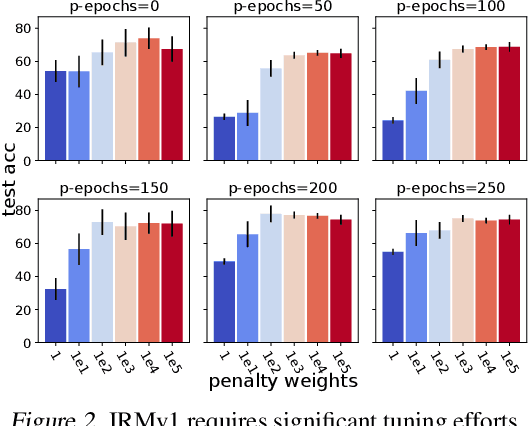
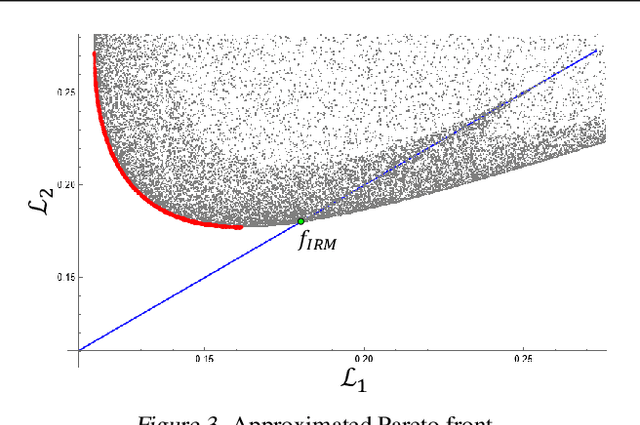
Abstract:Despite the success of invariant risk minimization (IRM) in tackling the Out-of-Distribution generalization problem, IRM can compromise the optimality when applied in practice. The practical variants of IRM, e.g., IRMv1, have been shown to have significant gaps with IRM and thus could fail to capture the invariance even in simple problems. Moreover, the optimization procedure in IRMv1 involves two intrinsically conflicting objectives, and often requires careful tuning for the objective weights. To remedy the above issues, we reformulate IRM as a multi-objective optimization problem, and propose a new optimization scheme for IRM, called PAreto Invariant Risk Minimization (PAIR). PAIR can adaptively adjust the optimization direction under the objective conflicts. Furthermore, we show PAIR can empower the practical IRM variants to overcome the barriers with the original IRM when provided with proper guidance. We conduct experiments with ColoredMNIST to confirm our theory and the effectiveness of PAIR.
Understanding and Improving Graph Injection Attack by Promoting Unnoticeability
Feb 16, 2022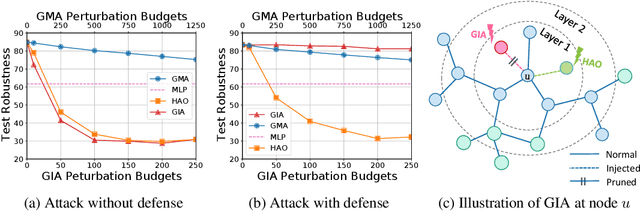
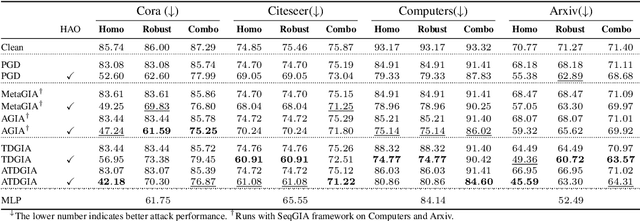
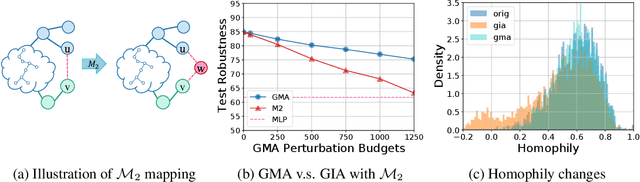
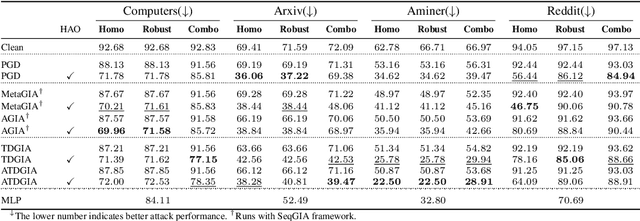
Abstract:Recently Graph Injection Attack (GIA) emerges as a practical attack scenario on Graph Neural Networks (GNNs), where the adversary can merely inject few malicious nodes instead of modifying existing nodes or edges, i.e., Graph Modification Attack (GMA). Although GIA has achieved promising results, little is known about why it is successful and whether there is any pitfall behind the success. To understand the power of GIA, we compare it with GMA and find that GIA can be provably more harmful than GMA due to its relatively high flexibility. However, the high flexibility will also lead to great damage to the homophily distribution of the original graph, i.e., similarity among neighbors. Consequently, the threats of GIA can be easily alleviated or even prevented by homophily-based defenses designed to recover the original homophily. To mitigate the issue, we introduce a novel constraint -- homophily unnoticeability that enforces GIA to preserve the homophily, and propose Harmonious Adversarial Objective (HAO) to instantiate it. Extensive experiments verify that GIA with HAO can break homophily-based defenses and outperform previous GIA attacks by a significant margin. We believe our methods can serve for a more reliable evaluation of the robustness of GNNs.
Invariance Principle Meets Out-of-Distribution Generalization on Graphs
Feb 11, 2022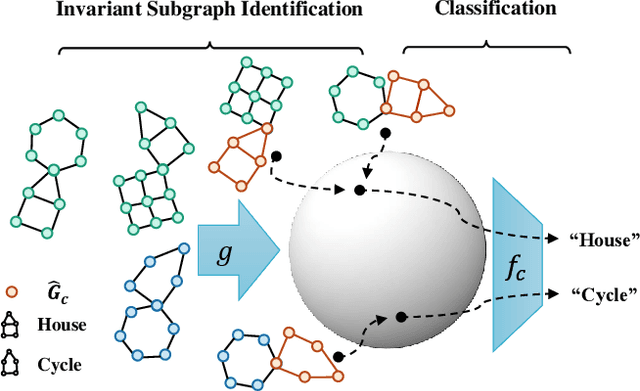

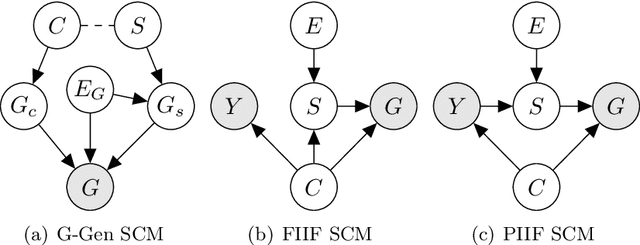
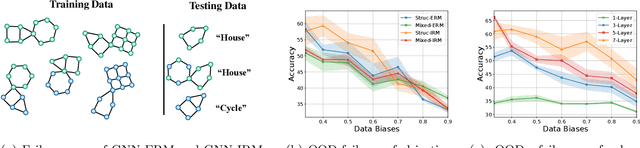
Abstract:Despite recent developments in using the invariance principle from causality to enable out-of-distribution (OOD) generalization on Euclidean data, e.g., images, studies on graph data are limited. Different from images, the complex nature of graphs poses unique challenges that thwart the adoption of the invariance principle for OOD generalization. In particular, distribution shifts on graphs can happen at both structure-level and attribute-level, which increases the difficulty of capturing the invariance. Moreover, domain or environment partitions, which are often required by OOD methods developed on Euclidean data, can be expensive to obtain for graphs. Aiming to bridge this gap, we characterize distribution shifts on graphs with causal models, and show that the OOD generalization on graphs with invariance principle is possible by identifying an invariant subgraph for making predictions. We propose a novel framework to explicitly model this process using a contrastive strategy. By contrasting the estimated invariant subgraphs, our framework can provably identify the underlying invariant subgraph under mild assumptions. Experiments across several synthetic and real-world datasets demonstrate the state-of-the-art OOD generalization ability of our method.
Edge Rewiring Goes Neural: Boosting Network Resilience via Policy Gradient
Oct 18, 2021
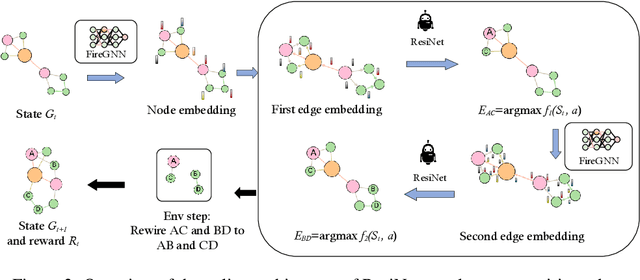
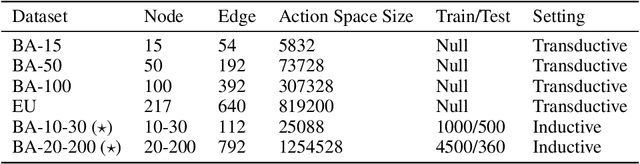
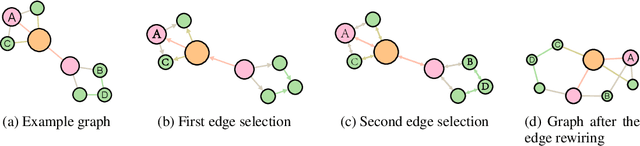
Abstract:Improving the resilience of a network protects the system from natural disasters and malicious attacks. This is typically achieved by introducing new edges, which however may reach beyond the maximum number of connections a node could sustain. Many studies then resort to the degree-preserving operation of rewiring, which swaps existing edges $AC, BD$ to new edges $AB, CD$. A significant line of studies focuses on this technique for theoretical and practical results while leaving three limitations: network utility loss, local optimality, and transductivity. In this paper, we propose ResiNet, a reinforcement learning (RL)-based framework to discover resilient network topologies against various disasters and attacks. ResiNet is objective agnostic which allows the utility to be balanced by incorporating it into the objective function. The local optimality, typically seen in greedy algorithms, is addressed by casting the cumulative resilience gain into a sequential decision process of step-wise rewiring. The transductivity, which refers to the necessity to run a computationally intensive optimization for each input graph, is lifted by our variant of RL with auto-regressive permutation-invariant variable action space. ResiNet is armed by our technical innovation, Filtration enhanced GNN (FireGNN), which distinguishes graphs with minor differences. It is thus possible for ResiNet to capture local structure changes and adapt its decision among consecutive graphs, which is known to be infeasible for GNN. Extensive experiments demonstrate that with a small number of rewiring operations, ResiNet achieves a near-optimal resilience gain on multiple graphs while balancing the utility, with a large margin compared to existing approaches.
Improving Graph Representation Learning by Contrastive Regularization
Jan 27, 2021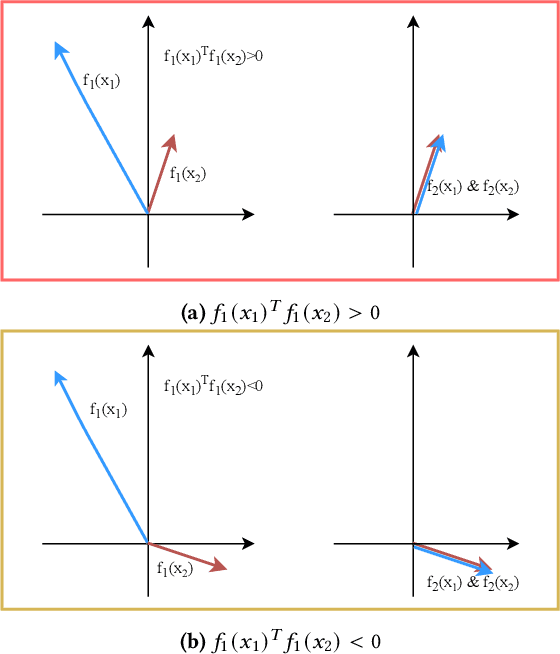
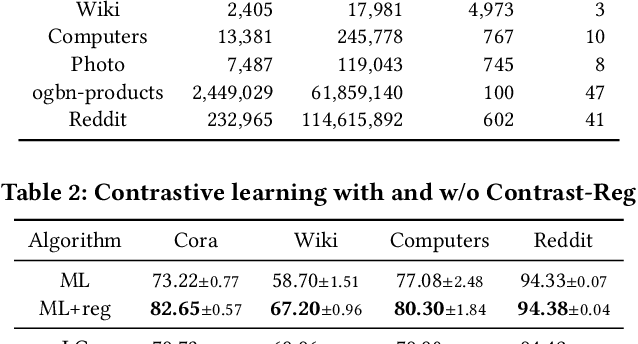
Abstract:Graph representation learning is an important task with applications in various areas such as online social networks, e-commerce networks, WWW, and semantic webs. For unsupervised graph representation learning, many algorithms such as Node2Vec and Graph-SAGE make use of "negative sampling" and/or noise contrastive estimation loss. This bears similar ideas to contrastive learning, which "contrasts" the node representation similarities of semantically similar (positive) pairs against those of negative pairs. However, despite the success of contrastive learning, we found that directly applying this technique to graph representation learning models (e.g., graph convolutional networks) does not always work. We theoretically analyze the generalization performance and propose a light-weight regularization term that avoids the high scales of node representations' norms and the high variance among them to improve the generalization performance. Our experimental results further validate that this regularization term significantly improves the representation quality across different node similarity definitions and outperforms the state-of-the-art methods.
Rethinking Graph Regularization For Graph Neural Networks
Sep 04, 2020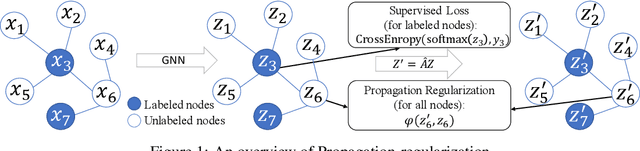
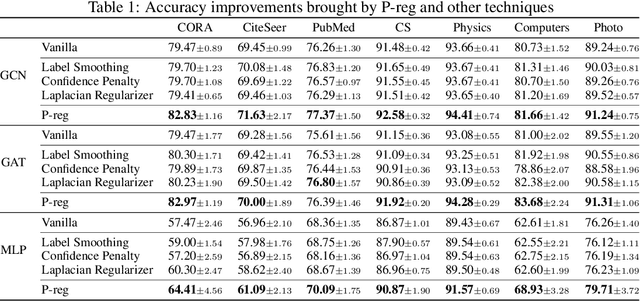
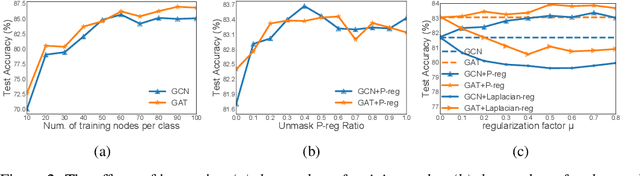
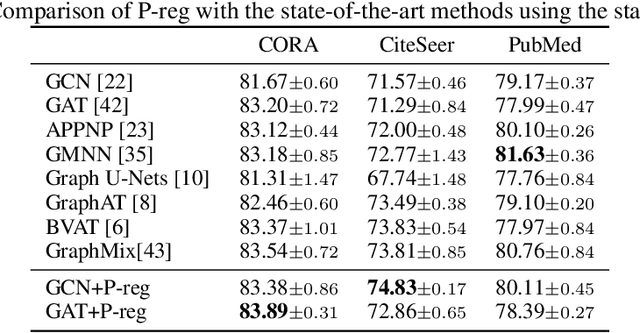
Abstract:The graph Laplacian regularization term is usually used in semi-supervised node classification to provide graph structure information for a model $f(X)$. However, with the recent popularity of graph neural networks (GNNs), directly encoding graph structure $A$ into a model, i.e., $f(A, X)$, has become the more common approach. While we show that graph Laplacian regularization $f(X)^\top \Delta f(X)$ brings little-to-no benefit to existing GNNs, we propose a simple but non-trivial variant of graph Laplacian regularization, called Propagation-regularization (P-reg), to boost the performance of existing GNN models. We provide formal analyses to show that P-reg not only infuses extra information (that is not captured by the traditional graph Laplacian regularization) into GNNs, but also has the capacity equivalent to an infinite-depth graph convolutional network. The code is available at https://github.com/yang-han/P-reg.
Understanding Graph Neural Networks from Graph Signal Denoising Perspectives
Jun 08, 2020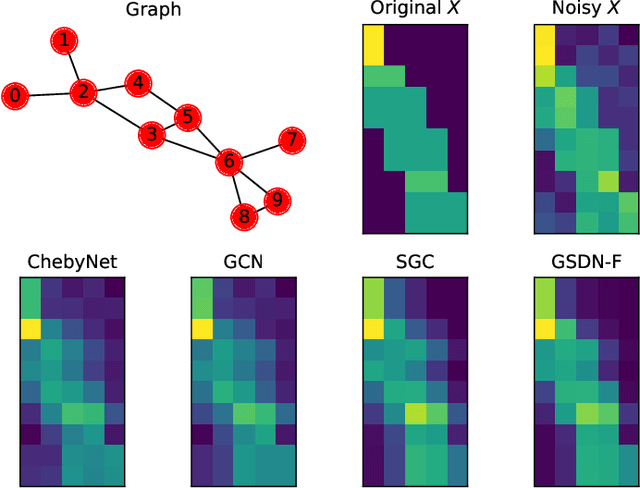
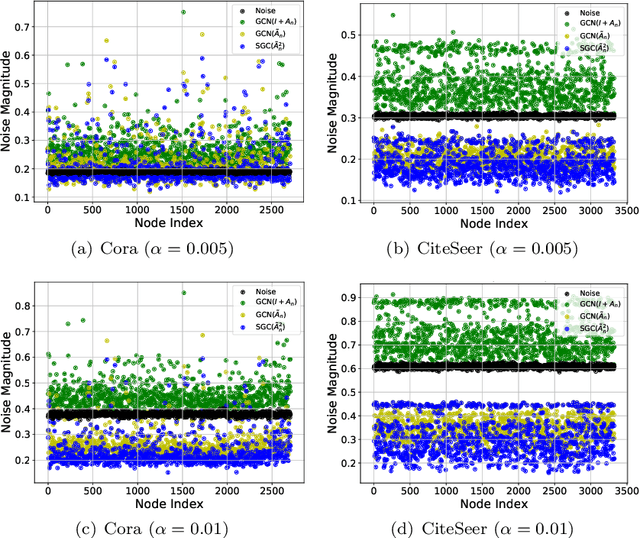
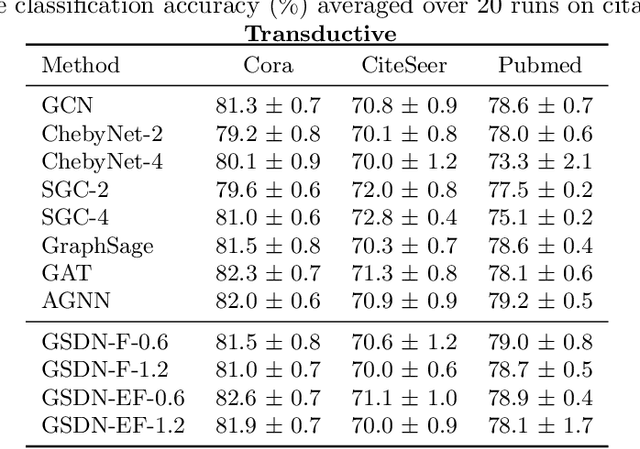
Abstract:Graph neural networks (GNNs) have attracted much attention because of their excellent performance on tasks such as node classification. However, there is inadequate understanding on how and why GNNs work, especially for node representation learning. This paper aims to provide a theoretical framework to understand GNNs, specifically, spectral graph convolutional networks and graph attention networks, from graph signal denoising perspectives. Our framework shows that GNNs are implicitly solving graph signal denoising problems: spectral graph convolutions work as denoising node features, while graph attentions work as denoising edge weights. We also show that a linear self-attention mechanism is able to compete with the state-of-the-art graph attention methods. Our theoretical results further lead to two new models, GSDN-F and GSDN-EF, which work effectively for graphs with noisy node features and/or noisy edges. We validate our theoretical findings and also the effectiveness of our new models by experiments on benchmark datasets. The source code is available at \url{https://github.com/fuguoji/GSDN}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge