Enhancing Neural Subset Selection: Integrating Background Information into Set Representations

Learning neural subset selection tasks, such as compound selection in AI-aided drug discovery, have become increasingly pivotal across diverse applications. The existing methodologies in the field primarily concentrate on constructing models that capture the relationship between utility function values and subsets within their respective supersets. However, these approaches tend to overlook the valuable information contained within the superset when utilizing neural networks to model set functions. In this work, we address this oversight by adopting a probabilistic perspective. Our theoretical findings demonstrate that when the target value is conditioned on both the input set and subset, it is essential to incorporate an \textit{invariant sufficient statistic} of the superset into the subset of interest for effective learning. This ensures that the output value remains invariant to permutations of the subset and its corresponding superset, enabling identification of the specific superset from which the subset originated. Motivated by these insights, we propose a simple yet effective information aggregation module designed to merge the representations of subsets and supersets from a permutation invariance perspective. Comprehensive empirical evaluations across diverse tasks and datasets validate the enhanced efficacy of our approach over conventional methods, underscoring the practicality and potency of our proposed strategies in real-world contexts.

Enhancing Evolving Domain Generalization through Dynamic Latent Representations

Domain generalization is a critical challenge for machine learning systems. Prior domain generalization methods focus on extracting domain-invariant features across several stationary domains to enable generalization to new domains. However, in non-stationary tasks where new domains evolve in an underlying continuous structure, such as time, merely extracting the invariant features is insufficient for generalization to the evolving new domains. Nevertheless, it is non-trivial to learn both evolving and invariant features within a single model due to their conflicts. To bridge this gap, we build causal models to characterize the distribution shifts concerning the two patterns, and propose to learn both dynamic and invariant features via a new framework called Mutual Information-Based Sequential Autoencoders (MISTS). MISTS adopts information theoretic constraints onto sequential autoencoders to disentangle the dynamic and invariant features, and leverage a domain adaptive classifier to make predictions based on both evolving and invariant information. Our experimental results on both synthetic and real-world datasets demonstrate that MISTS succeeds in capturing both evolving and invariant information, and present promising results in evolving domain generalization tasks.

Positional Information Matters for Invariant In-Context Learning: A Case Study of Simple Function Classes

In-context learning (ICL) refers to the ability of a model to condition on a few in-context demonstrations (input-output examples of the underlying task) to generate the answer for a new query input, without updating parameters. Despite the impressive ICL ability of LLMs, it has also been found that ICL in LLMs is sensitive to input demonstrations and limited to short context lengths. To understand the limitations and principles for successful ICL, we conduct an investigation with ICL linear regression of transformers. We characterize several Out-of-Distribution (OOD) cases for ICL inspired by realistic LLM ICL failures and compare transformers with DeepSet, a simple yet powerful architecture for ICL. Surprisingly, DeepSet outperforms transformers across a variety of distribution shifts, implying that preserving permutation invariance symmetry to input demonstrations is crucial for OOD ICL. The phenomenon specifies a fundamental requirement by ICL, which we termed as ICL invariance. Nevertheless, the positional encodings in LLMs will break ICL invariance. To this end, we further evaluate transformers with identical positional encodings and find preserving ICL invariance in transformers achieves state-of-the-art performance across various ICL distribution shifts

Does Invariant Graph Learning via Environment Augmentation Learn Invariance?

Invariant graph representation learning aims to learn the invariance among data from different environments for out-of-distribution generalization on graphs. As the graph environment partitions are usually expensive to obtain, augmenting the environment information has become the de facto approach. However, the usefulness of the augmented environment information has never been verified. In this work, we find that it is fundamentally impossible to learn invariant graph representations via environment augmentation without additional assumptions. Therefore, we develop a set of minimal assumptions, including variation sufficiency and variation consistency, for feasible invariant graph learning. We then propose a new framework Graph invAriant Learning Assistant (GALA). GALA incorporates an assistant model that needs to be sensitive to graph environment changes or distribution shifts. The correctness of the proxy predictions by the assistant model hence can differentiate the variations in spurious subgraphs. We show that extracting the maximally invariant subgraph to the proxy predictions provably identifies the underlying invariant subgraph for successful OOD generalization under the established minimal assumptions. Extensive experiments on datasets including DrugOOD with various graph distribution shifts confirm the effectiveness of GALA.

Pareto Invariant Risk Minimization

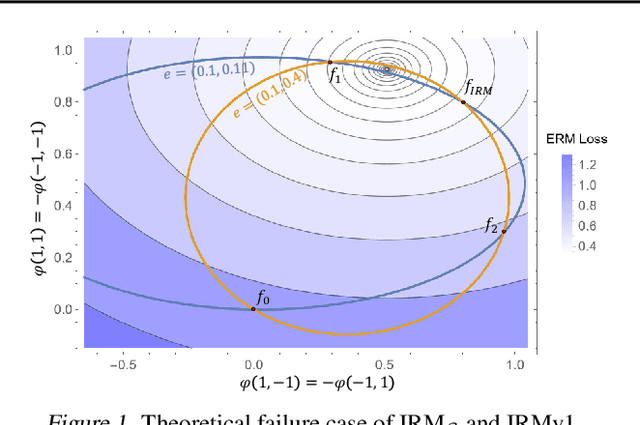
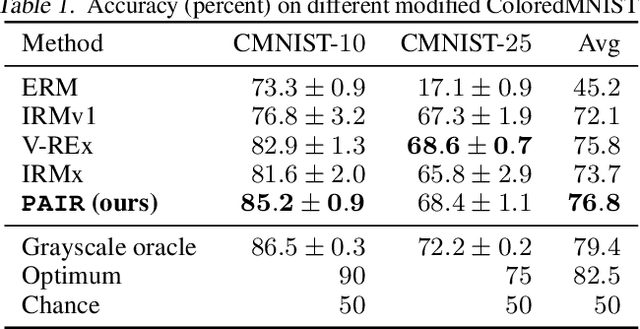
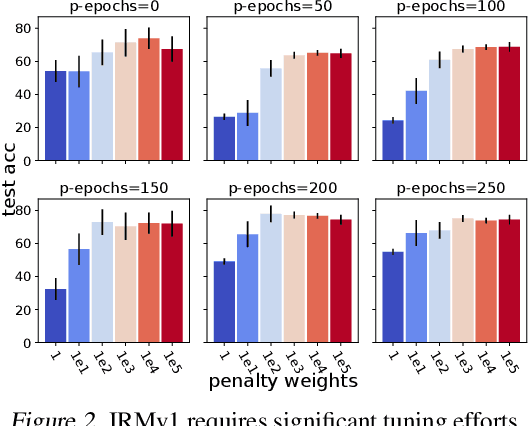
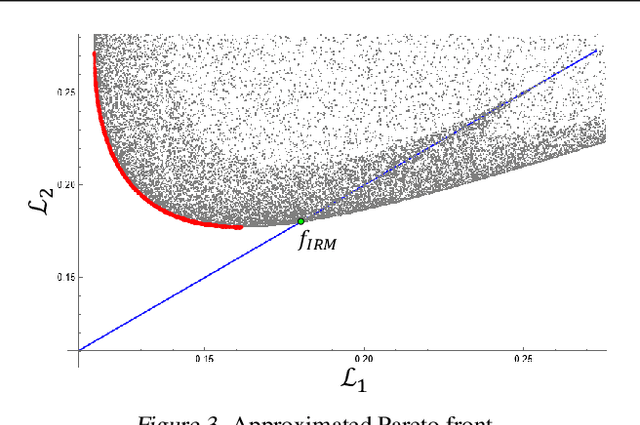
Despite the success of invariant risk minimization (IRM) in tackling the Out-of-Distribution generalization problem, IRM can compromise the optimality when applied in practice. The practical variants of IRM, e.g., IRMv1, have been shown to have significant gaps with IRM and thus could fail to capture the invariance even in simple problems. Moreover, the optimization procedure in IRMv1 involves two intrinsically conflicting objectives, and often requires careful tuning for the objective weights. To remedy the above issues, we reformulate IRM as a multi-objective optimization problem, and propose a new optimization scheme for IRM, called PAreto Invariant Risk Minimization (PAIR). PAIR can adaptively adjust the optimization direction under the objective conflicts. Furthermore, we show PAIR can empower the practical IRM variants to overcome the barriers with the original IRM when provided with proper guidance. We conduct experiments with ColoredMNIST to confirm our theory and the effectiveness of PAIR.

Fast and Reliable Evaluation of Adversarial Robustness with Minimum-Margin Attack

The AutoAttack (AA) has been the most reliable method to evaluate adversarial robustness when considerable computational resources are available. However, the high computational cost (e.g., 100 times more than that of the project gradient descent attack) makes AA infeasible for practitioners with limited computational resources, and also hinders applications of AA in the adversarial training (AT). In this paper, we propose a novel method, minimum-margin (MM) attack, to fast and reliably evaluate adversarial robustness. Compared with AA, our method achieves comparable performance but only costs 3% of the computational time in extensive experiments. The reliability of our method lies in that we evaluate the quality of adversarial examples using the margin between two targets that can precisely identify the most adversarial example. The computational efficiency of our method lies in an effective Sequential TArget Ranking Selection (STARS) method, ensuring that the cost of the MM attack is independent of the number of classes. The MM attack opens a new way for evaluating adversarial robustness and provides a feasible and reliable way to generate high-quality adversarial examples in AT.

An Adaptive Incremental Gradient Method With Support for Non-Euclidean Norms

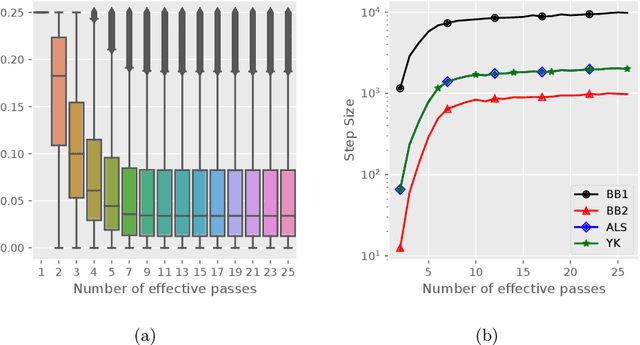
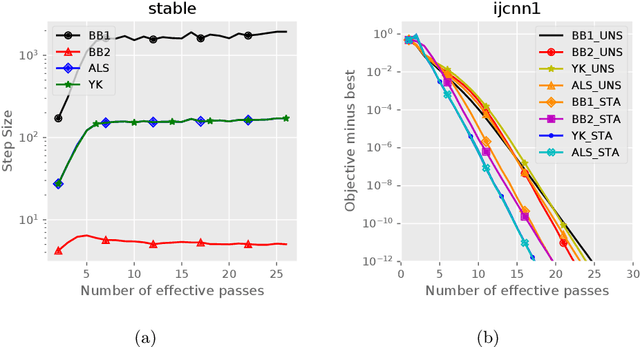
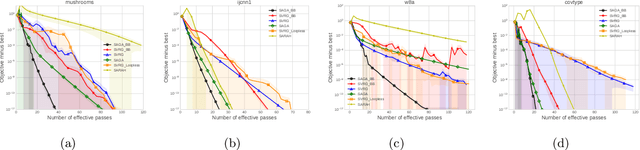
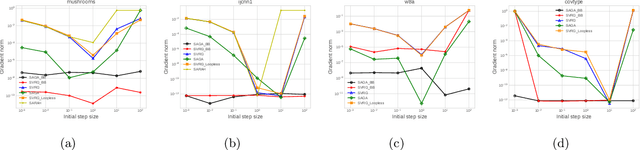
Stochastic variance reduced methods have shown strong performance in solving finite-sum problems. However, these methods usually require the users to manually tune the step-size, which is time-consuming or even infeasible for some large-scale optimization tasks. To overcome the problem, we propose and analyze several novel adaptive variants of the popular SAGA algorithm. Eventually, we design a variant of Barzilai-Borwein step-size which is tailored for the incremental gradient method to ensure memory efficiency and fast convergence. We establish its convergence guarantees under general settings that allow non-Euclidean norms in the definition of smoothness and the composite objectives, which cover a broad range of applications in machine learning. We improve the analysis of SAGA to support non-Euclidean norms, which fills the void of existing work. Numerical experiments on standard datasets demonstrate a competitive performance of the proposed algorithm compared with existing variance-reduced methods and their adaptive variants.

Invariance Principle Meets Out-of-Distribution Generalization on Graphs

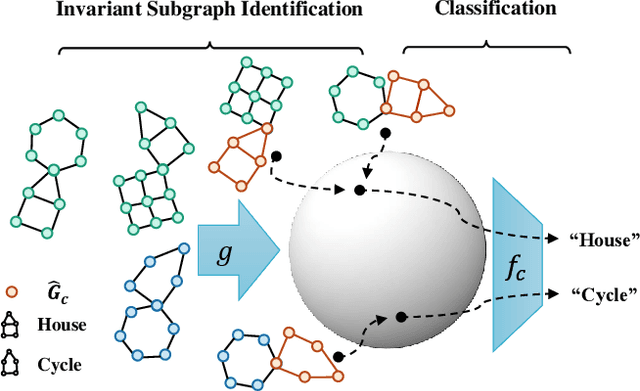
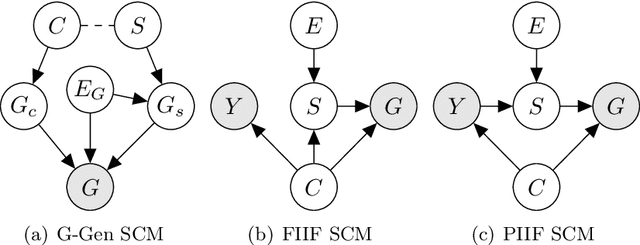
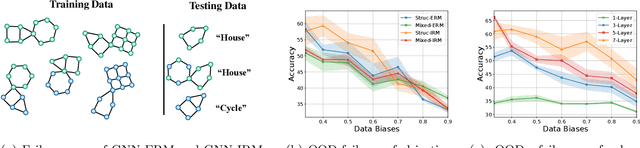
Despite recent developments in using the invariance principle from causality to enable out-of-distribution (OOD) generalization on Euclidean data, e.g., images, studies on graph data are limited. Different from images, the complex nature of graphs poses unique challenges that thwart the adoption of the invariance principle for OOD generalization. In particular, distribution shifts on graphs can happen at both structure-level and attribute-level, which increases the difficulty of capturing the invariance. Moreover, domain or environment partitions, which are often required by OOD methods developed on Euclidean data, can be expensive to obtain for graphs. Aiming to bridge this gap, we characterize distribution shifts on graphs with causal models, and show that the OOD generalization on graphs with invariance principle is possible by identifying an invariant subgraph for making predictions. We propose a novel framework to explicitly model this process using a contrastive strategy. By contrasting the estimated invariant subgraphs, our framework can provably identify the underlying invariant subgraph under mild assumptions. Experiments across several synthetic and real-world datasets demonstrate the state-of-the-art OOD generalization ability of our method.