An Adaptive Incremental Gradient Method With Support for Non-Euclidean Norms
Paper and Code
Apr 28, 2022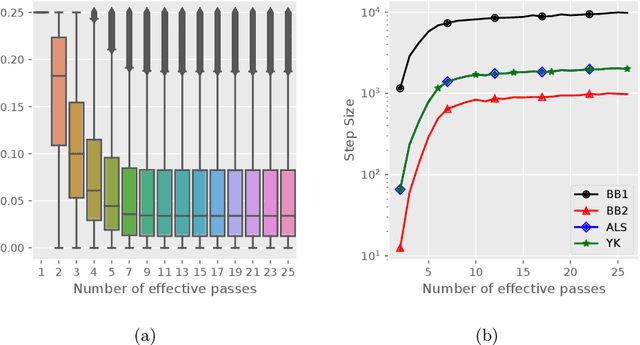
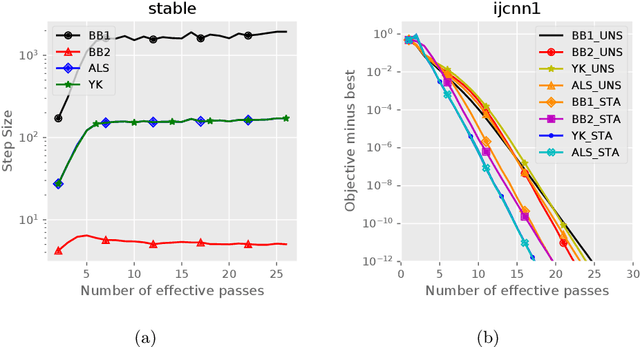
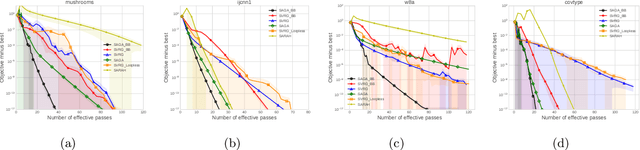
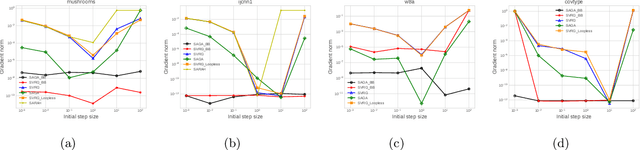
Stochastic variance reduced methods have shown strong performance in solving finite-sum problems. However, these methods usually require the users to manually tune the step-size, which is time-consuming or even infeasible for some large-scale optimization tasks. To overcome the problem, we propose and analyze several novel adaptive variants of the popular SAGA algorithm. Eventually, we design a variant of Barzilai-Borwein step-size which is tailored for the incremental gradient method to ensure memory efficiency and fast convergence. We establish its convergence guarantees under general settings that allow non-Euclidean norms in the definition of smoothness and the composite objectives, which cover a broad range of applications in machine learning. We improve the analysis of SAGA to support non-Euclidean norms, which fills the void of existing work. Numerical experiments on standard datasets demonstrate a competitive performance of the proposed algorithm compared with existing variance-reduced methods and their adaptive variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge