EndoVLA: Dual-Phase Vision-Language-Action Model for Autonomous Tracking in Endoscopy

In endoscopic procedures, autonomous tracking of abnormal regions and following circumferential cutting markers can significantly reduce the cognitive burden on endoscopists. However, conventional model-based pipelines are fragile for each component (e.g., detection, motion planning) requires manual tuning and struggles to incorporate high-level endoscopic intent, leading to poor generalization across diverse scenes. Vision-Language-Action (VLA) models, which integrate visual perception, language grounding, and motion planning within an end-to-end framework, offer a promising alternative by semantically adapting to surgeon prompts without manual recalibration. Despite their potential, applying VLA models to robotic endoscopy presents unique challenges due to the complex and dynamic anatomical environments of the gastrointestinal (GI) tract. To address this, we introduce EndoVLA, designed specifically for continuum robots in GI interventions. Given endoscopic images and surgeon-issued tracking prompts, EndoVLA performs three core tasks: (1) polyp tracking, (2) delineation and following of abnormal mucosal regions, and (3) adherence to circular markers during circumferential cutting. To tackle data scarcity and domain shifts, we propose a dual-phase strategy comprising supervised fine-tuning on our EndoVLA-Motion dataset and reinforcement fine-tuning with task-aware rewards. Our approach significantly improves tracking performance in endoscopy and enables zero-shot generalization in diverse scenes and complex sequential tasks.

Efficient Private SCO for Heavy-Tailed Data via Clipping

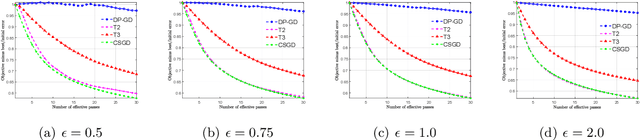
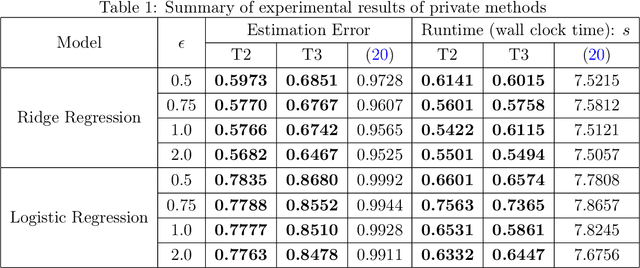
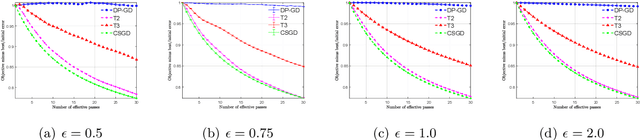
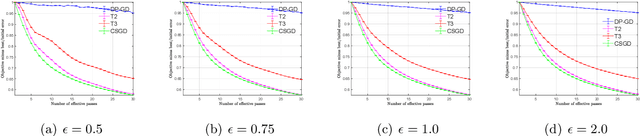
We consider stochastic convex optimization for heavy-tailed data with the guarantee of being differentially private (DP). Prior work on this problem is restricted to the gradient descent (GD) method, which is inefficient for large-scale problems. In this paper, we resolve this issue and derive the first high-probability bounds for private stochastic method with clipping. For general convex problems, we derive excess population risks $\Tilde{O}\left(\frac{d^{1/7}\sqrt{\ln\frac{(n \epsilon)^2}{\beta d}}}{(n\epsilon)^{2/7}}\right)$ and $\Tilde{O}\left(\frac{d^{1/7}\ln\frac{(n\epsilon)^2}{\beta d}}{(n\epsilon)^{2/7}}\right)$ under bounded or unbounded domain assumption, respectively (here $n$ is the sample size, $d$ is the dimension of the data, $\beta$ is the confidence level and $\epsilon$ is the private level). Then, we extend our analysis to the strongly convex case and non-smooth case (which works for generalized smooth objectives with H$\ddot{\text{o}}$lder-continuous gradients). We establish new excess risk bounds without bounded domain assumption. The results above achieve lower excess risks and gradient complexities than existing methods in their corresponding cases. Numerical experiments are conducted to justify the theoretical improvement.

An Adaptive Incremental Gradient Method With Support for Non-Euclidean Norms

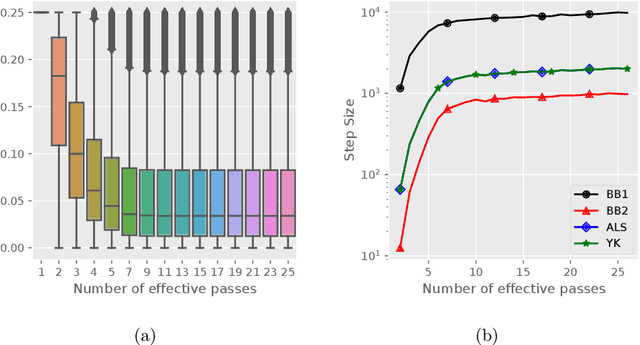
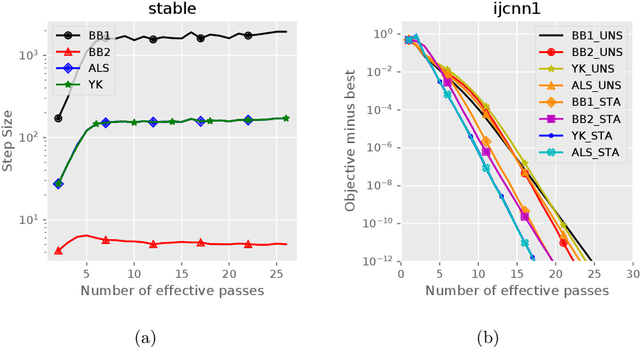
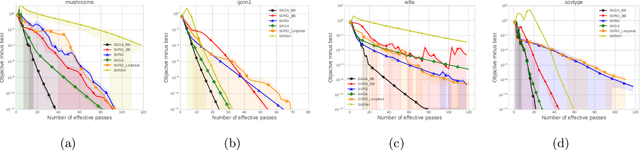
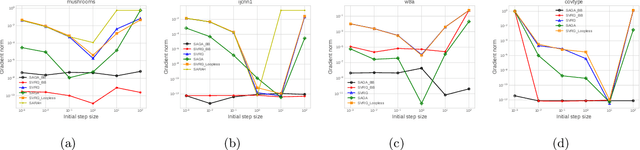
Stochastic variance reduced methods have shown strong performance in solving finite-sum problems. However, these methods usually require the users to manually tune the step-size, which is time-consuming or even infeasible for some large-scale optimization tasks. To overcome the problem, we propose and analyze several novel adaptive variants of the popular SAGA algorithm. Eventually, we design a variant of Barzilai-Borwein step-size which is tailored for the incremental gradient method to ensure memory efficiency and fast convergence. We establish its convergence guarantees under general settings that allow non-Euclidean norms in the definition of smoothness and the composite objectives, which cover a broad range of applications in machine learning. We improve the analysis of SAGA to support non-Euclidean norms, which fills the void of existing work. Numerical experiments on standard datasets demonstrate a competitive performance of the proposed algorithm compared with existing variance-reduced methods and their adaptive variants.