ControlNeXt: Powerful and Efficient Control for Image and Video Generation

Diffusion models have demonstrated remarkable and robust abilities in both image and video generation. To achieve greater control over generated results, researchers introduce additional architectures, such as ControlNet, Adapters and ReferenceNet, to integrate conditioning controls. However, current controllable generation methods often require substantial additional computational resources, especially for video generation, and face challenges in training or exhibit weak control. In this paper, we propose ControlNeXt: a powerful and efficient method for controllable image and video generation. We first design a more straightforward and efficient architecture, replacing heavy additional branches with minimal additional cost compared to the base model. Such a concise structure also allows our method to seamlessly integrate with other LoRA weights, enabling style alteration without the need for additional training. As for training, we reduce up to 90% of learnable parameters compared to the alternatives. Furthermore, we propose another method called Cross Normalization (CN) as a replacement for Zero-Convolution' to achieve fast and stable training convergence. We have conducted various experiments with different base models across images and videos, demonstrating the robustness of our method.

A Representation Learning Framework for Property Graphs

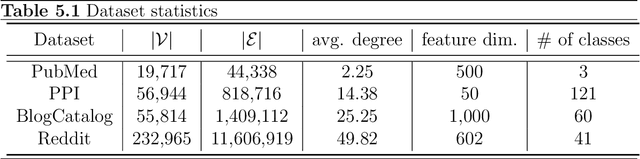
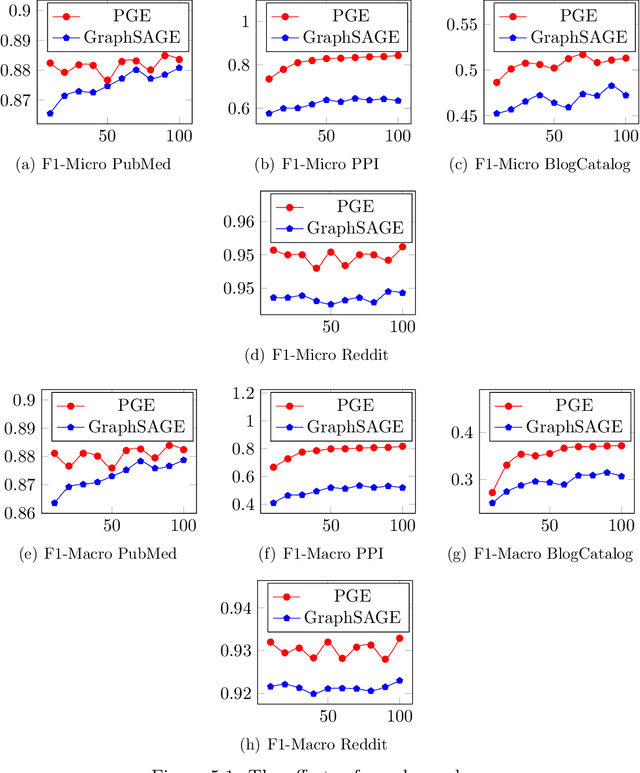
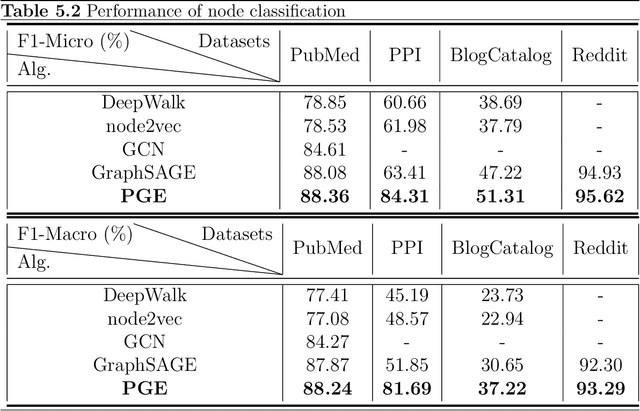
Representation learning on graphs, also called graph embedding, has demonstrated its significant impact on a series of machine learning applications such as classification, prediction and recommendation. However, existing work has largely ignored the rich information contained in the properties (or attributes) of both nodes and edges of graphs in modern applications, e.g., those represented by property graphs. To date, most existing graph embedding methods either focus on plain graphs with only the graph topology, or consider properties on nodes only. We propose PGE, a graph representation learning framework that incorporates both node and edge properties into the graph embedding procedure. PGE uses node clustering to assign biases to differentiate neighbors of a node and leverages multiple data-driven matrices to aggregate the property information of neighbors sampled based on a biased strategy. PGE adopts the popular inductive model for neighborhood aggregation. We provide detailed analyses on the efficacy of our method and validate the performance of PGE by showing how PGE achieves better embedding results than the state-of-the-art graph embedding methods on benchmark applications such as node classification and link prediction over real-world datasets.

Measuring and Improving the Use of Graph Information in Graph Neural Networks

Graph neural networks (GNNs) have been widely used for representation learning on graph data. However, there is limited understanding on how much performance GNNs actually gain from graph data. This paper introduces a context-surrounding GNN framework and proposes two smoothness metrics to measure the quantity and quality of information obtained from graph data. A new GNN model, called CS-GNN, is then designed to improve the use of graph information based on the smoothness values of a graph. CS-GNN is shown to achieve better performance than existing methods in different types of real graphs.

Efficient Private SCO for Heavy-Tailed Data via Clipping

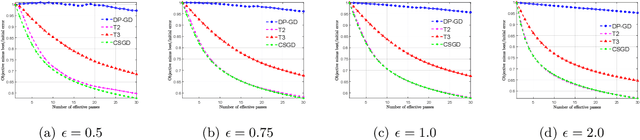
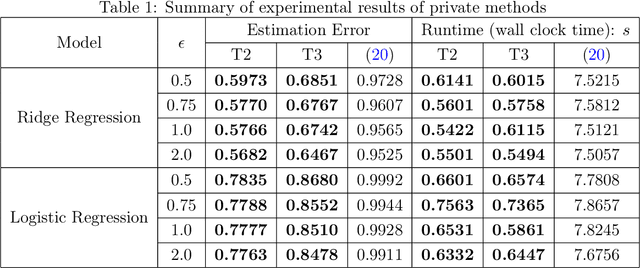
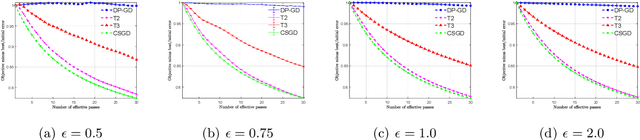
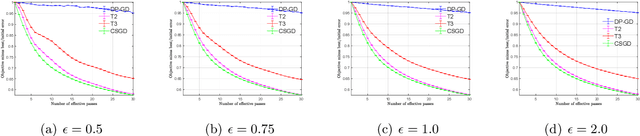
We consider stochastic convex optimization for heavy-tailed data with the guarantee of being differentially private (DP). Prior work on this problem is restricted to the gradient descent (GD) method, which is inefficient for large-scale problems. In this paper, we resolve this issue and derive the first high-probability bounds for private stochastic method with clipping. For general convex problems, we derive excess population risks $\Tilde{O}\left(\frac{d^{1/7}\sqrt{\ln\frac{(n \epsilon)^2}{\beta d}}}{(n\epsilon)^{2/7}}\right)$ and $\Tilde{O}\left(\frac{d^{1/7}\ln\frac{(n\epsilon)^2}{\beta d}}{(n\epsilon)^{2/7}}\right)$ under bounded or unbounded domain assumption, respectively (here $n$ is the sample size, $d$ is the dimension of the data, $\beta$ is the confidence level and $\epsilon$ is the private level). Then, we extend our analysis to the strongly convex case and non-smooth case (which works for generalized smooth objectives with H$\ddot{\text{o}}$lder-continuous gradients). We establish new excess risk bounds without bounded domain assumption. The results above achieve lower excess risks and gradient complexities than existing methods in their corresponding cases. Numerical experiments are conducted to justify the theoretical improvement.

Understanding and Improving Proximity Graph based Maximum Inner Product Search

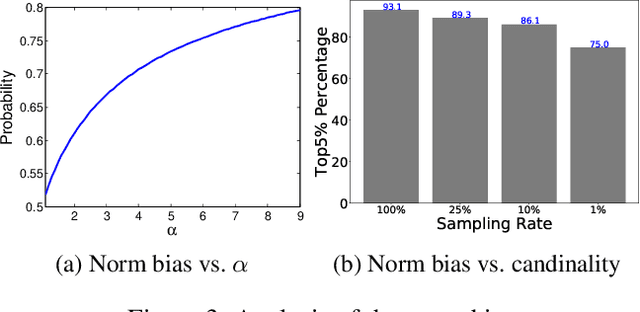
The inner-product navigable small world graph (ip-NSW) represents the state-of-the-art method for approximate maximum inner product search (MIPS) and it can achieve an order of magnitude speedup over the fastest baseline. However, to date it is still unclear where its exceptional performance comes from. In this paper, we show that there is a strong norm bias in the MIPS problem, which means that the large norm items are very likely to become the result of MIPS. Then we explain the good performance of ip-NSW as matching the norm bias of the MIPS problem - large norm items have big in-degrees in the ip-NSW proximity graph and a walk on the graph spends the majority of computation on these items, thus effectively avoids unnecessary computation on small norm items. Furthermore, we propose the ip-NSW+ algorithm, which improves ip-NSW by introducing an additional angular proximity graph. Search is first conducted on the angular graph to find the angular neighbors of a query and then the MIPS neighbors of these angular neighbors are used to initialize the candidate pool for search on the inner-product proximity graph. Experiment results show that ip-NSW+ consistently and significantly outperforms ip-NSW and provides more robust performance under different data distributions.