Efficient Private SCO for Heavy-Tailed Data via Clipping

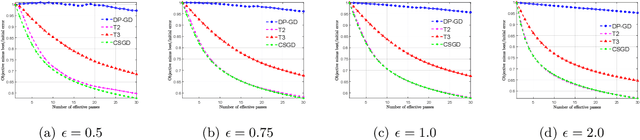
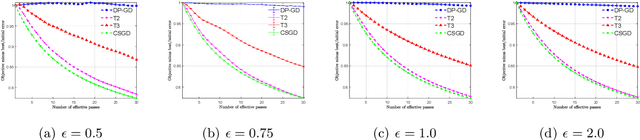
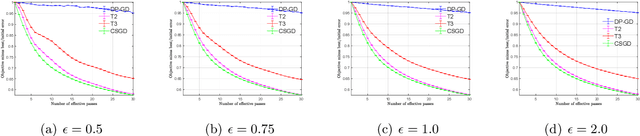
We consider stochastic convex optimization for heavy-tailed data with the guarantee of being differentially private (DP). Prior work on this problem is restricted to the gradient descent (GD) method, which is inefficient for large-scale problems. In this paper, we resolve this issue and derive the first high-probability bounds for private stochastic method with clipping. For general convex problems, we derive excess population risks $\Tilde{O}\left(\frac{d^{1/7}\sqrt{\ln\frac{(n \epsilon)^2}{\beta d}}}{(n\epsilon)^{2/7}}\right)$ and $\Tilde{O}\left(\frac{d^{1/7}\ln\frac{(n\epsilon)^2}{\beta d}}{(n\epsilon)^{2/7}}\right)$ under bounded or unbounded domain assumption, respectively (here $n$ is the sample size, $d$ is the dimension of the data, $\beta$ is the confidence level and $\epsilon$ is the private level). Then, we extend our analysis to the strongly convex case and non-smooth case (which works for generalized smooth objectives with H$\ddot{\text{o}}$lder-continuous gradients). We establish new excess risk bounds without bounded domain assumption. The results above achieve lower excess risks and gradient complexities than existing methods in their corresponding cases. Numerical experiments are conducted to justify the theoretical improvement.