Invariance Principle Meets Out-of-Distribution Generalization on Graphs

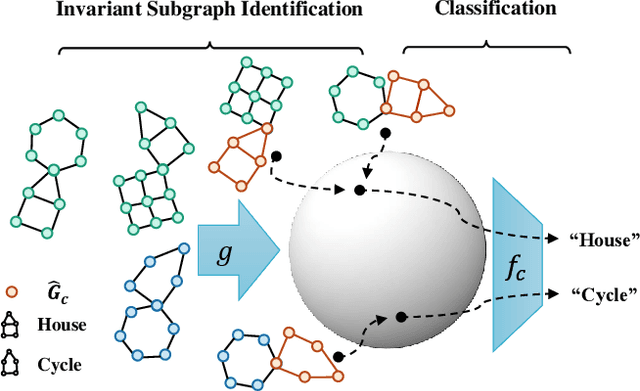
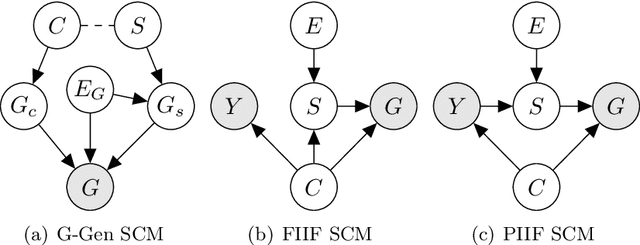
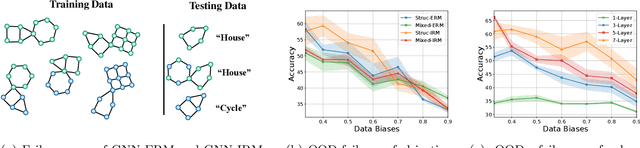
Despite recent developments in using the invariance principle from causality to enable out-of-distribution (OOD) generalization on Euclidean data, e.g., images, studies on graph data are limited. Different from images, the complex nature of graphs poses unique challenges that thwart the adoption of the invariance principle for OOD generalization. In particular, distribution shifts on graphs can happen at both structure-level and attribute-level, which increases the difficulty of capturing the invariance. Moreover, domain or environment partitions, which are often required by OOD methods developed on Euclidean data, can be expensive to obtain for graphs. Aiming to bridge this gap, we characterize distribution shifts on graphs with causal models, and show that the OOD generalization on graphs with invariance principle is possible by identifying an invariant subgraph for making predictions. We propose a novel framework to explicitly model this process using a contrastive strategy. By contrasting the estimated invariant subgraphs, our framework can provably identify the underlying invariant subgraph under mild assumptions. Experiments across several synthetic and real-world datasets demonstrate the state-of-the-art OOD generalization ability of our method.