Rethinking Graph Regularization For Graph Neural Networks
Paper and Code
Sep 04, 2020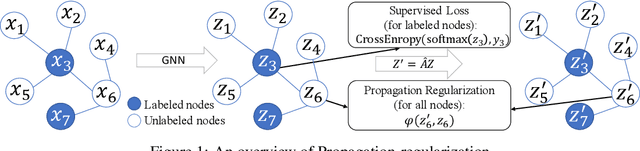
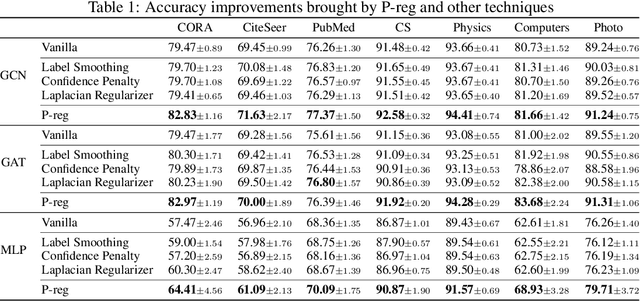
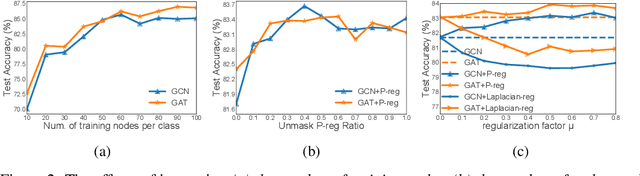
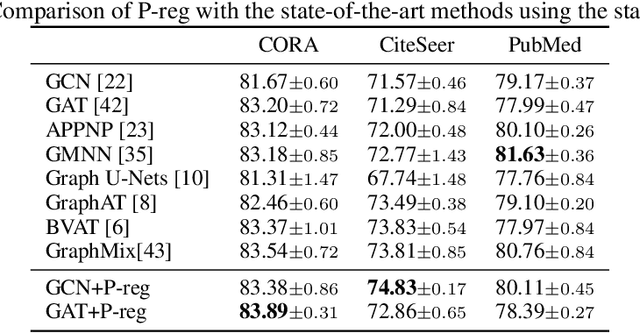
The graph Laplacian regularization term is usually used in semi-supervised node classification to provide graph structure information for a model $f(X)$. However, with the recent popularity of graph neural networks (GNNs), directly encoding graph structure $A$ into a model, i.e., $f(A, X)$, has become the more common approach. While we show that graph Laplacian regularization $f(X)^\top \Delta f(X)$ brings little-to-no benefit to existing GNNs, we propose a simple but non-trivial variant of graph Laplacian regularization, called Propagation-regularization (P-reg), to boost the performance of existing GNN models. We provide formal analyses to show that P-reg not only infuses extra information (that is not captured by the traditional graph Laplacian regularization) into GNNs, but also has the capacity equivalent to an infinite-depth graph convolutional network. The code is available at https://github.com/yang-han/P-reg.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge