Improving Graph Representation Learning by Contrastive Regularization

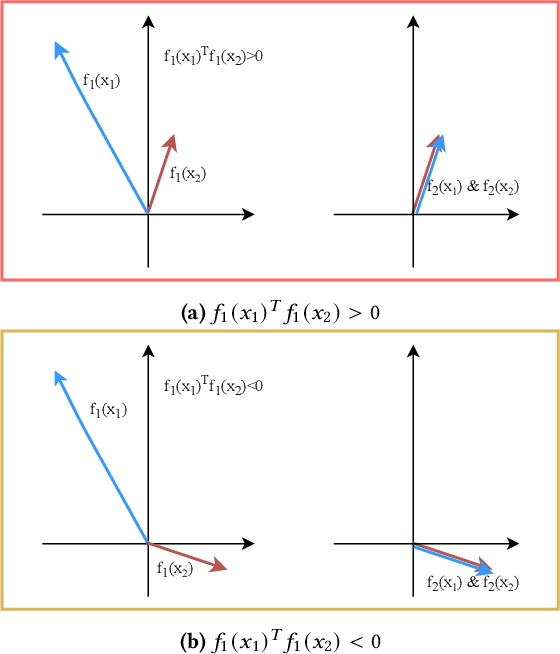
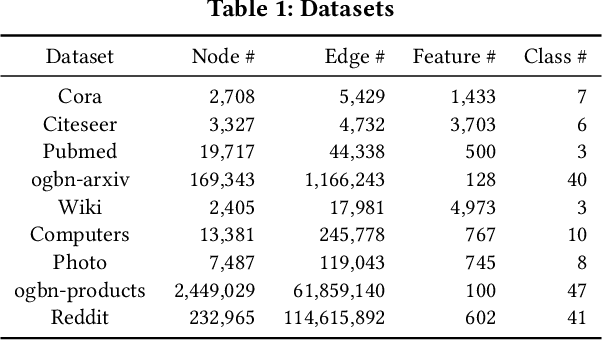
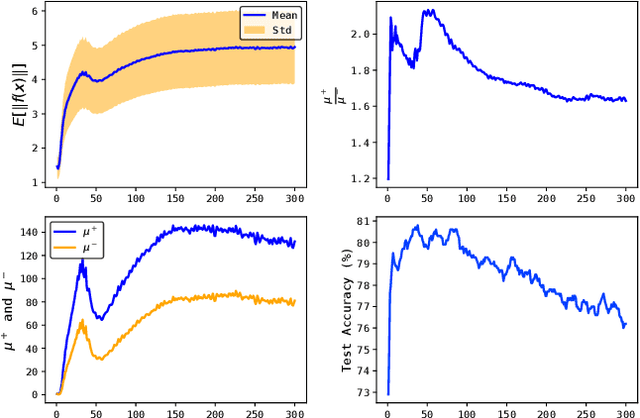
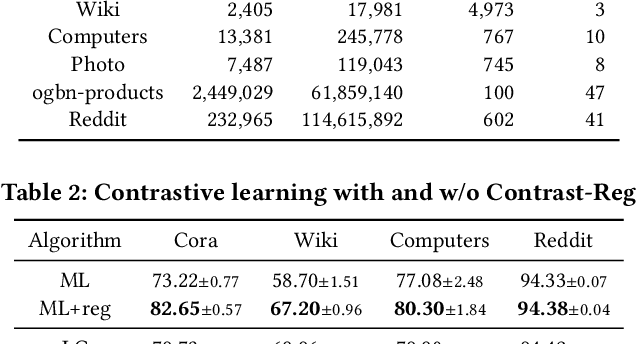
Graph representation learning is an important task with applications in various areas such as online social networks, e-commerce networks, WWW, and semantic webs. For unsupervised graph representation learning, many algorithms such as Node2Vec and Graph-SAGE make use of "negative sampling" and/or noise contrastive estimation loss. This bears similar ideas to contrastive learning, which "contrasts" the node representation similarities of semantically similar (positive) pairs against those of negative pairs. However, despite the success of contrastive learning, we found that directly applying this technique to graph representation learning models (e.g., graph convolutional networks) does not always work. We theoretically analyze the generalization performance and propose a light-weight regularization term that avoids the high scales of node representations' norms and the high variance among them to improve the generalization performance. Our experimental results further validate that this regularization term significantly improves the representation quality across different node similarity definitions and outperforms the state-of-the-art methods.

Understanding Graph Neural Networks from Graph Signal Denoising Perspectives

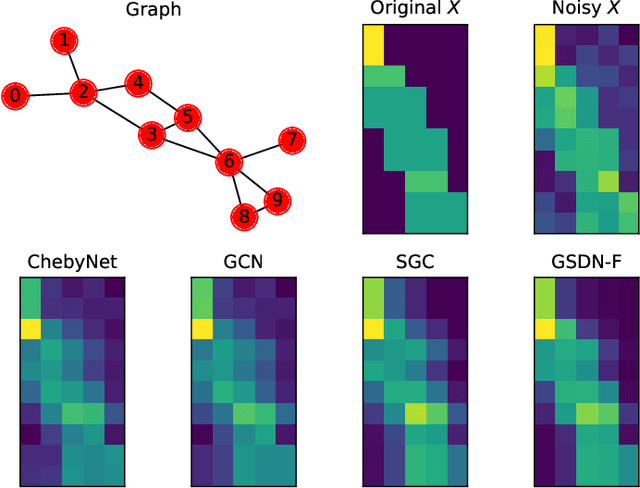
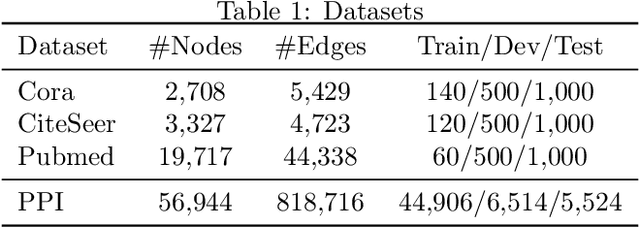
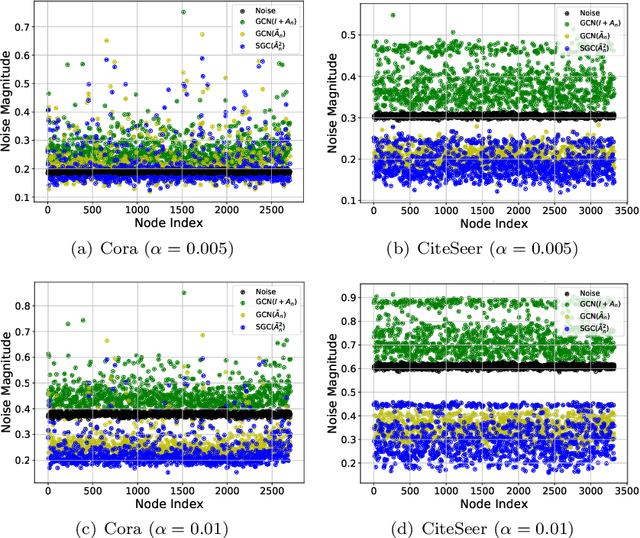
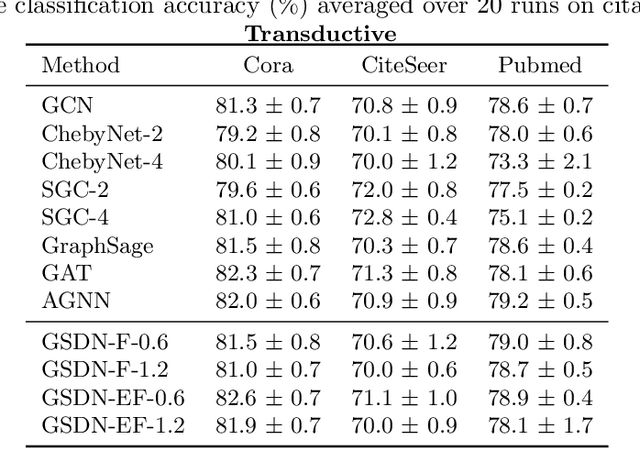
Graph neural networks (GNNs) have attracted much attention because of their excellent performance on tasks such as node classification. However, there is inadequate understanding on how and why GNNs work, especially for node representation learning. This paper aims to provide a theoretical framework to understand GNNs, specifically, spectral graph convolutional networks and graph attention networks, from graph signal denoising perspectives. Our framework shows that GNNs are implicitly solving graph signal denoising problems: spectral graph convolutions work as denoising node features, while graph attentions work as denoising edge weights. We also show that a linear self-attention mechanism is able to compete with the state-of-the-art graph attention methods. Our theoretical results further lead to two new models, GSDN-F and GSDN-EF, which work effectively for graphs with noisy node features and/or noisy edges. We validate our theoretical findings and also the effectiveness of our new models by experiments on benchmark datasets. The source code is available at \url{https://github.com/fuguoji/GSDN}.