C-kNN-LSH: A Nearest-Neighbor Algorithm for Sequential Counterfactual Inference

Estimating causal effects from longitudinal trajectories is central to understanding the progression of complex conditions and optimizing clinical decision-making, such as comorbidities and long COVID recovery. We introduce \emph{C-kNN--LSH}, a nearest-neighbor framework for sequential causal inference designed to handle such high-dimensional, confounded situations. By utilizing locality-sensitive hashing, we efficiently identify ``clinical twins'' with similar covariate histories, enabling local estimation of conditional treatment effects across evolving disease states. To mitigate bias from irregular sampling and shifting patient recovery profiles, we integrate neighborhood estimator with a doubly-robust correction. Theoretical analysis guarantees our estimator is consistent and second-order robust to nuisance error. Evaluated on a real-world Long COVID cohort with 13,511 participants, \emph{C-kNN-LSH} demonstrates superior performance in capturing recovery heterogeneity and estimating policy values compared to existing baselines.

Optimal Budgeted Adaptation of Large Language Models

The trade-off between labeled data availability and downstream accuracy remains a central challenge in fine-tuning large language models (LLMs). We propose a principled framework for \emph{budget-aware supervised fine-tuning} by casting LLM adaptation as a contextual Stackelberg game. In our formulation, the learner (leader) commits to a scoring policy and a label-querying strategy, while an adaptive environment (follower) selects challenging supervised alternatives in response. To explicitly address label efficiency, we incorporate a finite supervision budget directly into the learning objective. Our algorithm operates in the full-feedback regime and achieves $\tilde{O}(d\sqrt{T})$ regret under standard linear contextual assumptions. We extend the framework with a Largest-Latency-First (LLF) confidence gate that selectively queries labels, achieving a budget-aware regret bound of $\tilde{O}(\sqrt{dB} + c\sqrt{B})$ with $B=βT$.

Metric-Fair Prompting: Treating Similar Samples Similarly

We introduce \emph{Metric-Fair Prompting}, a fairness-aware prompting framework that guides large language models (LLMs) to make decisions under metric-fairness constraints. In the application of multiple-choice medical question answering, each {(question, option)} pair is treated as a binary instance with label $+1$ (correct) or $-1$ (incorrect). To promote {individual fairness}~--~treating similar instances similarly~--~we compute question similarity using NLP embeddings and solve items in \emph{joint pairs of similar questions} rather than in isolation. The prompt enforces a global decision protocol: extract decisive clinical features, map each \((\text{question}, \text{option})\) to a score $f(x)$ that acts as confidence, and impose a Lipschitz-style constraint so that similar inputs receive similar scores and, hence, consistent outputs. Evaluated on the {MedQA (US)} benchmark, Metric-Fair Prompting is shown to improve performance over standard single-item prompting, demonstrating that fairness-guided, confidence-oriented reasoning can enhance LLM accuracy on high-stakes clinical multiple-choice questions.

Attribute-Efficient PAC Learning of Sparse Halfspaces with Constant Malicious Noise Rate

Attribute-efficient learning of sparse halfspaces has been a fundamental problem in machine learning theory. In recent years, machine learning algorithms are faced with prevalent data corruptions or even adversarial attacks. It is of central interest to design efficient algorithms that are robust to noise corruptions. In this paper, we consider that there exists a constant amount of malicious noise in the data and the goal is to learn an underlying $s$-sparse halfspace $w^* \in \mathbb{R}^d$ with $\text{poly}(s,\log d)$ samples. Specifically, we follow a recent line of works and assume that the underlying distribution satisfies a certain concentration condition and a margin condition at the same time. Under such conditions, we show that attribute-efficiency can be achieved by simple variants to existing hinge loss minimization programs. Our key contribution includes: 1) an attribute-efficient PAC learning algorithm that works under constant malicious noise rate; 2) a new gradient analysis that carefully handles the sparsity constraint in hinge loss minimization.

MIMIC-\RNum{4}-Ext-22MCTS: A 22 Millions-Event Temporal Clinical Time-Series Dataset with Relative Timestamp for Risk Prediction

Clinical risk prediction based on machine learning algorithms plays a vital role in modern healthcare. A crucial component in developing a reliable prediction model is collecting high-quality time series clinical events. In this work, we release such a dataset that consists of 22,588,586 Clinical Time Series events, which we term MIMIC-\RNum{4}-Ext-22MCTS. Our source data are discharge summaries selected from the well-known yet unstructured MIMIC-IV-Note \cite{Johnson2023-pg}. We then extract clinical events as short text span from the discharge summaries, along with the timestamps of these events as temporal information. The general-purpose MIMIC-IV-Note pose specific challenges for our work: it turns out that the discharge summaries are too lengthy for typical natural language models to process, and the clinical events of interest often are not accompanied with explicit timestamps. Therefore, we propose a new framework that works as follows: 1) we break each discharge summary into manageably small text chunks; 2) we apply contextual BM25 and contextual semantic search to retrieve chunks that have a high potential of containing clinical events; and 3) we carefully design prompts to teach the recently released Llama-3.1-8B \cite{touvron2023llama} model to identify or infer temporal information of the chunks. We show that the obtained dataset is so informative and transparent that standard models fine-tuned on our dataset are achieving significant improvements in healthcare applications. In particular, the BERT model fine-tuned based on our dataset achieves 10\% improvement in accuracy on medical question answering task, and 3\% improvement in clinical trial matching task compared with the classic BERT. The GPT-2 model, fine-tuned on our dataset, produces more clinically reliable results for clinical questions.

Towards Efficient Contrastive PAC Learning

We study contrastive learning under the PAC learning framework. While a series of recent works have shown statistical results for learning under contrastive loss, based either on the VC-dimension or Rademacher complexity, their algorithms are inherently inefficient or not implying PAC guarantees. In this paper, we consider contrastive learning of the fundamental concept of linear representations. Surprisingly, even under such basic setting, the existence of efficient PAC learners is largely open. We first show that the problem of contrastive PAC learning of linear representations is intractable to solve in general. We then show that it can be relaxed to a semi-definite program when the distance between contrastive samples is measured by the $\ell_2$-norm. We then establish generalization guarantees based on Rademacher complexity, and connect it to PAC guarantees under certain contrastive large-margin conditions. To the best of our knowledge, this is the first efficient PAC learning algorithm for contrastive learning.

Efficient PAC Learning of Halfspaces with Constant Malicious Noise Rate

Understanding noise tolerance of learning algorithms under certain conditions is a central quest in learning theory. In this work, we study the problem of computationally efficient PAC learning of halfspaces in the presence of malicious noise, where an adversary can corrupt both instances and labels of training samples. The best-known noise tolerance either depends on a target error rate under distributional assumptions or on a margin parameter under large-margin conditions. In this work, we show that when both types of conditions are satisfied, it is possible to achieve {\em constant} noise tolerance by minimizing a reweighted hinge loss. Our key ingredients include: 1) an efficient algorithm that finds weights to control the gradient deterioration from corrupted samples, and 2) a new analysis on the robustness of the hinge loss equipped with such weights.

FedLED: Label-Free Equipment Fault Diagnosis with Vertical Federated Transfer Learning

Intelligent equipment fault diagnosis based on Federated Transfer Learning (FTL) attracts considerable attention from both academia and industry. It allows real-world industrial agents with limited samples to construct a fault diagnosis model without jeopardizing their raw data privacy. Existing approaches, however, can neither address the intense sample heterogeneity caused by different working conditions of practical agents, nor the extreme fault label scarcity, even zero, of newly deployed equipment. To address these issues, we present FedLED, the first unsupervised vertical FTL equipment fault diagnosis method, where knowledge of the unlabeled target domain is further exploited for effective unsupervised model transfer. Results of extensive experiments using data of real equipment monitoring demonstrate that FedLED obviously outperforms SOTA approaches in terms of both diagnosis accuracy (up to 4.13 times) and generality. We expect our work to inspire further study on label-free equipment fault diagnosis systematically enhanced by target domain knowledge.

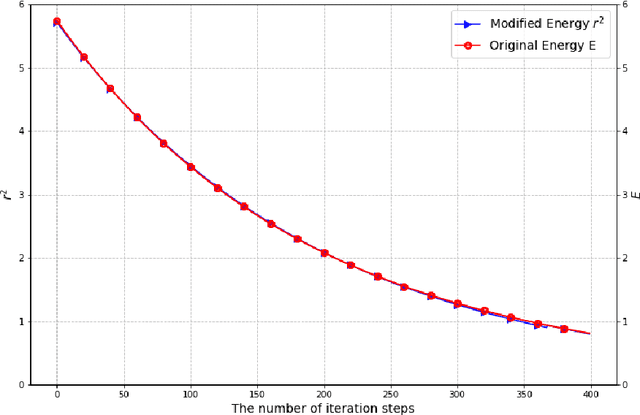
An Element-wise RSAV Algorithm for Unconstrained Optimization Problems

We present a novel optimization algorithm, element-wise relaxed scalar auxiliary variable (E-RSAV), that satisfies an unconditional energy dissipation law and exhibits improved alignment between the modified and the original energy. Our algorithm features rigorous proofs of linear convergence in the convex setting. Furthermore, we present a simple accelerated algorithm that improves the linear convergence rate to super-linear in the univariate case. We also propose an adaptive version of E-RSAV with Steffensen step size. We validate the robustness and fast convergence of our algorithm through ample numerical experiments.

Energy-Dissipative Evolutionary Deep Operator Neural Networks

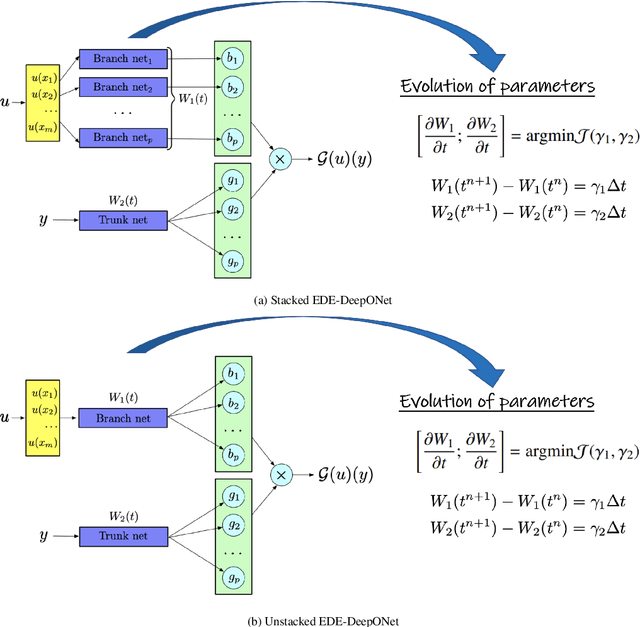
Energy-Dissipative Evolutionary Deep Operator Neural Network is an operator learning neural network. It is designed to seed numerical solutions for a class of partial differential equations instead of a single partial differential equation, such as partial differential equations with different parameters or different initial conditions. The network consists of two sub-networks, the Branch net and the Trunk net. For an objective operator G, the Branch net encodes different input functions u at the same number of sensors, and the Trunk net evaluates the output function at any location. By minimizing the error between the evaluated output q and the expected output G(u)(y), DeepONet generates a good approximation of the operator G. In order to preserve essential physical properties of PDEs, such as the Energy Dissipation Law, we adopt a scalar auxiliary variable approach to generate the minimization problem. It introduces a modified energy and enables unconditional energy dissipation law at the discrete level. By taking the parameter as a function of time t, this network can predict the accurate solution at any further time with feeding data only at the initial state. The data needed can be generated by the initial conditions, which are readily available. In order to validate the accuracy and efficiency of our neural networks, we provide numerical simulations of several partial differential equations, including heat equations, parametric heat equations and Allen-Cahn equations.