Learning Large Scale Sparse Models
Paper and Code
Jan 26, 2023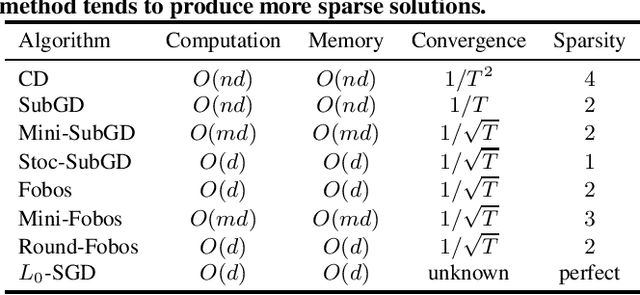
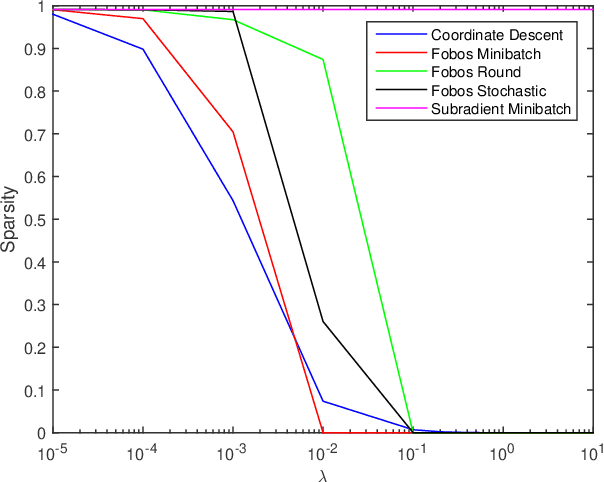
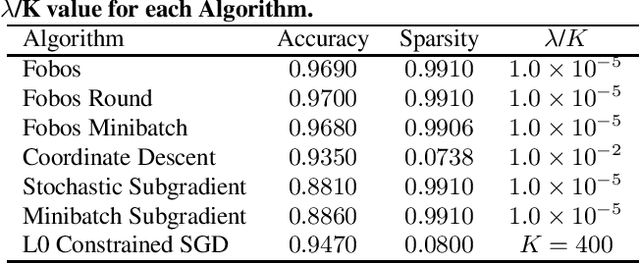
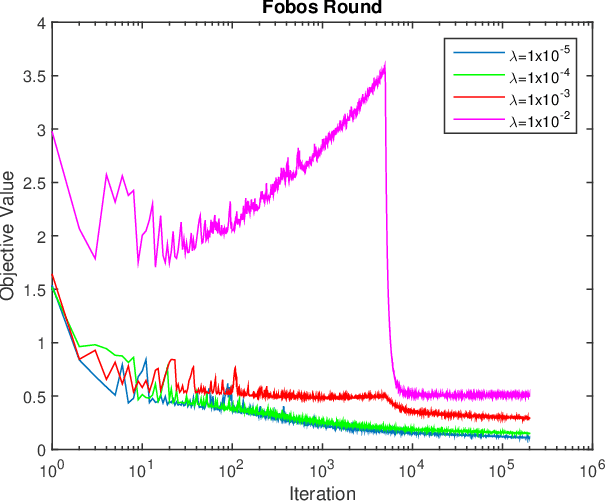
In this work, we consider learning sparse models in large scale settings, where the number of samples and the feature dimension can grow as large as millions or billions. Two immediate issues occur under such challenging scenario: (i) computational cost; (ii) memory overhead. In particular, the memory issue precludes a large volume of prior algorithms that are based on batch optimization technique. To remedy the problem, we propose to learn sparse models such as Lasso in an online manner where in each iteration, only one randomly chosen sample is revealed to update a sparse iterate. Thereby, the memory cost is independent of the sample size and gradient evaluation for one sample is efficient. Perhaps amazingly, we find that with the same parameter, sparsity promoted by batch methods is not preserved in online fashion. We analyze such interesting phenomenon and illustrate some effective variants including mini-batch methods and a hard thresholding based stochastic gradient algorithm. Extensive experiments are carried out on a public dataset which supports our findings and algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge