Energy-Dissipative Evolutionary Deep Operator Neural Networks
Paper and Code
Jun 09, 2023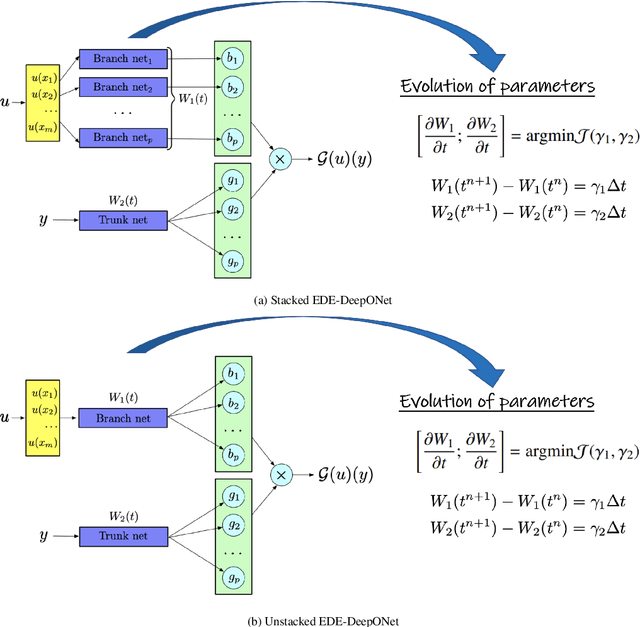

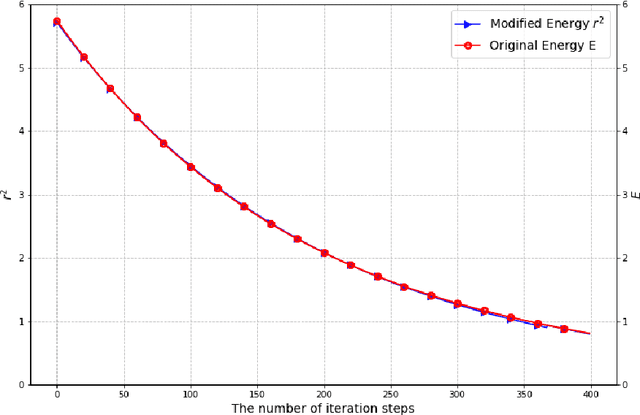

Energy-Dissipative Evolutionary Deep Operator Neural Network is an operator learning neural network. It is designed to seed numerical solutions for a class of partial differential equations instead of a single partial differential equation, such as partial differential equations with different parameters or different initial conditions. The network consists of two sub-networks, the Branch net and the Trunk net. For an objective operator G, the Branch net encodes different input functions u at the same number of sensors, and the Trunk net evaluates the output function at any location. By minimizing the error between the evaluated output q and the expected output G(u)(y), DeepONet generates a good approximation of the operator G. In order to preserve essential physical properties of PDEs, such as the Energy Dissipation Law, we adopt a scalar auxiliary variable approach to generate the minimization problem. It introduces a modified energy and enables unconditional energy dissipation law at the discrete level. By taking the parameter as a function of time t, this network can predict the accurate solution at any further time with feeding data only at the initial state. The data needed can be generated by the initial conditions, which are readily available. In order to validate the accuracy and efficiency of our neural networks, we provide numerical simulations of several partial differential equations, including heat equations, parametric heat equations and Allen-Cahn equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge