Spectral-Temporal Fusion Representation for Person-in-Bed Detection

This study is based on the ICASSP 2025 Signal Processing Grand Challenge's Accelerometer-Based Person-in-Bed Detection Challenge, which aims to determine bed occupancy using accelerometer signals. The task is divided into two tracks: "in bed" and "not in bed" segmented detection, and streaming detection, facing challenges such as individual differences, posture variations, and external disturbances. We propose a spectral-temporal fusion-based feature representation method with mixup data augmentation, and adopt Intersection over Union (IoU) loss to optimize detection accuracy. In the two tracks, our method achieved outstanding results of 100.00% and 95.55% in detection scores, securing first place and third place, respectively.

Independent Feature Enhanced Crossmodal Fusion for Match-Mismatch Classification of Speech Stimulus and EEG Response

It is crucial for auditory attention decoding to classify matched and mismatched speech stimuli with corresponding EEG responses by exploring their relationship. However, existing methods often adopt two independent networks to encode speech stimulus and EEG response, which neglect the relationship between these signals from the two modalities. In this paper, we propose an independent feature enhanced crossmodal fusion model (IFE-CF) for match-mismatch classification, which leverages the fusion feature of the speech stimulus and the EEG response to achieve auditory EEG decoding. Specifically, our IFE-CF contains a crossmodal encoder to encode the speech stimulus and the EEG response with a two-branch structure connected via crossmodal attention mechanism in the encoding process, a multi-channel fusion module to fuse features of two modalities by aggregating the interaction feature obtained from the crossmodal encoder and the independent feature obtained from the speech stimulus and EEG response, and a predictor to give the matching result. In addition, the causal mask is introduced to consider the time delay of the speech-EEG pair in the crossmodal encoder, which further enhances the feature representation for match-mismatch classification. Experiments demonstrate our method's effectiveness with better classification accuracy, as compared with the baseline of the Auditory EEG Decoding Challenge 2023.

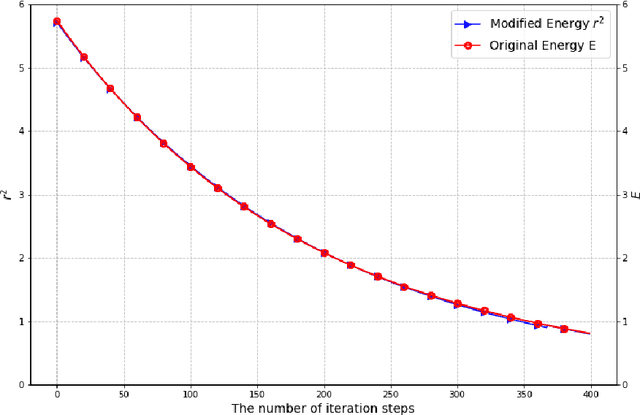
An Element-wise RSAV Algorithm for Unconstrained Optimization Problems

We present a novel optimization algorithm, element-wise relaxed scalar auxiliary variable (E-RSAV), that satisfies an unconditional energy dissipation law and exhibits improved alignment between the modified and the original energy. Our algorithm features rigorous proofs of linear convergence in the convex setting. Furthermore, we present a simple accelerated algorithm that improves the linear convergence rate to super-linear in the univariate case. We also propose an adaptive version of E-RSAV with Steffensen step size. We validate the robustness and fast convergence of our algorithm through ample numerical experiments.

Energy-Dissipative Evolutionary Deep Operator Neural Networks

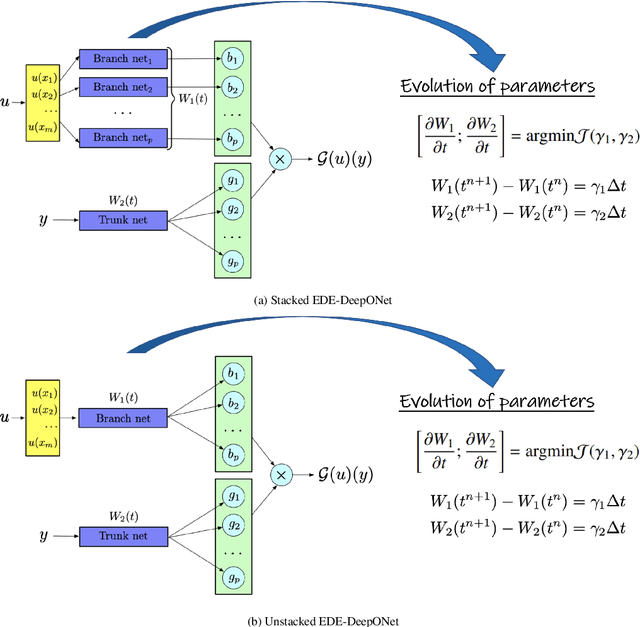
Energy-Dissipative Evolutionary Deep Operator Neural Network is an operator learning neural network. It is designed to seed numerical solutions for a class of partial differential equations instead of a single partial differential equation, such as partial differential equations with different parameters or different initial conditions. The network consists of two sub-networks, the Branch net and the Trunk net. For an objective operator G, the Branch net encodes different input functions u at the same number of sensors, and the Trunk net evaluates the output function at any location. By minimizing the error between the evaluated output q and the expected output G(u)(y), DeepONet generates a good approximation of the operator G. In order to preserve essential physical properties of PDEs, such as the Energy Dissipation Law, we adopt a scalar auxiliary variable approach to generate the minimization problem. It introduces a modified energy and enables unconditional energy dissipation law at the discrete level. By taking the parameter as a function of time t, this network can predict the accurate solution at any further time with feeding data only at the initial state. The data needed can be generated by the initial conditions, which are readily available. In order to validate the accuracy and efficiency of our neural networks, we provide numerical simulations of several partial differential equations, including heat equations, parametric heat equations and Allen-Cahn equations.