Bias Fitting to Mitigate Length Bias of Reward Model in RLHF

Reinforcement Learning from Human Feedback relies on reward models to align large language models with human preferences. However, RLHF often suffers from reward hacking, wherein policy learning exploits flaws in the trained reward model to maximize reward scores without genuinely aligning with human preferences. A significant example of such reward hacking is length bias, where reward models usually favor longer responses irrespective of actual response quality. Previous works on length bias have notable limitations, these approaches either mitigate bias without characterizing the bias form, or simply assume a linear length-reward relation. To accurately model the intricate nature of length bias and facilitate more effective bias mitigation, we propose FiMi-RM (Bias Fitting to Mitigate Length Bias of Reward Model in RLHF), a framework that autonomously learns and corrects underlying bias patterns. Our approach consists of three stages: First, we train a standard reward model which inherently contains length bias. Next, we deploy a lightweight fitting model to explicitly capture the non-linear relation between length and reward. Finally, we incorporate this learned relation into the reward model to debias. Experimental results demonstrate that FiMi-RM achieves a more balanced length-reward distribution. Furthermore, when applied to alignment algorithms, our debiased reward model improves length-controlled win rate and reduces verbosity without compromising its performance.

Multi-Level Aware Preference Learning: Enhancing RLHF for Complex Multi-Instruction Tasks

RLHF has emerged as a predominant approach for aligning artificial intelligence systems with human preferences, demonstrating exceptional and measurable efficacy in instruction following tasks; however, it exhibits insufficient compliance capabilities when confronted with complex multi-instruction tasks. Conventional approaches rely heavily on human annotation or more sophisticated large language models, thereby introducing substantial resource expenditure or potential bias concerns. Meanwhile, alternative synthetic methods that augment standard preference datasets often compromise the model's semantic quality. Our research identifies a critical oversight in existing techniques, which predominantly focus on comparing responses while neglecting valuable latent signals embedded within prompt inputs, and which only focus on preference disparities at the intra-sample level, while neglecting to account for the inter-sample level preference differentials that exist among preference data. To leverage these previously neglected indicators, we propose a novel Multi-level Aware Preference Learning (MAPL) framework, capable of enhancing multi-instruction capabilities. Specifically, for any given response in original preference data pairs, we construct varied prompts with a preference relation under different conditions, in order to learn intra-sample level preference disparities. Furthermore, for any given original preference pair, we synthesize multi-instruction preference pairs to capture preference discrepancies at the inter-sample level. Building on the two datasets constructed above, we consequently devise two sophisticated training objective functions. Subsequently, our framework integrates seamlessly into both Reward Modeling and Direct Preference Optimization paradigms. Through rigorous evaluation across multiple benchmarks, we empirically validate the efficacy of our framework.

Mitigating Hallucination in VideoLLMs via Temporal-Aware Activation Engineering

Multimodal large language models (MLLMs) have achieved remarkable progress in video understanding.However, hallucination, where the model generates plausible yet incorrect outputs, persists as a significant and under-addressed challenge in the video domain. Among existing solutions, activation engineering has proven successful in mitigating hallucinations in LLMs and ImageLLMs, yet its applicability to VideoLLMs remains largely unexplored. In this work, we are the first to systematically investigate the effectiveness and underlying mechanisms of activation engineering for mitigating hallucinations in VideoLLMs. We initially conduct an investigation of the key factors affecting the performance of activation engineering and find that a model's sensitivity to hallucination depends on $\textbf{temporal variation}$ rather than task type. Moreover, selecting appropriate internal modules and dataset for activation engineering is critical for reducing hallucination. Guided by these findings, we propose a temporal-aware activation engineering framework for VideoLLMs, which adaptively identifies and manipulates hallucination-sensitive modules based on the temporal variation characteristic, substantially mitigating hallucinations without additional LLM fine-tuning. Experiments across multiple models and benchmarks demonstrate that our method markedly reduces hallucination in VideoLLMs, thereby validating the robustness of our findings.

Disentangling Length Bias In Preference Learning Via Response-Conditioned Modeling

Reinforcement Learning from Human Feedback (RLHF) has achieved considerable success in aligning large language models (LLMs) by modeling human preferences with a learnable reward model and employing a reinforcement learning algorithm to maximize the reward model's scores. However, these reward models are susceptible to exploitation through various superficial confounding factors, with length bias emerging as a particularly significant concern. Moreover, while the pronounced impact of length bias on preference modeling suggests that LLMs possess an inherent sensitivity to length perception, our preliminary investigations reveal that fine-tuned LLMs consistently struggle to adhere to explicit length instructions. To address these two limitations, we propose a novel framework wherein the reward model explicitly differentiates between human semantic preferences and response length requirements. Specifically, we introduce a Response-conditioned Bradley-Terry (Rc-BT) model that enhances the reward model's capability in length bias mitigating and length instruction following, through training on our augmented dataset. Furthermore, we propose the Rc-DPO algorithm to leverage the Rc-BT model for direct policy optimization (DPO) of LLMs, simultaneously mitigating length bias and promoting adherence to length instructions. Extensive evaluations demonstrate that our approach substantially improves both preference modeling and length instruction compliance, with its effectiveness validated across various foundational models and preference datasets.

Heterogeneous Network Based Contrastive Learning Method for PolSAR Land Cover Classification

Polarimetric synthetic aperture radar (PolSAR) image interpretation is widely used in various fields. Recently, deep learning has made significant progress in PolSAR image classification. Supervised learning (SL) requires a large amount of labeled PolSAR data with high quality to achieve better performance, however, manually labeled data is insufficient. This causes the SL to fail into overfitting and degrades its generalization performance. Furthermore, the scattering confusion problem is also a significant challenge that attracts more attention. To solve these problems, this article proposes a Heterogeneous Network based Contrastive Learning method(HCLNet). It aims to learn high-level representation from unlabeled PolSAR data for few-shot classification according to multi-features and superpixels. Beyond the conventional CL, HCLNet introduces the heterogeneous architecture for the first time to utilize heterogeneous PolSAR features better. And it develops two easy-to-use plugins to narrow the domain gap between optics and PolSAR, including feature filter and superpixel-based instance discrimination, which the former is used to enhance the complementarity of multi-features, and the latter is used to increase the diversity of negative samples. Experiments demonstrate the superiority of HCLNet on three widely used PolSAR benchmark datasets compared with state-of-the-art methods. Ablation studies also verify the importance of each component. Besides, this work has implications for how to efficiently utilize the multi-features of PolSAR data to learn better high-level representation in CL and how to construct networks suitable for PolSAR data better.

Flowmind2Digital: The First Comprehensive Flowmind Recognition and Conversion Approach

Flowcharts and mind maps, collectively known as flowmind, are vital in daily activities, with hand-drawn versions facilitating real-time collaboration. However, there's a growing need to digitize them for efficient processing. Automated conversion methods are essential to overcome manual conversion challenges. Existing sketch recognition methods face limitations in practical situations, being field-specific and lacking digital conversion steps. Our paper introduces the Flowmind2digital method and hdFlowmind dataset to address these challenges. Flowmind2digital, utilizing neural networks and keypoint detection, achieves a record 87.3% accuracy on our dataset, surpassing previous methods by 11.9%. The hdFlowmind dataset, comprising 1,776 annotated flowminds across 22 scenarios, outperforms existing datasets. Additionally, our experiments emphasize the importance of simple graphics, enhancing accuracy by 9.3%.

A stochastic alternating minimizing method for sparse phase retrieval

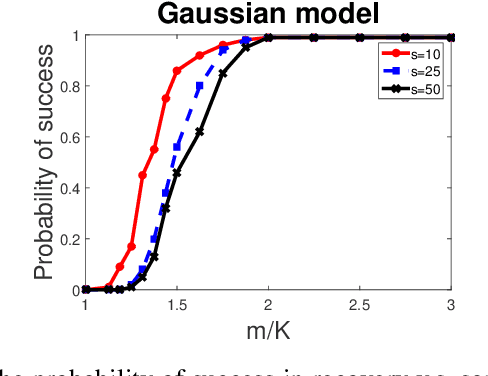
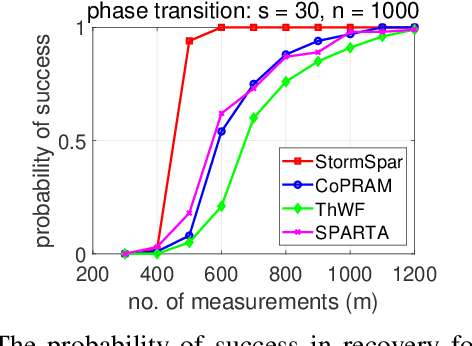
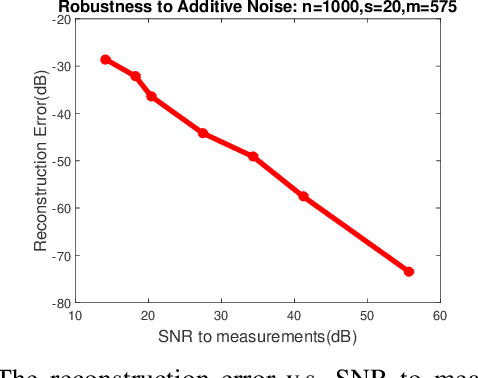
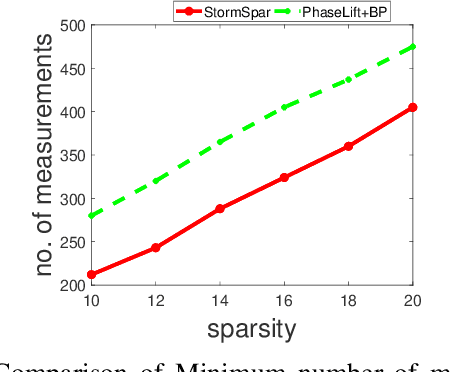
Sparse phase retrieval plays an important role in many fields of applied science and thus attracts lots of attention. In this paper, we propose a \underline{sto}chastic alte\underline{r}nating \underline{m}inimizing method for \underline{sp}arse ph\underline{a}se \underline{r}etrieval (\textit{StormSpar}) algorithm which {emprically} is able to recover $n$-dimensional $s$-sparse signals from only $O(s\,\mathrm{log}\, n)$ number of measurements without a desired initial value required by many existing methods. In \textit{StormSpar}, the hard-thresholding pursuit (HTP) algorithm is employed to solve the sparse constraint least square sub-problems. The main competitive feature of \textit{StormSpar} is that it converges globally requiring optimal order of number of samples with random initialization. Extensive numerical experiments are given to validate the proposed algorithm.

Sparse Recovery from Nonlinear Measurements with Applications in Bad Data Detection for Power Networks

In this paper, we consider the problem of sparse recovery from nonlinear measurements, which has applications in state estimation and bad data detection for power networks. An iterative mixed $\ell_1$ and $\ell_2$ convex program is used to estimate the true state by locally linearizing the nonlinear measurements. When the measurements are linear, through using the almost Euclidean property for a linear subspace, we derive a new performance bound for the state estimation error under sparse bad data and additive observation noise. As a byproduct, in this paper we provide sharp bounds on the almost Euclidean property of a linear subspace, using the "escape-through-the-mesh" theorem from geometric functional analysis. When the measurements are nonlinear, we give conditions under which the solution of the iterative algorithm converges to the true state even though the locally linearized measurements may not be the actual nonlinear measurements. We numerically evaluate our iterative convex programming approach to perform bad data detections in nonlinear electrical power networks problems. We are able to use semidefinite programming to verify the conditions for convergence of the proposed iterative sparse recovery algorithms from nonlinear measurements.