StarCoder 2 and The Stack v2: The Next Generation

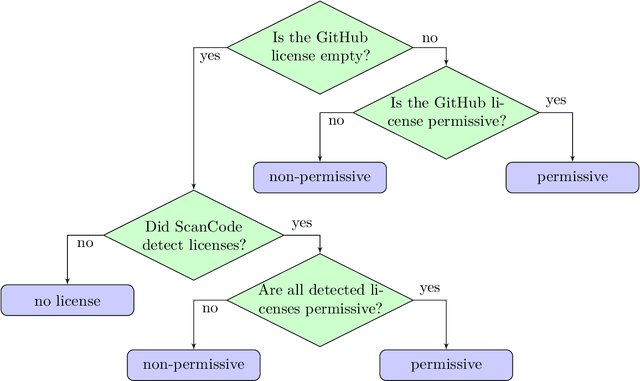
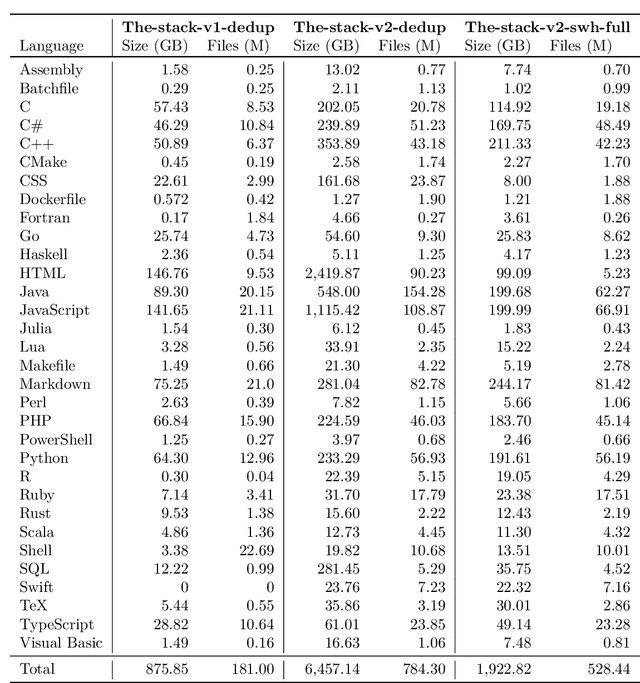
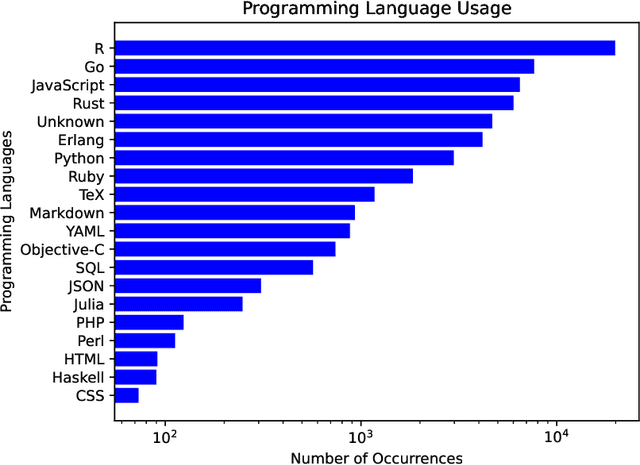
The BigCode project, an open-scientific collaboration focused on the responsible development of Large Language Models for Code (Code LLMs), introduces StarCoder2. In partnership with Software Heritage (SWH), we build The Stack v2 on top of the digital commons of their source code archive. Alongside the SWH repositories spanning 619 programming languages, we carefully select other high-quality data sources, such as GitHub pull requests, Kaggle notebooks, and code documentation. This results in a training set that is 4x larger than the first StarCoder dataset. We train StarCoder2 models with 3B, 7B, and 15B parameters on 3.3 to 4.3 trillion tokens and thoroughly evaluate them on a comprehensive set of Code LLM benchmarks. We find that our small model, StarCoder2-3B, outperforms other Code LLMs of similar size on most benchmarks, and also outperforms StarCoderBase-15B. Our large model, StarCoder2- 15B, significantly outperforms other models of comparable size. In addition, it matches or outperforms CodeLlama-34B, a model more than twice its size. Although DeepSeekCoder- 33B is the best-performing model at code completion for high-resource languages, we find that StarCoder2-15B outperforms it on math and code reasoning benchmarks, as well as several low-resource languages. We make the model weights available under an OpenRAIL license and ensure full transparency regarding the training data by releasing the SoftWare Heritage persistent IDentifiers (SWHIDs) of the source code data.

Optimal Compression for Minimizing Classification Error Probability: an Information-Theoretic Approach

We formulate the problem of performing optimal data compression under the constraints that compressed data can be used for accurate classification in machine learning. We show that this translates to a problem of minimizing the mutual information between data and its compressed version under the constraint on error probability of classification is small when using the compressed data for machine learning. We then provide analytical and computational methods to characterize the optimal trade-off between data compression and classification error probability. First, we provide an analytical characterization for the optimal compression strategy for data with binary labels. Second, for data with multiple labels, we formulate a set of convex optimization problems to characterize the optimal tradeoff, from which the optimal trade-off between the classification error and compression efficiency can be obtained by numerically solving the formulated optimization problems. We further show the improvements of our formulations over the information-bottleneck methods in classification performance.

Task-Aware Network Coding Over Butterfly Network

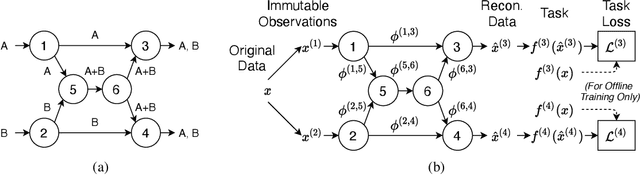
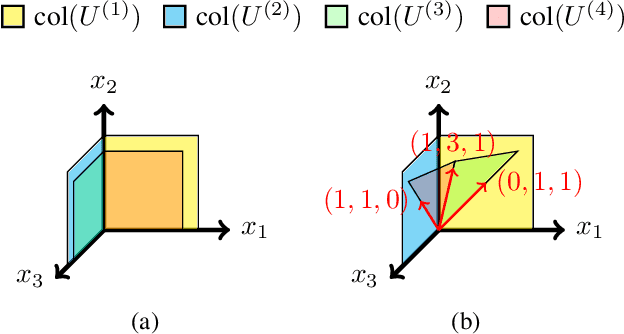
Network coding allows distributed information sources such as sensors to efficiently compress and transmit data to distributed receivers across a bandwidth-limited network. Classical network coding is largely task-agnostic -- the coding schemes mainly aim to faithfully reconstruct data at the receivers, regardless of what ultimate task the received data is used for. In this paper, we analyze a new task-driven network coding problem, where distributed receivers pass transmitted data through machine learning (ML) tasks, which provides an opportunity to improve efficiency by transmitting salient task-relevant data representations. Specifically, we formulate a task-aware network coding problem over a butterfly network in real-coordinate space, where lossy analog compression through principal component analysis (PCA) can be applied. A lower bound for the total loss function for the formulated problem is given, and necessary and sufficient conditions for achieving this lower bound are also provided. We introduce ML algorithms to solve the problem in the general case, and our evaluation demonstrates the effectiveness of task-aware network coding.

Task-aware Privacy Preservation for Multi-dimensional Data

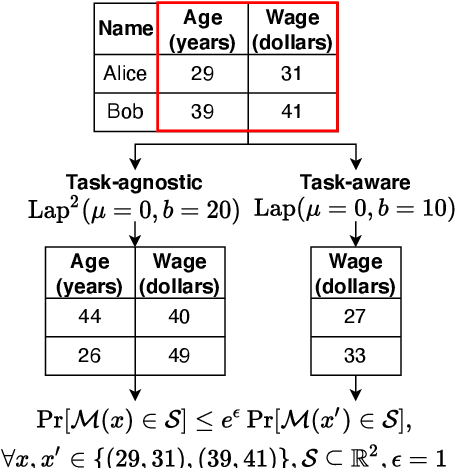
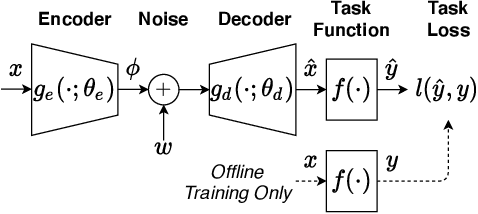
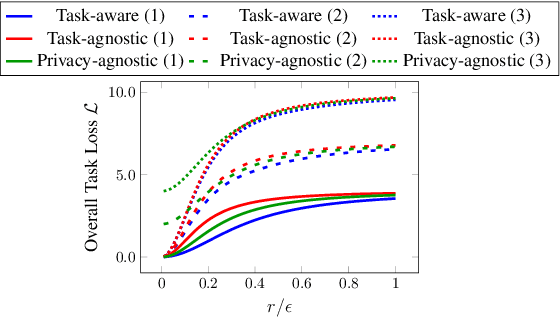
Local differential privacy (LDP), a state-of-the-art technique for privacy preservation, has been successfully deployed in a few real-world applications. In the future, LDP can be adopted to anonymize richer user data attributes that will be input to more sophisticated machine learning (ML) tasks. However, today's LDP approaches are largely task-agnostic and often lead to sub-optimal performance -- they will simply inject noise to all data attributes according to a given privacy budget, regardless of what features are most relevant for an ultimate task. In this paper, we address how to significantly improve the ultimate task performance for multi-dimensional user data by considering a task-aware privacy preservation problem. The key idea is to use an encoder-decoder framework to learn (and anonymize) a task-relevant latent representation of user data, which gives an analytical near-optimal solution for a linear setting with mean-squared error (MSE) task loss. We also provide an approximate solution through a learning algorithm for general nonlinear cases. Extensive experiments demonstrate that our task-aware approach significantly improves ultimate task accuracy compared to a standard benchmark LDP approach while guaranteeing the same level of privacy.

Data Sharing and Compression for Cooperative Networked Control

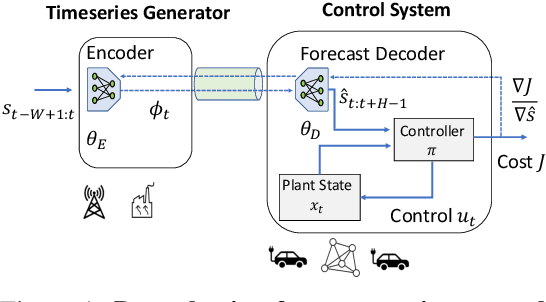
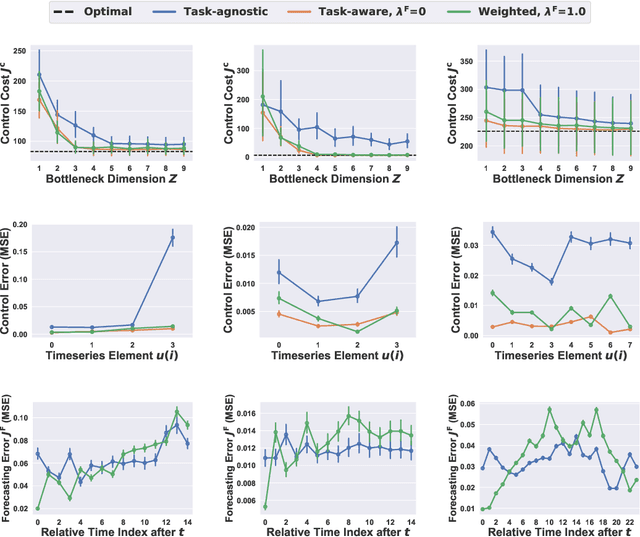
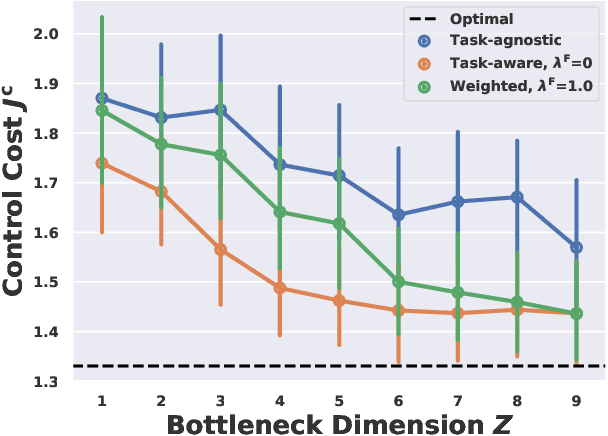
Sharing forecasts of network timeseries data, such as cellular or electricity load patterns, can improve independent control applications ranging from traffic scheduling to power generation. Typically, forecasts are designed without knowledge of a downstream controller's task objective, and thus simply optimize for mean prediction error. However, such task-agnostic representations are often too large to stream over a communication network and do not emphasize salient temporal features for cooperative control. This paper presents a solution to learn succinct, highly-compressed forecasts that are co-designed with a modular controller's task objective. Our simulations with real cellular, Internet-of-Things (IoT), and electricity load data show we can improve a model predictive controller's performance by at least $25\%$ while transmitting $80\%$ less data than the competing method. Further, we present theoretical compression results for a networked variant of the classical linear quadratic regulator (LQR) control problem.

Sparse Recovery from Nonlinear Measurements with Applications in Bad Data Detection for Power Networks

In this paper, we consider the problem of sparse recovery from nonlinear measurements, which has applications in state estimation and bad data detection for power networks. An iterative mixed $\ell_1$ and $\ell_2$ convex program is used to estimate the true state by locally linearizing the nonlinear measurements. When the measurements are linear, through using the almost Euclidean property for a linear subspace, we derive a new performance bound for the state estimation error under sparse bad data and additive observation noise. As a byproduct, in this paper we provide sharp bounds on the almost Euclidean property of a linear subspace, using the "escape-through-the-mesh" theorem from geometric functional analysis. When the measurements are nonlinear, we give conditions under which the solution of the iterative algorithm converges to the true state even though the locally linearized measurements may not be the actual nonlinear measurements. We numerically evaluate our iterative convex programming approach to perform bad data detections in nonlinear electrical power networks problems. We are able to use semidefinite programming to verify the conditions for convergence of the proposed iterative sparse recovery algorithms from nonlinear measurements.