Towards unlocking the mystery of adversarial fragility of neural networks

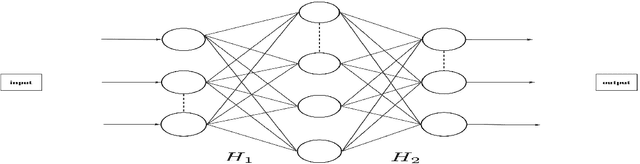
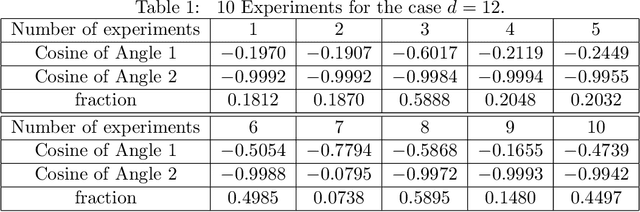
In this paper, we study the adversarial robustness of deep neural networks for classification tasks. We look at the smallest magnitude of possible additive perturbations that can change the output of a classification algorithm. We provide a matrix-theoretic explanation of the adversarial fragility of deep neural network for classification. In particular, our theoretical results show that neural network's adversarial robustness can degrade as the input dimension $d$ increases. Analytically we show that neural networks' adversarial robustness can be only $1/\sqrt{d}$ of the best possible adversarial robustness. Our matrix-theoretic explanation is consistent with an earlier information-theoretic feature-compression-based explanation for the adversarial fragility of neural networks.

Outlier Detection Using Generative Models with Theoretical Performance Guarantees

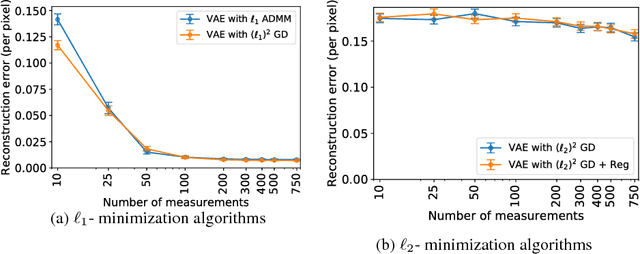
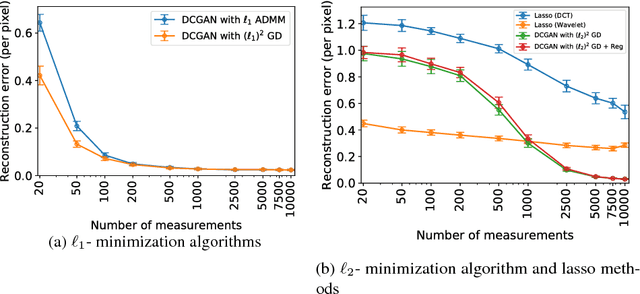
This paper considers the problem of recovering signals modeled by generative models from linear measurements contaminated with sparse outliers. We propose an outlier detection approach for reconstructing the ground-truth signals modeled by generative models under sparse outliers. We establish theoretical recovery guarantees for reconstruction of signals using generative models in the presence of outliers, giving lower bounds on the number of correctable outliers. Our results are applicable to both linear generator neural networks and the nonlinear generator neural networks with an arbitrary number of layers. We propose an iterative alternating direction method of multipliers (ADMM) algorithm for solving the outlier detection problem via $\ell_1$ norm minimization, and a gradient descent algorithm for solving the outlier detection problem via squared $\ell_1$ norm minimization. We conduct extensive experiments using variational auto-encoder and deep convolutional generative adversarial networks, and the experimental results show that the signals can be successfully reconstructed under outliers using our approach. Our approach outperforms the traditional Lasso and $\ell_2$ minimization approach.

Optimal Compression for Minimizing Classification Error Probability: an Information-Theoretic Approach

We formulate the problem of performing optimal data compression under the constraints that compressed data can be used for accurate classification in machine learning. We show that this translates to a problem of minimizing the mutual information between data and its compressed version under the constraint on error probability of classification is small when using the compressed data for machine learning. We then provide analytical and computational methods to characterize the optimal trade-off between data compression and classification error probability. First, we provide an analytical characterization for the optimal compression strategy for data with binary labels. Second, for data with multiple labels, we formulate a set of convex optimization problems to characterize the optimal tradeoff, from which the optimal trade-off between the classification error and compression efficiency can be obtained by numerically solving the formulated optimization problems. We further show the improvements of our formulations over the information-bottleneck methods in classification performance.