Causality-Enhanced Behavior Sequence Modeling in LLMs for Personalized Recommendation

Recent advancements in recommender systems have focused on leveraging Large Language Models (LLMs) to improve user preference modeling, yielding promising outcomes. However, current LLM-based approaches struggle to fully leverage user behavior sequences, resulting in suboptimal preference modeling for personalized recommendations. In this study, we propose a novel Counterfactual Fine-Tuning (CFT) method to address this issue by explicitly emphasizing the role of behavior sequences when generating recommendations. Specifically, we employ counterfactual reasoning to identify the causal effects of behavior sequences on model output and introduce a task that directly fits the ground-truth labels based on these effects, achieving the goal of explicit emphasis. Additionally, we develop a token-level weighting mechanism to adjust the emphasis strength for different item tokens, reflecting the diminishing influence of behavior sequences from earlier to later tokens during predicting an item. Extensive experiments on real-world datasets demonstrate that CFT effectively improves behavior sequence modeling. Our codes are available at https://github.com/itsmeyjt/CFT.

Guaranteed Sampling Flexibility for Low-tubal-rank Tensor Completion

While Bernoulli sampling is extensively studied in tensor completion, t-CUR sampling approximates low-tubal-rank tensors via lateral and horizontal subtensors. However, both methods lack sufficient flexibility for diverse practical applications. To address this, we introduce Tensor Cross-Concentrated Sampling (t-CCS), a novel and straightforward sampling model that advances the matrix cross-concentrated sampling concept within a tensor framework. t-CCS effectively bridges the gap between Bernoulli and t-CUR sampling, offering additional flexibility that can lead to computational savings in various contexts. A key aspect of our work is the comprehensive theoretical analysis provided. We establish a sufficient condition for the successful recovery of a low-rank tensor from its t-CCS samples. In support of this, we also develop a theoretical framework validating the feasibility of t-CUR via uniform random sampling and conduct a detailed theoretical sampling complexity analysis for tensor completion problems utilizing the general Bernoulli sampling model. Moreover, we introduce an efficient non-convex algorithm, the Iterative t-CUR Tensor Completion (ITCURTC) algorithm, specifically designed to tackle the t-CCS-based tensor completion. We have intensively tested and validated the effectiveness of the t-CCS model and the ITCURTC algorithm across both synthetic and real-world datasets.

Accelerating Ill-conditioned Hankel Matrix Recovery via Structured Newton-like Descent

This paper studies the robust Hankel recovery problem, which simultaneously removes the sparse outliers and fulfills missing entries from the partial observation. We propose a novel non-convex algorithm, coined Hankel Structured Newton-Like Descent (HSNLD), to tackle the robust Hankel recovery problem. HSNLD is highly efficient with linear convergence, and its convergence rate is independent of the condition number of the underlying Hankel matrix. The recovery guarantee has been established under some mild conditions. Numerical experiments on both synthetic and real datasets show the superior performance of HSNLD against state-of-the-art algorithms.

An Efficient Two-Stage SPARC Decoder for Massive MIMO Unsourced Random Access

In this paper, we study a concatenate coding scheme based on sparse regression code (SPARC) and tree code for unsourced random access in massive multiple-input and multiple-output (MIMO) systems. Our focus is concentrated on efficient decoding for the inner SPARC with practical concerns. A two-stage method is proposed to achieve near-optimal performance while maintaining low computational complexity. Specifically, an one-step thresholding-based algorithm is first used for reducing large dimensions of the SPARC decoding, after which an relaxed maximum-likelihood estimator is employed for refinement. Adequate simulation results are provided to validate the near-optimal performance and the low computational complexity. Besides, for covariance-based sparse recovery method, theoretical analyses are given to characterize the upper bound of the number of active users supported when convex relaxation is considered, and the probability of successful dimension reduction by the one-step thresholding-based algorithm.

A stochastic alternating minimizing method for sparse phase retrieval

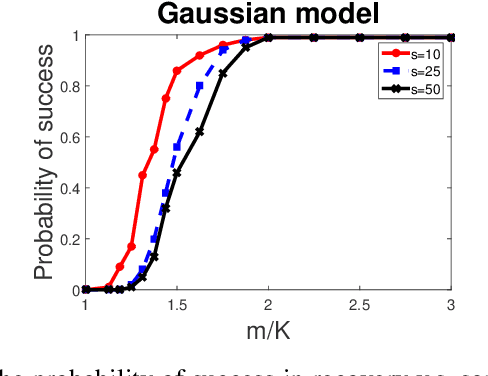
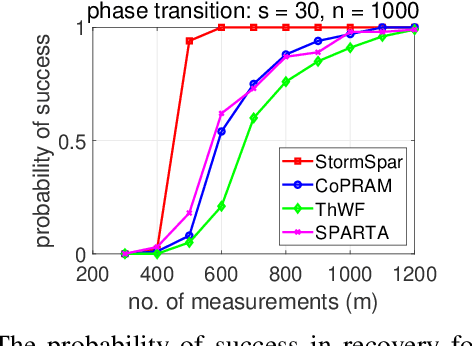
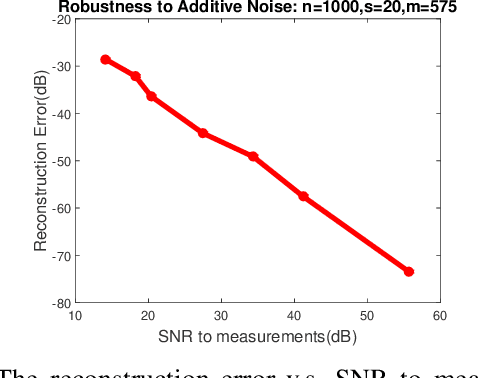
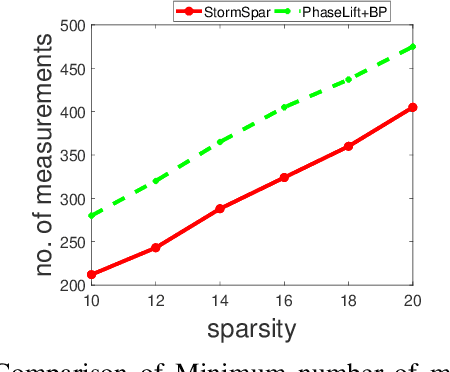
Sparse phase retrieval plays an important role in many fields of applied science and thus attracts lots of attention. In this paper, we propose a \underline{sto}chastic alte\underline{r}nating \underline{m}inimizing method for \underline{sp}arse ph\underline{a}se \underline{r}etrieval (\textit{StormSpar}) algorithm which {emprically} is able to recover $n$-dimensional $s$-sparse signals from only $O(s\,\mathrm{log}\, n)$ number of measurements without a desired initial value required by many existing methods. In \textit{StormSpar}, the hard-thresholding pursuit (HTP) algorithm is employed to solve the sparse constraint least square sub-problems. The main competitive feature of \textit{StormSpar} is that it converges globally requiring optimal order of number of samples with random initialization. Extensive numerical experiments are given to validate the proposed algorithm.