A stochastic alternating minimizing method for sparse phase retrieval
Paper and Code
Jun 14, 2019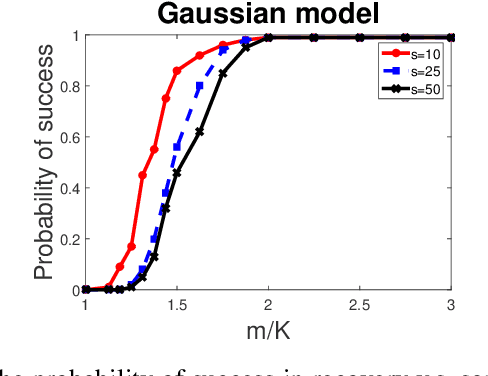
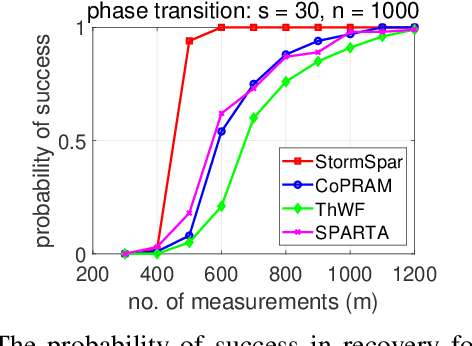
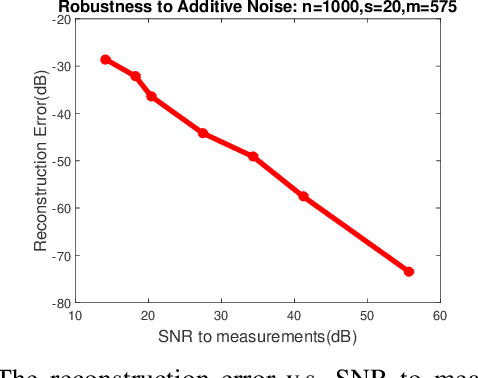
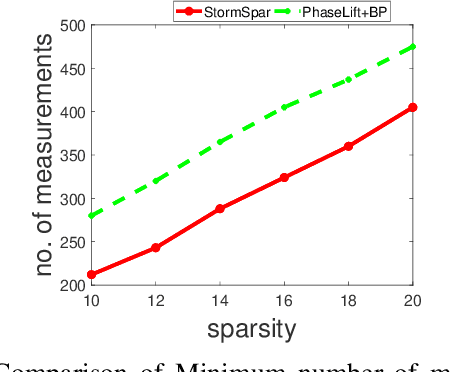
Sparse phase retrieval plays an important role in many fields of applied science and thus attracts lots of attention. In this paper, we propose a \underline{sto}chastic alte\underline{r}nating \underline{m}inimizing method for \underline{sp}arse ph\underline{a}se \underline{r}etrieval (\textit{StormSpar}) algorithm which {emprically} is able to recover $n$-dimensional $s$-sparse signals from only $O(s\,\mathrm{log}\, n)$ number of measurements without a desired initial value required by many existing methods. In \textit{StormSpar}, the hard-thresholding pursuit (HTP) algorithm is employed to solve the sparse constraint least square sub-problems. The main competitive feature of \textit{StormSpar} is that it converges globally requiring optimal order of number of samples with random initialization. Extensive numerical experiments are given to validate the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge