From Nano to Macro: Overview of the IEEE Bio Image and Signal Processing Technical Committee

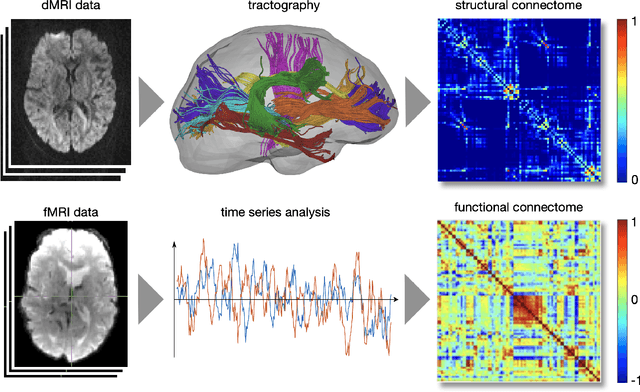
The Bio Image and Signal Processing (BISP) Technical Committee (TC) of the IEEE Signal Processing Society (SPS) promotes activities within the broad technical field of biomedical image and signal processing. Areas of interest include medical and biological imaging, digital pathology, molecular imaging, microscopy, and associated computational imaging, image analysis, and image-guided treatment, alongside physiological signal processing, computational biology, and bioinformatics. BISP has 40 members and covers a wide range of EDICS, including CIS-MI: Medical Imaging, BIO-MIA: Medical Image Analysis, BIO-BI: Biological Imaging, BIO: Biomedical Signal Processing, BIO-BCI: Brain/Human-Computer Interfaces, and BIO-INFR: Bioinformatics. BISP plays a central role in the organization of the IEEE International Symposium on Biomedical Imaging (ISBI) and contributes to the technical sessions at the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), and the IEEE International Conference on Image Processing (ICIP). In this paper, we provide a brief history of the TC, review the technological and methodological contributions its community delivered, and highlight promising new directions we anticipate.

Vector-Valued Graph Trend Filtering with Non-Convex Penalties

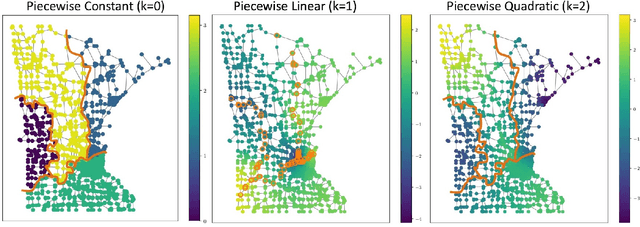
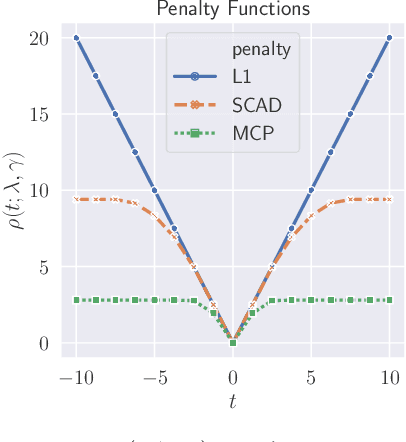
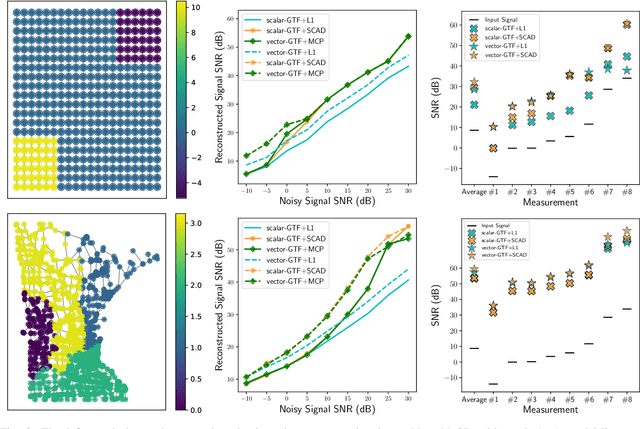
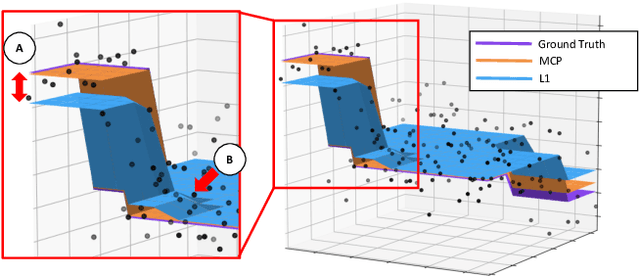
We study the denoising of piecewise smooth graph signals that exhibit inhomogeneous levels of smoothness over a graph, where the value at each node can be vector-valued. We extend the graph trend filtering framework to denoising vector-valued graph signals with a family of non-convex regularizers that exhibit superior recovery performance over existing convex regularizers. We establish the statistical error rates of first-order stationary points of the proposed non-convex method for generic graphs using oracle inequalities. We further present an ADMM-based algorithm to solve the proposed method and analyze its convergence. We present numerical experiments on both synthetic and real-world data for denoising, support recovery, and semi-supervised classification.

Sampling Theory for Graph Signals on Product Graphs

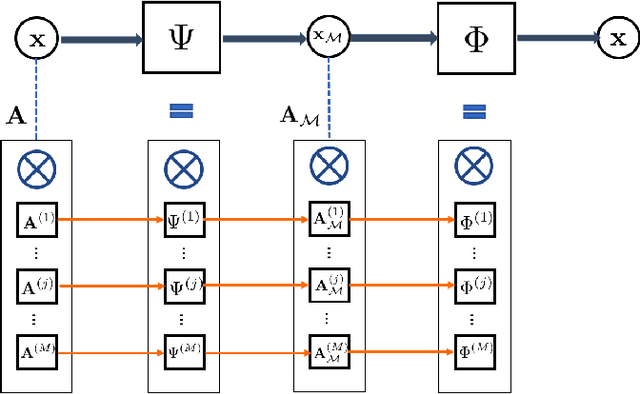
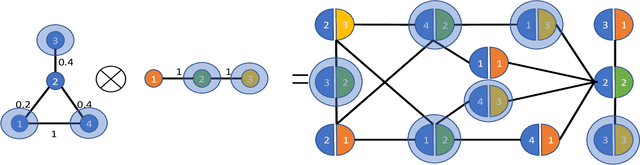
In this paper, we extend the sampling theory on graphs by constructing a framework that exploits the structure in product graphs for efficient sampling and recovery of bandlimited graph signals that lie on them. Product graphs are graphs that are composed from smaller graph atoms; we motivate how this model is a flexible and useful way to model richer classes of data that can be multi-modal in nature. Previous works have established a sampling theory on graphs for bandlimited signals. Importantly, the framework achieves significant savings in both sample complexity and computational complexity

Generalized Value Iteration Networks: Life Beyond Lattices

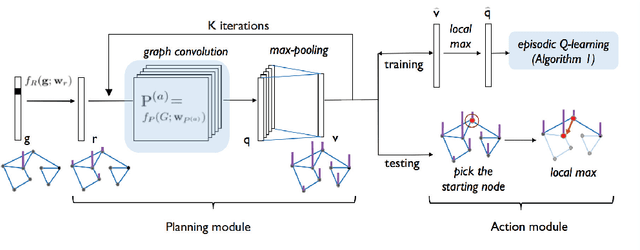
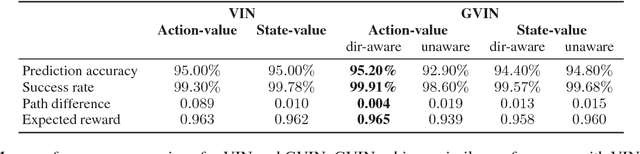
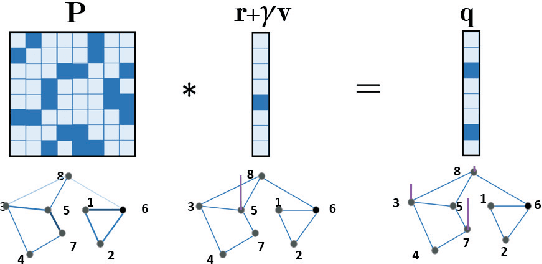
In this paper, we introduce a generalized value iteration network (GVIN), which is an end-to-end neural network planning module. GVIN emulates the value iteration algorithm by using a novel graph convolution operator, which enables GVIN to learn and plan on irregular spatial graphs. We propose three novel differentiable kernels as graph convolution operators and show that the embedding based kernel achieves the best performance. We further propose episodic Q-learning, an improvement upon traditional n-step Q-learning that stabilizes training for networks that contain a planning module. Lastly, we evaluate GVIN on planning problems in 2D mazes, irregular graphs, and real-world street networks, showing that GVIN generalizes well for both arbitrary graphs and unseen graphs of larger scale and outperforms a naive generalization of VIN (discretizing a spatial graph into a 2D image).

Fast Resampling of 3D Point Clouds via Graphs

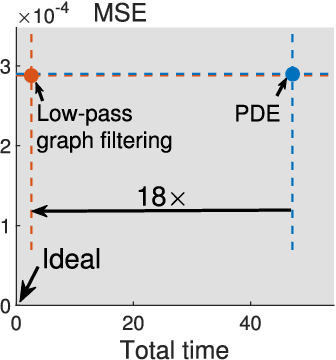
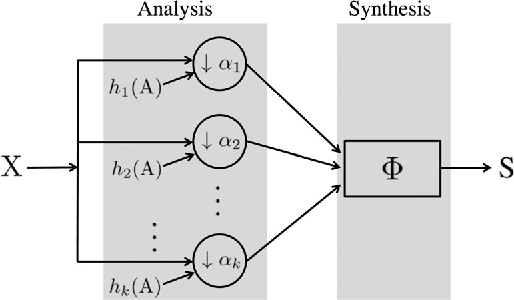
To reduce cost in storing, processing and visualizing a large-scale point cloud, we consider a randomized resampling strategy to select a representative subset of points while preserving application-dependent features. The proposed strategy is based on graphs, which can represent underlying surfaces and lend themselves well to efficient computation. We use a general feature-extraction operator to represent application-dependent features and propose a general reconstruction error to evaluate the quality of resampling. We obtain a general form of optimal resampling distribution by minimizing the reconstruction error. The proposed optimal resampling distribution is guaranteed to be shift, rotation and scale-invariant in the 3D space. We next specify the feature-extraction operator to be a graph filter and study specific resampling strategies based on all-pass, low-pass, high-pass graph filtering and graph filter banks. We finally apply the proposed methods to three applications: large-scale visualization, accurate registration and robust shape modeling. The empirical performance validates the effectiveness and efficiency of the proposed resampling methods.

A statistical perspective of sampling scores for linear regression

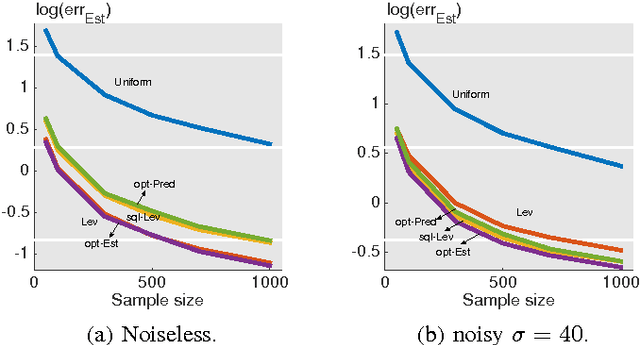
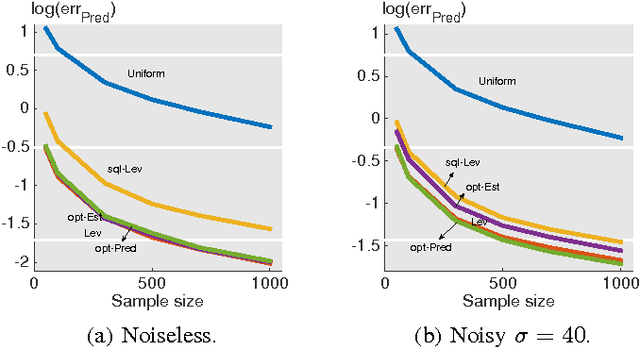
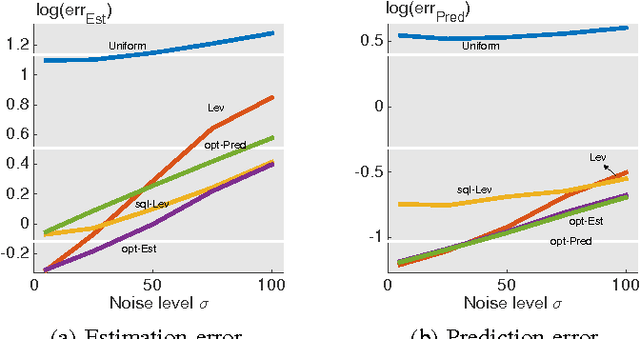
In this paper, we consider a statistical problem of learning a linear model from noisy samples. Existing work has focused on approximating the least squares solution by using leverage-based scores as an importance sampling distribution. However, no finite sample statistical guarantees and no computationally efficient optimal sampling strategies have been proposed. To evaluate the statistical properties of different sampling strategies, we propose a simple yet effective estimator, which is easy for theoretical analysis and is useful in multitask linear regression. We derive the exact mean square error of the proposed estimator for any given sampling scores. Based on minimizing the mean square error, we propose the optimal sampling scores for both estimator and predictor, and show that they are influenced by the noise-to-signal ratio. Numerical simulations match the theoretical analysis well.

Signal Representations on Graphs: Tools and Applications

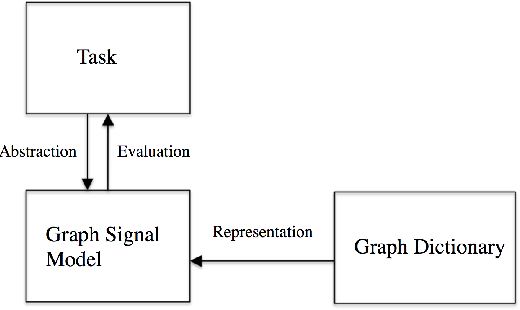
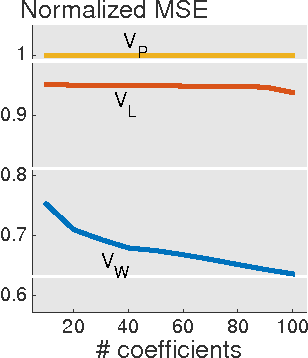
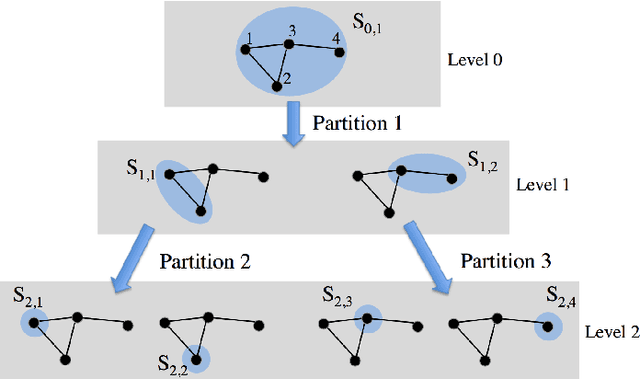
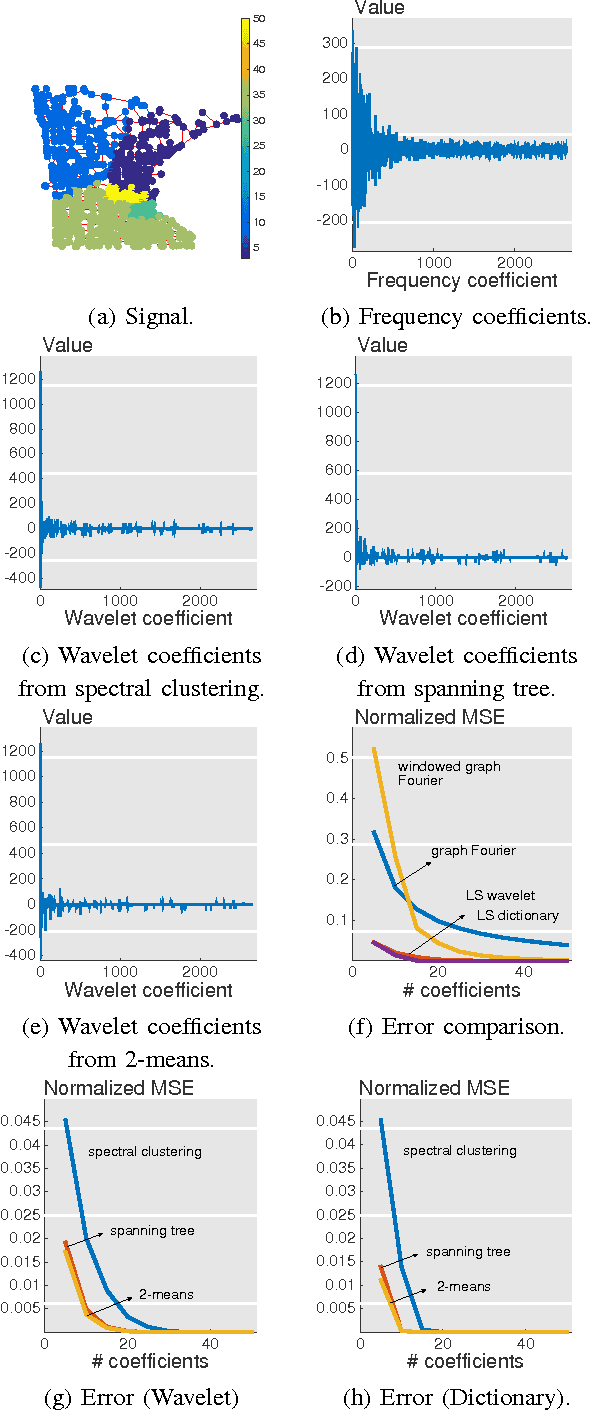
We present a framework for representing and modeling data on graphs. Based on this framework, we study three typical classes of graph signals: smooth graph signals, piecewise-constant graph signals, and piecewise-smooth graph signals. For each class, we provide an explicit definition of the graph signals and construct a corresponding graph dictionary with desirable properties. We then study how such graph dictionary works in two standard tasks: approximation and sampling followed with recovery, both from theoretical as well as algorithmic perspectives. Finally, for each class, we present a case study of a real-world problem by using the proposed methodology.

Image Classification with Rejection using Contextual Information

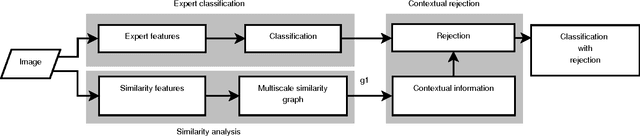
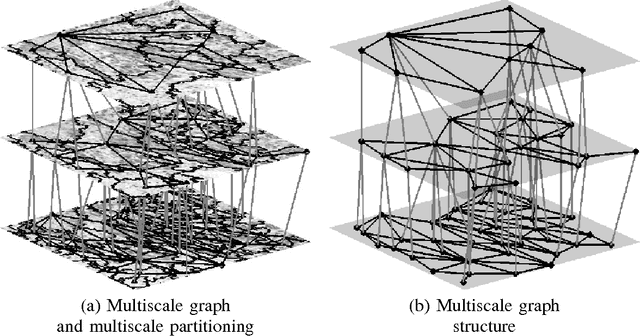
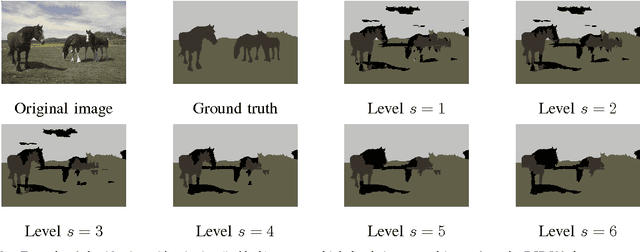
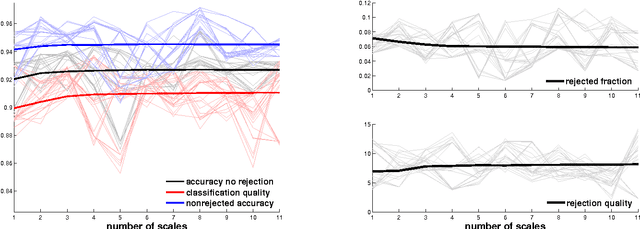
We introduce a new supervised algorithm for image classification with rejection using multiscale contextual information. Rejection is desired in image-classification applications that require a robust classifier but not the classification of the entire image. The proposed algorithm combines local and multiscale contextual information with rejection, improving the classification performance. As a probabilistic model for classification, we adopt a multinomial logistic regression. The concept of rejection with contextual information is implemented by modeling the classification problem as an energy minimization problem over a graph representing local and multiscale similarities of the image. The rejection is introduced through an energy data term associated with the classification risk and the contextual information through an energy smoothness term associated with the local and multiscale similarities within the image. We illustrate the proposed method on the classification of images of H&E-stained teratoma tissues.

Signal Recovery on Graphs: Variation Minimization

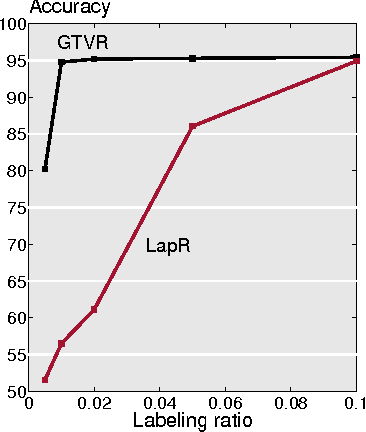
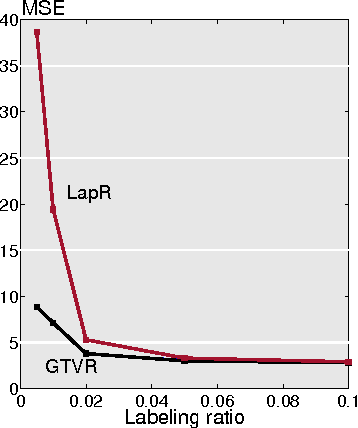
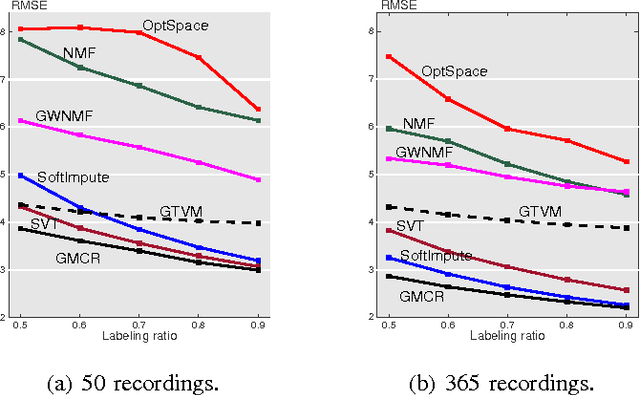
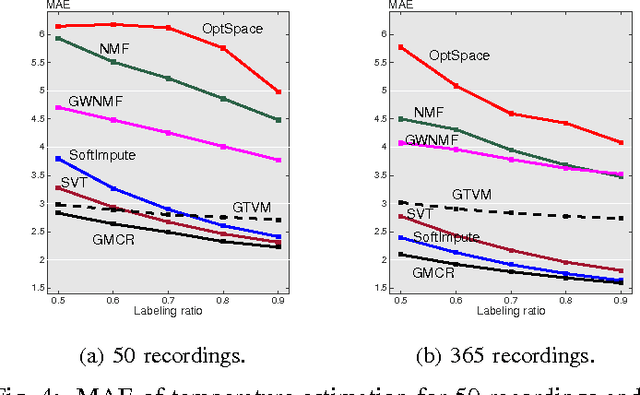
We consider the problem of signal recovery on graphs as graphs model data with complex structure as signals on a graph. Graph signal recovery implies recovery of one or multiple smooth graph signals from noisy, corrupted, or incomplete measurements. We propose a graph signal model and formulate signal recovery as a corresponding optimization problem. We provide a general solution by using the alternating direction methods of multipliers. We next show how signal inpainting, matrix completion, robust principal component analysis, and anomaly detection all relate to graph signal recovery, and provide corresponding specific solutions and theoretical analysis. Finally, we validate the proposed methods on real-world recovery problems, including online blog classification, bridge condition identification, temperature estimation, recommender system, and expert opinion combination of online blog classification.

Signal Recovery on Graphs: Random versus Experimentally Designed Sampling

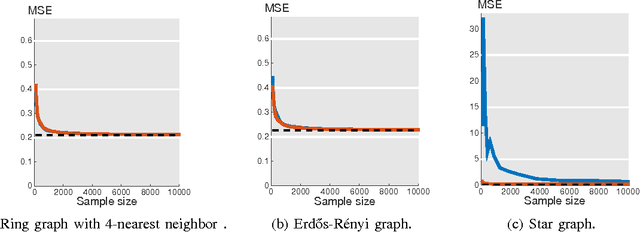
We study signal recovery on graphs based on two sampling strategies: random sampling and experimentally designed sampling. We propose a new class of smooth graph signals, called approximately bandlimited, which generalizes the bandlimited class and is similar to the globally smooth class. We then propose two recovery strategies based on random sampling and experimentally designed sampling. The proposed recovery strategy based on experimentally designed sampling is similar to the leverage scores used in the matrix approximation. We show that while both strategies are unbiased estimators for the low-frequency components, the convergence rate of experimentally designed sampling is much faster than that of random sampling when a graph is irregular. We validate the proposed recovery strategies on three specific graphs: a ring graph, an Erd\H{o}s-R\'enyi graph, and a star graph. The simulation results support the theoretical analysis.