Vector-Valued Graph Trend Filtering with Non-Convex Penalties

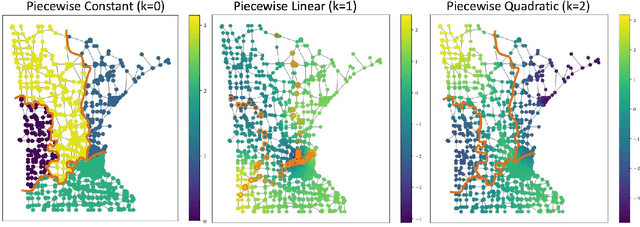
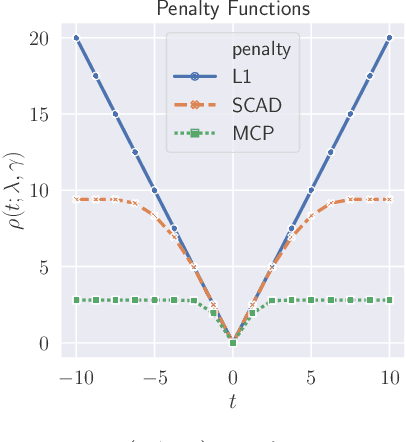
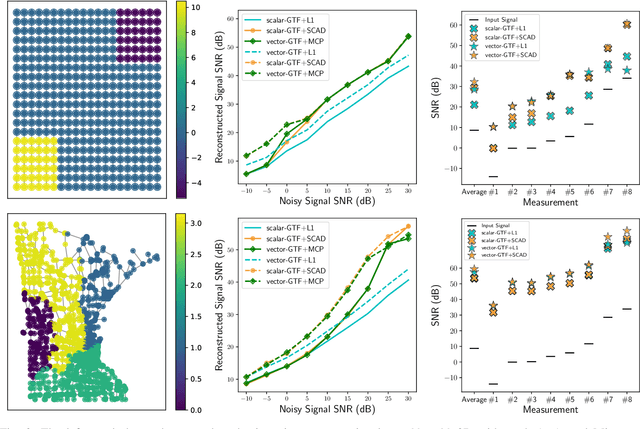
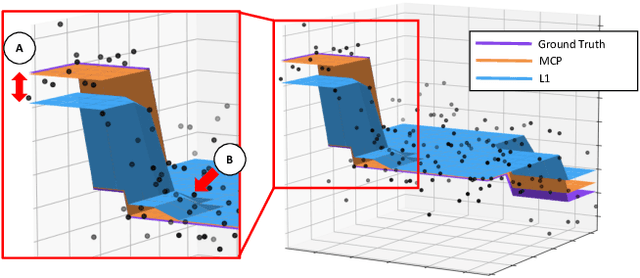
We study the denoising of piecewise smooth graph signals that exhibit inhomogeneous levels of smoothness over a graph, where the value at each node can be vector-valued. We extend the graph trend filtering framework to denoising vector-valued graph signals with a family of non-convex regularizers that exhibit superior recovery performance over existing convex regularizers. We establish the statistical error rates of first-order stationary points of the proposed non-convex method for generic graphs using oracle inequalities. We further present an ADMM-based algorithm to solve the proposed method and analyze its convergence. We present numerical experiments on both synthetic and real-world data for denoising, support recovery, and semi-supervised classification.