Signal Representations on Graphs: Tools and Applications
Paper and Code
Dec 16, 2015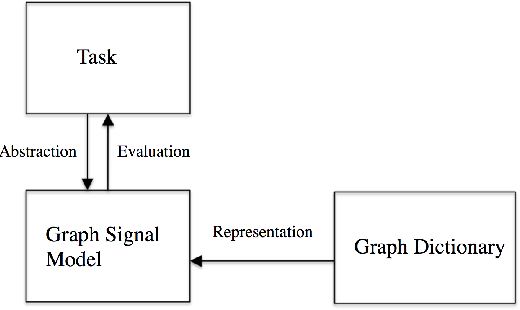
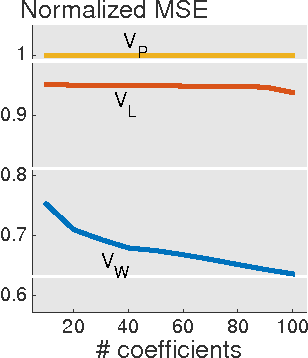
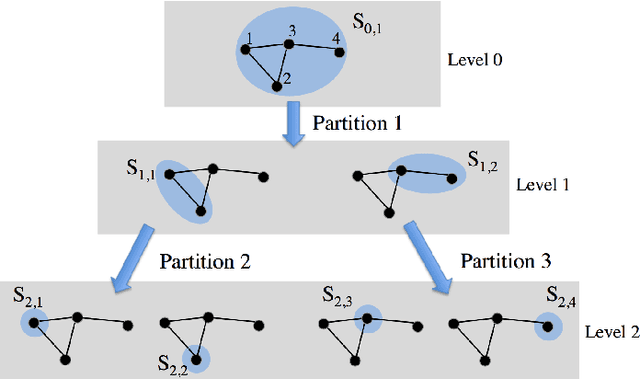
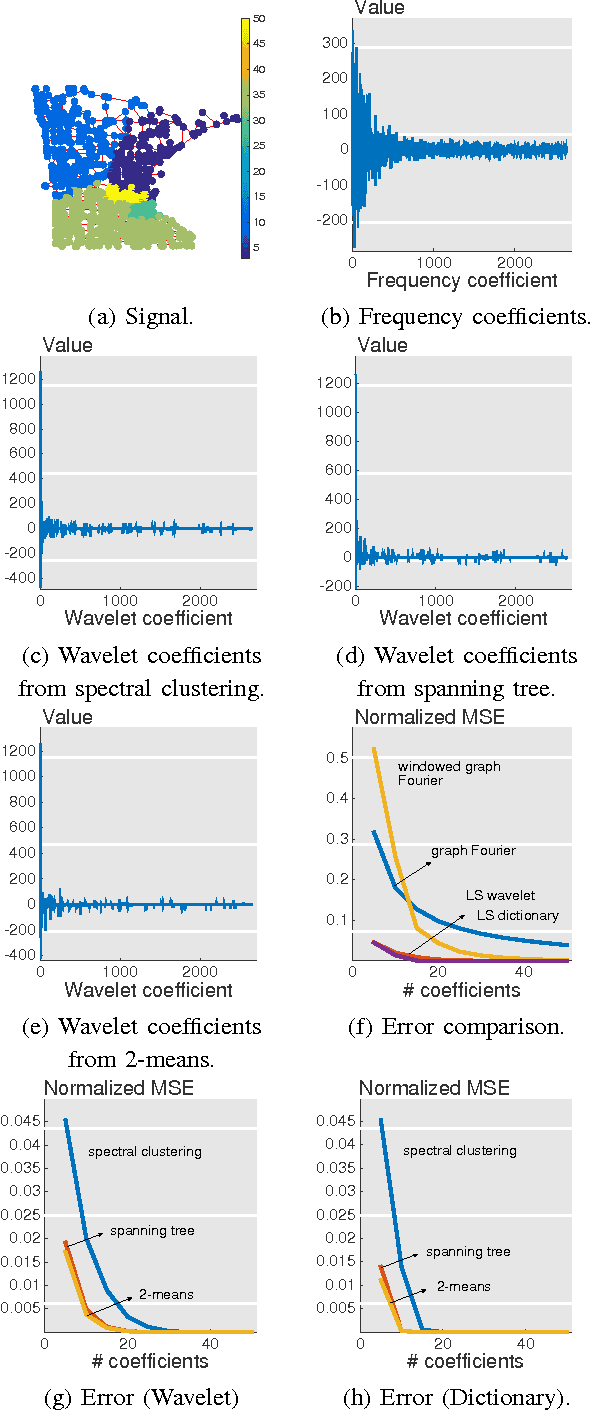
We present a framework for representing and modeling data on graphs. Based on this framework, we study three typical classes of graph signals: smooth graph signals, piecewise-constant graph signals, and piecewise-smooth graph signals. For each class, we provide an explicit definition of the graph signals and construct a corresponding graph dictionary with desirable properties. We then study how such graph dictionary works in two standard tasks: approximation and sampling followed with recovery, both from theoretical as well as algorithmic perspectives. Finally, for each class, we present a case study of a real-world problem by using the proposed methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge