A statistical perspective of sampling scores for linear regression
Paper and Code
Feb 10, 2016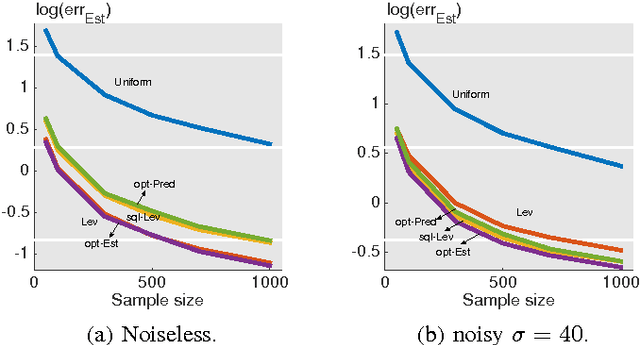
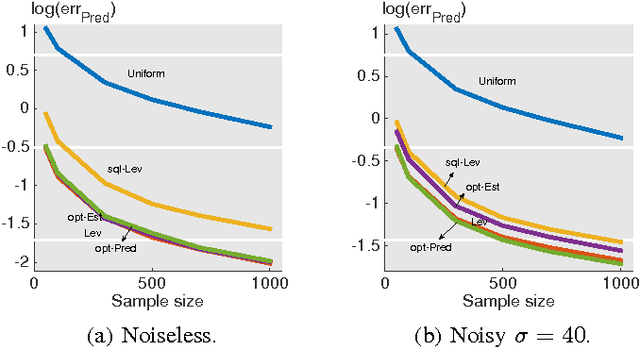
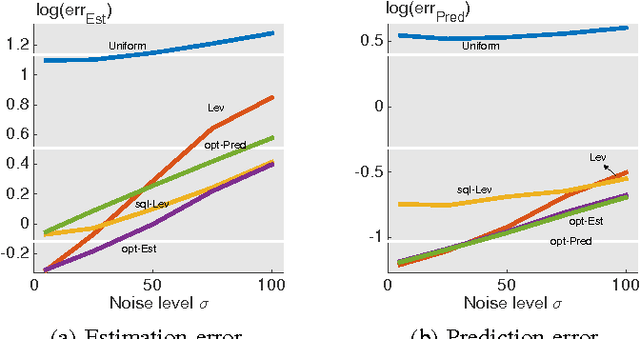
In this paper, we consider a statistical problem of learning a linear model from noisy samples. Existing work has focused on approximating the least squares solution by using leverage-based scores as an importance sampling distribution. However, no finite sample statistical guarantees and no computationally efficient optimal sampling strategies have been proposed. To evaluate the statistical properties of different sampling strategies, we propose a simple yet effective estimator, which is easy for theoretical analysis and is useful in multitask linear regression. We derive the exact mean square error of the proposed estimator for any given sampling scores. Based on minimizing the mean square error, we propose the optimal sampling scores for both estimator and predictor, and show that they are influenced by the noise-to-signal ratio. Numerical simulations match the theoretical analysis well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge