Signal Recovery on Graphs: Random versus Experimentally Designed Sampling

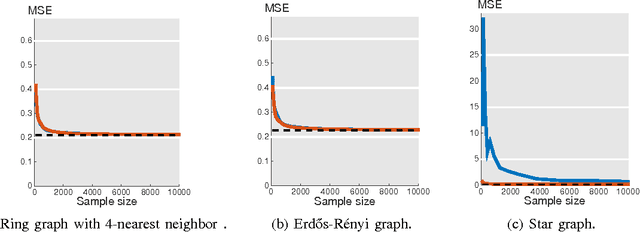
We study signal recovery on graphs based on two sampling strategies: random sampling and experimentally designed sampling. We propose a new class of smooth graph signals, called approximately bandlimited, which generalizes the bandlimited class and is similar to the globally smooth class. We then propose two recovery strategies based on random sampling and experimentally designed sampling. The proposed recovery strategy based on experimentally designed sampling is similar to the leverage scores used in the matrix approximation. We show that while both strategies are unbiased estimators for the low-frequency components, the convergence rate of experimentally designed sampling is much faster than that of random sampling when a graph is irregular. We validate the proposed recovery strategies on three specific graphs: a ring graph, an Erd\H{o}s-R\'enyi graph, and a star graph. The simulation results support the theoretical analysis.