Hsueh-Ti Derek Liu
CageNet: A Meta-Framework for Learning on Wild Meshes
May 24, 2025Abstract:Learning on triangle meshes has recently proven to be instrumental to a myriad of tasks, from shape classification, to segmentation, to deformation and animation, to mention just a few. While some of these applications are tackled through neural network architectures which are tailored to the application at hand, many others use generic frameworks for triangle meshes where the only customization required is the modification of the input features and the loss function. Our goal in this paper is to broaden the applicability of these generic frameworks to "wild", i.e. meshes in-the-wild which often have multiple components, non-manifold elements, disrupted connectivity, or a combination of these. We propose a configurable meta-framework based on the concept of caged geometry: Given a mesh, a cage is a single component manifold triangle mesh that envelopes it closely. Generalized barycentric coordinates map between functions on the cage, and functions on the mesh, allowing us to learn and test on a variety of data, in different applications. We demonstrate this concept by learning segmentation and skinning weights on difficult data, achieving better performance to state of the art techniques on wild meshes.
* 11 pages, 13 figures (excluding supplementary material)
Efficient Autoregressive Shape Generation via Octree-Based Adaptive Tokenization
Apr 03, 2025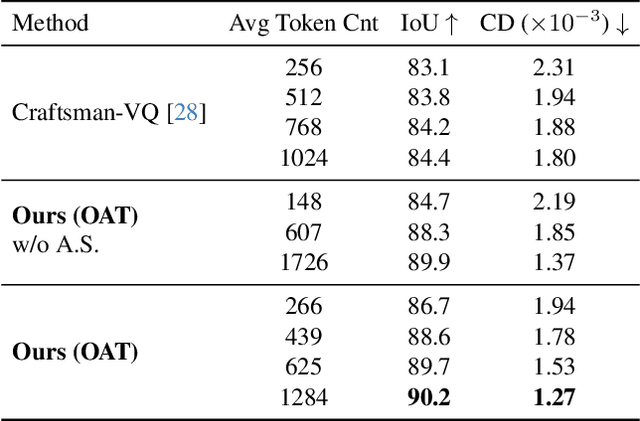

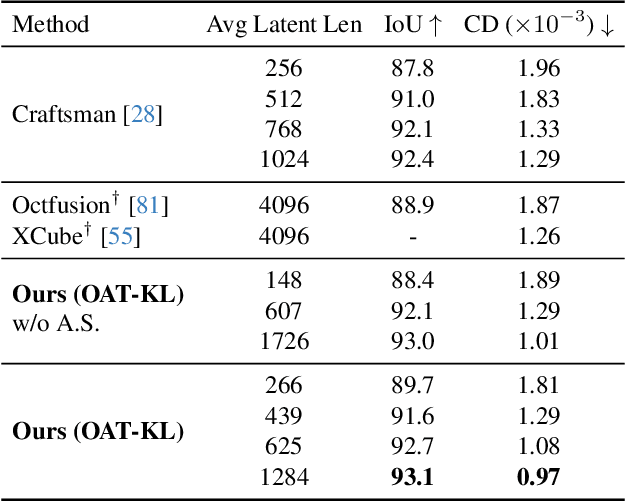
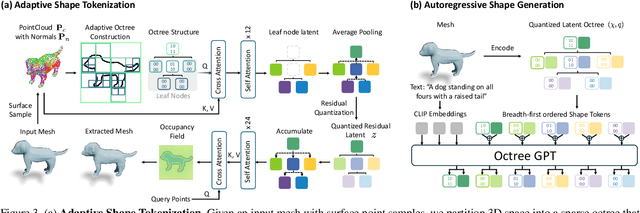
Abstract:Many 3D generative models rely on variational autoencoders (VAEs) to learn compact shape representations. However, existing methods encode all shapes into a fixed-size token, disregarding the inherent variations in scale and complexity across 3D data. This leads to inefficient latent representations that can compromise downstream generation. We address this challenge by introducing Octree-based Adaptive Tokenization, a novel framework that adjusts the dimension of latent representations according to shape complexity. Our approach constructs an adaptive octree structure guided by a quadric-error-based subdivision criterion and allocates a shape latent vector to each octree cell using a query-based transformer. Building upon this tokenization, we develop an octree-based autoregressive generative model that effectively leverages these variable-sized representations in shape generation. Extensive experiments demonstrate that our approach reduces token counts by 50% compared to fixed-size methods while maintaining comparable visual quality. When using a similar token length, our method produces significantly higher-quality shapes. When incorporated with our downstream generative model, our method creates more detailed and diverse 3D content than existing approaches.
A Unified Differentiable Boolean Operator with Fuzzy Logic
Jul 15, 2024Abstract:This paper presents a unified differentiable boolean operator for implicit solid shape modeling using Constructive Solid Geometry (CSG). Traditional CSG relies on min, max operators to perform boolean operations on implicit shapes. But because these boolean operators are discontinuous and discrete in the choice of operations, this makes optimization over the CSG representation challenging. Drawing inspiration from fuzzy logic, we present a unified boolean operator that outputs a continuous function and is differentiable with respect to operator types. This enables optimization of both the primitives and the boolean operations employed in CSG with continuous optimization techniques, such as gradient descent. We further demonstrate that such a continuous boolean operator allows modeling of both sharp mechanical objects and smooth organic shapes with the same framework. Our proposed boolean operator opens up new possibilities for future research toward fully continuous CSG optimization.
An Intrinsic Vector Heat Network
Jun 14, 2024Abstract:Vector fields are widely used to represent and model flows for many science and engineering applications. This paper introduces a novel neural network architecture for learning tangent vector fields that are intrinsically defined on manifold surfaces embedded in 3D. Previous approaches to learning vector fields on surfaces treat vectors as multi-dimensional scalar fields, using traditional scalar-valued architectures to process channels individually, thus fail to preserve fundamental intrinsic properties of the vector field. The core idea of this work is to introduce a trainable vector heat diffusion module to spatially propagate vector-valued feature data across the surface, which we incorporate into our proposed architecture that consists of vector-valued neurons. Our architecture is invariant to rigid motion of the input, isometric deformation, and choice of local tangent bases, and is robust to discretizations of the surface. We evaluate our Vector Heat Network on triangle meshes, and empirically validate its invariant properties. We also demonstrate the effectiveness of our method on the useful industrial application of quadrilateral mesh generation.
Learning Smooth Neural Functions via Lipschitz Regularization
Feb 16, 2022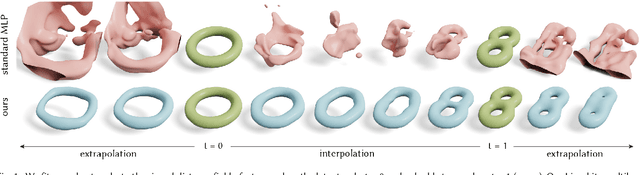

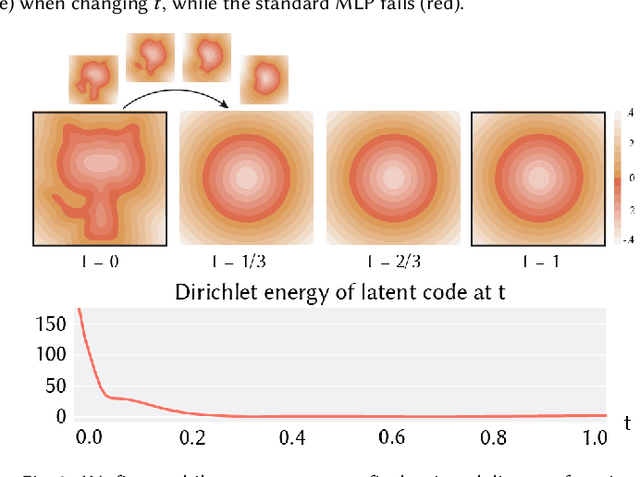

Abstract:Neural implicit fields have recently emerged as a useful representation for 3D shapes. These fields are commonly represented as neural networks which map latent descriptors and 3D coordinates to implicit function values. The latent descriptor of a neural field acts as a deformation handle for the 3D shape it represents. Thus, smoothness with respect to this descriptor is paramount for performing shape-editing operations. In this work, we introduce a novel regularization designed to encourage smooth latent spaces in neural fields by penalizing the upper bound on the field's Lipschitz constant. Compared with prior Lipschitz regularized networks, ours is computationally fast, can be implemented in four lines of code, and requires minimal hyperparameter tuning for geometric applications. We demonstrate the effectiveness of our approach on shape interpolation and extrapolation as well as partial shape reconstruction from 3D point clouds, showing both qualitative and quantitative improvements over existing state-of-the-art and non-regularized baselines.
Neural Subdivision
May 04, 2020
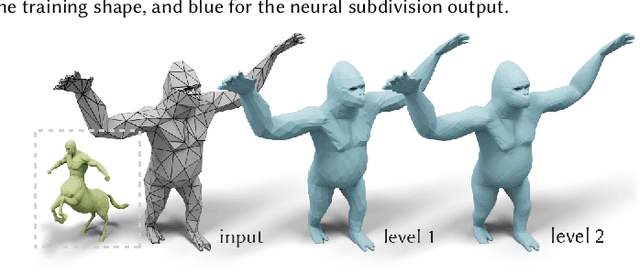
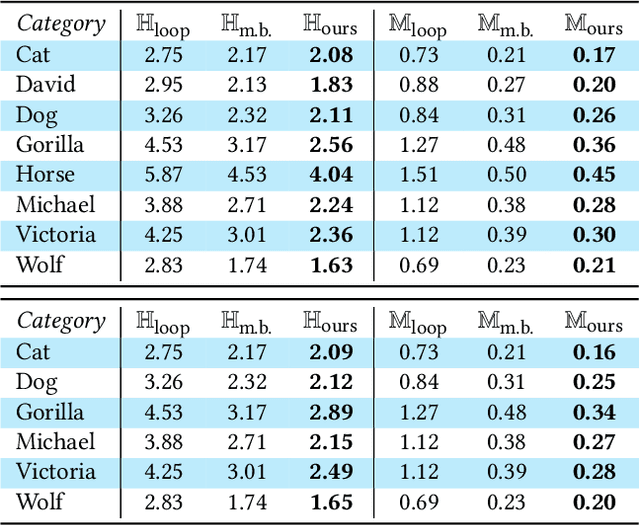
Abstract:This paper introduces Neural Subdivision, a novel framework for data-driven coarse-to-fine geometry modeling. During inference, our method takes a coarse triangle mesh as input and recursively subdivides it to a finer geometry by applying the fixed topological updates of Loop Subdivision, but predicting vertex positions using a neural network conditioned on the local geometry of a patch. This approach enables us to learn complex non-linear subdivision schemes, beyond simple linear averaging used in classical techniques. One of our key contributions is a novel self-supervised training setup that only requires a set of high-resolution meshes for learning network weights. For any training shape, we stochastically generate diverse low-resolution discretizations of coarse counterparts, while maintaining a bijective mapping that prescribes the exact target position of every new vertex during the subdivision process. This leads to a very efficient and accurate loss function for conditional mesh generation, and enables us to train a method that generalizes across discretizations and favors preserving the manifold structure of the output. During training we optimize for the same set of network weights across all local mesh patches, thus providing an architecture that is not constrained to a specific input mesh, fixed genus, or category. Our network encodes patch geometry in a local frame in a rotation- and translation-invariant manner. Jointly, these design choices enable our method to generalize well, and we demonstrate that even when trained on a single high-resolution mesh our method generates reasonable subdivisions for novel shapes.
* 16 pages
Adversarial Geometry and Lighting using a Differentiable Renderer
Aug 08, 2018

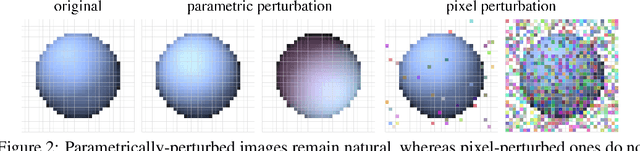

Abstract:Many machine learning classifiers are vulnerable to adversarial attacks, inputs with perturbations designed to intentionally trigger misclassification. Modern adversarial methods either directly alter pixel colors, or "paint" colors onto a 3D shapes. We propose novel adversarial attacks that directly alter the geometry of 3D objects and/or manipulate the lighting in a virtual scene. We leverage a novel differentiable renderer that is efficient to evaluate and analytically differentiate. Our renderer generates images realistic enough for correct classification by common pre-trained models, and we use it to design physical adversarial examples that consistently fool these models. We conduct qualitative and quantitate experiments to validate our adversarial geometry and adversarial lighting attack capabilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge