Adversarial Geometry and Lighting using a Differentiable Renderer

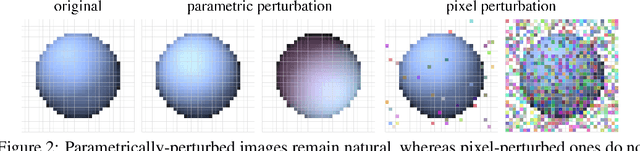
Many machine learning classifiers are vulnerable to adversarial attacks, inputs with perturbations designed to intentionally trigger misclassification. Modern adversarial methods either directly alter pixel colors, or "paint" colors onto a 3D shapes. We propose novel adversarial attacks that directly alter the geometry of 3D objects and/or manipulate the lighting in a virtual scene. We leverage a novel differentiable renderer that is efficient to evaluate and analytically differentiate. Our renderer generates images realistic enough for correct classification by common pre-trained models, and we use it to design physical adversarial examples that consistently fool these models. We conduct qualitative and quantitate experiments to validate our adversarial geometry and adversarial lighting attack capabilities.

An empirical analysis of the optimization of deep network loss surfaces

The success of deep neural networks hinges on our ability to accurately and efficiently optimize high-dimensional, non-convex functions. In this paper, we empirically investigate the loss functions of state-of-the-art networks, and how commonly-used stochastic gradient descent variants optimize these loss functions. To do this, we visualize the loss function by projecting them down to low-dimensional spaces chosen based on the convergence points of different optimization algorithms. Our observations suggest that optimization algorithms encounter and choose different descent directions at many saddle points to find different final weights. Based on consistency we observe across re-runs of the same stochastic optimization algorithm, we hypothesize that each optimization algorithm makes characteristic choices at these saddle points.