Model Predictive Control via On-Policy Imitation Learning

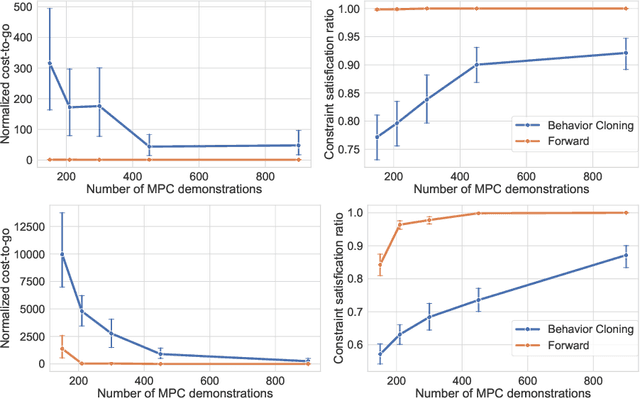
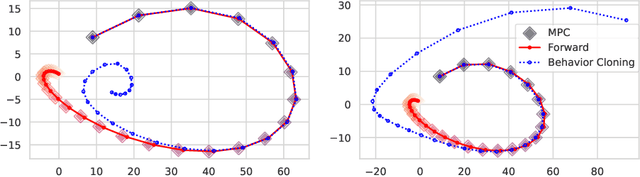
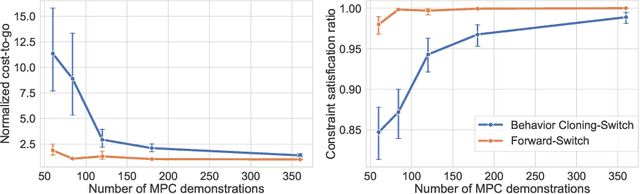
In this paper, we leverage the rapid advances in imitation learning, a topic of intense recent focus in the Reinforcement Learning (RL) literature, to develop new sample complexity results and performance guarantees for data-driven Model Predictive Control (MPC) for constrained linear systems. In its simplest form, imitation learning is an approach that tries to learn an expert policy by querying samples from an expert. Recent approaches to data-driven MPC have used the simplest form of imitation learning known as behavior cloning to learn controllers that mimic the performance of MPC by online sampling of the trajectories of the closed-loop MPC system. Behavior cloning, however, is a method that is known to be data inefficient and suffer from distribution shifts. As an alternative, we develop a variant of the forward training algorithm which is an on-policy imitation learning method proposed by Ross et al. (2010). Our algorithm uses the structure of constrained linear MPC, and our analysis uses the properties of the explicit MPC solution to theoretically bound the number of online MPC trajectories needed to achieve optimal performance. We validate our results through simulations and show that the forward training algorithm is indeed superior to behavior cloning when applied to MPC.

Time varying regression with hidden linear dynamics

We revisit a model for time-varying linear regression that assumes the unknown parameters evolve according to a linear dynamical system. Counterintuitively, we show that when the underlying dynamics are stable the parameters of this model can be estimated from data by combining just two ordinary least squares estimates. We offer a finite sample guarantee on the estimation error of our method and discuss certain advantages it has over Expectation-Maximization (EM), which is the main approach proposed by prior work.

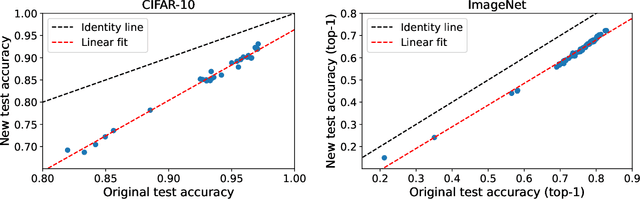
Why do classifier accuracies show linear trends under distribution shift?

Several recent studies observed that when classification models are evaluated on two different data distributions, the models' accuracies on one distribution are approximately a linear function of their accuracies on another distribution. We offer an explanation for these observations based on two assumptions that can be assessed empirically: (1) certain events have similar probabilities under the two distributions; (2) the probability that a lower accuracy model correctly classifies a data point sampled from one distribution when a higher accuracy model classifies it incorrectly is small.

Bandit Learning in Decentralized Matching Markets

We study two-sided matching markets in which one side of the market (the players) does not have a priori knowledge about its preferences for the other side (the arms) and is required to learn its preferences from experience. Also, we assume the players have no direct means of communication. This model extends the standard stochastic multi-armed bandit framework to a decentralized multiple player setting with competition. We introduce a new algorithm for this setting that, over a time horizon $T$, attains $\mathcal{O}(\log(T))$ stable regret when preferences of the arms over players are shared, and $\mathcal{O}(\log(T)^2)$ regret when there are no assumptions on the preferences on either side.

Active Learning for Nonlinear System Identification with Guarantees

While the identification of nonlinear dynamical systems is a fundamental building block of model-based reinforcement learning and feedback control, its sample complexity is only understood for systems that either have discrete states and actions or for systems that can be identified from data generated by i.i.d. random inputs. Nonetheless, many interesting dynamical systems have continuous states and actions and can only be identified through a judicious choice of inputs. Motivated by practical settings, we study a class of nonlinear dynamical systems whose state transitions depend linearly on a known feature embedding of state-action pairs. To estimate such systems in finite time identification methods must explore all directions in feature space. We propose an active learning approach that achieves this by repeating three steps: trajectory planning, trajectory tracking, and re-estimation of the system from all available data. We show that our method estimates nonlinear dynamical systems at a parametric rate, similar to the statistical rate of standard linear regression.

Competing Bandits in Matching Markets

Stable matching, a classical model for two-sided markets, has long been studied with little consideration for how each side's preferences are learned. With the advent of massive online markets powered by data-driven matching platforms, it has become necessary to better understand the interplay between learning and market objectives. We propose a statistical learning model in which one side of the market does not have a priori knowledge about its preferences for the other side and is required to learn these from stochastic rewards. Our model extends the standard multi-armed bandits framework to multiple players, with the added feature that arms have preferences over players. We study both centralized and decentralized approaches to this problem and show surprising exploration-exploitation trade-offs compared to the single player multi-armed bandits setting.

Model Similarity Mitigates Test Set Overuse

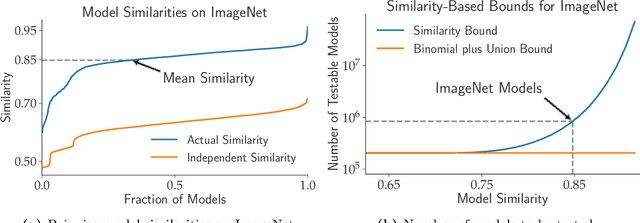
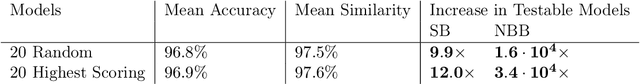
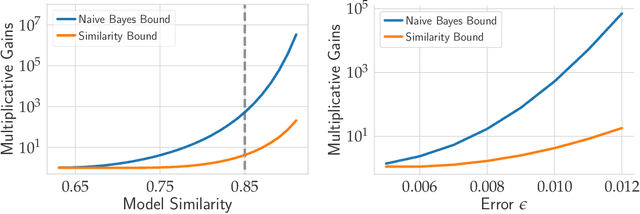
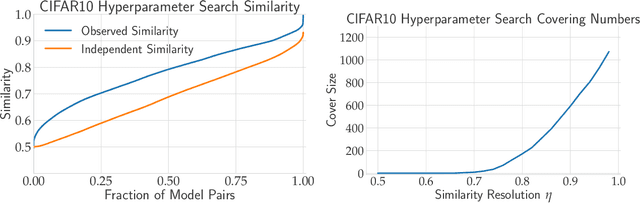
Excessive reuse of test data has become commonplace in today's machine learning workflows. Popular benchmarks, competitions, industrial scale tuning, among other applications, all involve test data reuse beyond guidance by statistical confidence bounds. Nonetheless, recent replication studies give evidence that popular benchmarks continue to support progress despite years of extensive reuse. We proffer a new explanation for the apparent longevity of test data: Many proposed models are similar in their predictions and we prove that this similarity mitigates overfitting. Specifically, we show empirically that models proposed for the ImageNet ILSVRC benchmark agree in their predictions well beyond what we can conclude from their accuracy levels alone. Likewise, models created by large scale hyperparameter search enjoy high levels of similarity. Motivated by these empirical observations, we give a non-asymptotic generalization bound that takes similarity into account, leading to meaningful confidence bounds in practical settings.

Certainty Equivalent Control of LQR is Efficient

We study the performance of the certainty equivalent controller on the Linear Quadratic Regulator (LQR) with unknown transition dynamics. We show that the sub-optimality gap between the cost incurred by playing the certainty equivalent controller on the true system and the cost incurred by using the optimal LQR controller enjoys a fast statistical rate, scaling as the square of the parameter error. Our result improves upon recent work by Dean et al. (2017), who present an algorithm achieving a sub-optimality gap linear in the parameter error. A key part of our analysis relies on perturbation bounds for discrete Riccati equations. We provide two new perturbation bounds, one that expands on an existing result from Konstantinov et al. (1993), and another based on a new elementary proof strategy. Our results show that certainty equivalent control with $\varepsilon$-greedy exploration achieves $\tilde{\mathcal{O}}(\sqrt{T})$ regret in the adaptive LQR setting, yielding the first guarantee of a computationally tractable algorithm that achieves nearly optimal regret for adaptive LQR.

Learning Without Mixing: Towards A Sharp Analysis of Linear System Identification

We prove that the ordinary least-squares (OLS) estimator attains nearly minimax optimal performance for the identification of linear dynamical systems from a single observed trajectory. Our upper bound relies on a generalization of Mendelson's small-ball method to dependent data, eschewing the use of standard mixing-time arguments. Our lower bounds reveal that these upper bounds match up to logarithmic factors. In particular, we capture the correct signal-to-noise behavior of the problem, showing that more unstable linear systems are easier to estimate. This behavior is qualitatively different from arguments which rely on mixing-time calculations that suggest that unstable systems are more difficult to estimate. We generalize our technique to provide bounds for a more general class of linear response time-series.

Regret Bounds for Robust Adaptive Control of the Linear Quadratic Regulator

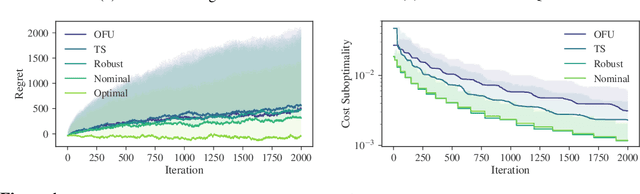
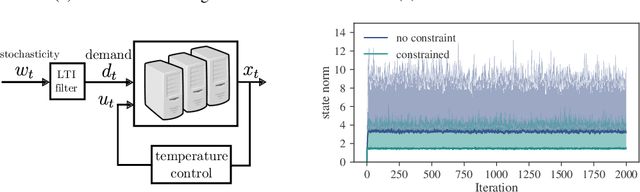
We consider adaptive control of the Linear Quadratic Regulator (LQR), where an unknown linear system is controlled subject to quadratic costs. Leveraging recent developments in the estimation of linear systems and in robust controller synthesis, we present the first provably polynomial time algorithm that provides high probability guarantees of sub-linear regret on this problem. We further study the interplay between regret minimization and parameter estimation by proving a lower bound on the expected regret in terms of the exploration schedule used by any algorithm. Finally, we conduct a numerical study comparing our robust adaptive algorithm to other methods from the adaptive LQR literature, and demonstrate the flexibility of our proposed method by extending it to a demand forecasting problem subject to state constraints.