Farhad Shirani
LM$^2$otifs : An Explainable Framework for Machine-Generated Texts Detection
May 18, 2025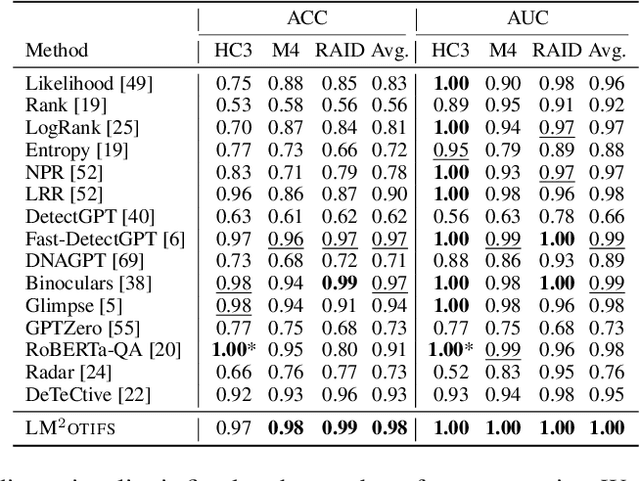
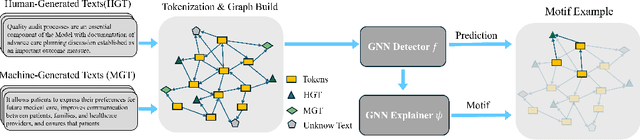
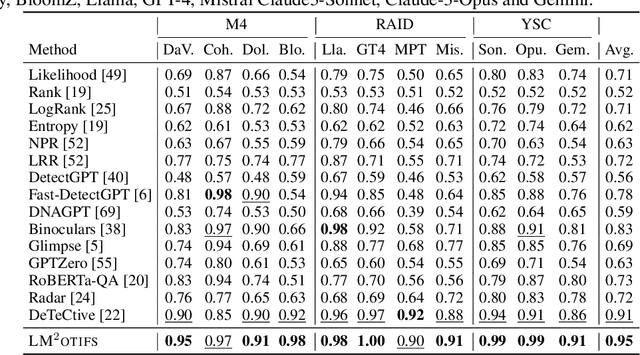
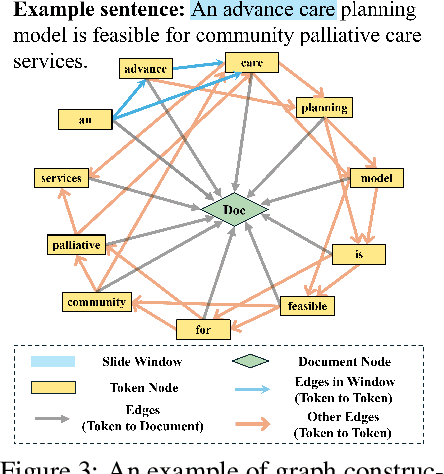
Abstract:The impressive ability of large language models to generate natural text across various tasks has led to critical challenges in authorship authentication. Although numerous detection methods have been developed to differentiate between machine-generated texts (MGT) and human-generated texts (HGT), the explainability of these methods remains a significant gap. Traditional explainability techniques often fall short in capturing the complex word relationships that distinguish HGT from MGT. To address this limitation, we present LM$^2$otifs, a novel explainable framework for MGT detection. Inspired by probabilistic graphical models, we provide a theoretical rationale for the effectiveness. LM$^2$otifs utilizes eXplainable Graph Neural Networks to achieve both accurate detection and interpretability. The LM$^2$otifs pipeline operates in three key stages: first, it transforms text into graphs based on word co-occurrence to represent lexical dependencies; second, graph neural networks are used for prediction; and third, a post-hoc explainability method extracts interpretable motifs, offering multi-level explanations from individual words to sentence structures. Extensive experiments on multiple benchmark datasets demonstrate the comparable performance of LM$^2$otifs. The empirical evaluation of the extracted explainable motifs confirms their effectiveness in differentiating HGT and MGT. Furthermore, qualitative analysis reveals distinct and visible linguistic fingerprints characteristic of MGT.
Explanation-Preserving Augmentation for Semi-Supervised Graph Representation Learning
Oct 16, 2024Abstract:Graph representation learning (GRL), enhanced by graph augmentation methods, has emerged as an effective technique achieving performance improvements in wide tasks such as node classification and graph classification. In self-supervised GRL, paired graph augmentations are generated from each graph. Its objective is to infer similar representations for augmentations of the same graph, but maximally distinguishable representations for augmentations of different graphs. Analogous to image and language domains, the desiderata of an ideal augmentation method include both (1) semantics-preservation; and (2) data-perturbation; i.e., an augmented graph should preserve the semantics of its original graph while carrying sufficient variance. However, most existing (un-)/self-supervised GRL methods focus on data perturbation but largely neglect semantics preservation. To address this challenge, in this paper, we propose a novel method, Explanation-Preserving Augmentation (EPA), that leverages graph explanation techniques for generating augmented graphs that can bridge the gap between semantics-preservation and data-perturbation. EPA first uses a small number of labels to train a graph explainer to infer the sub-structures (explanations) that are most relevant to a graph's semantics. These explanations are then used to generate semantics-preserving augmentations for self-supervised GRL, namely EPA-GRL. We demonstrate theoretically, using an analytical example, and through extensive experiments on a variety of benchmark datasets that EPA-GRL outperforms the state-of-the-art (SOTA) GRL methods, which are built upon semantics-agnostic data augmentations.
F-Fidelity: A Robust Framework for Faithfulness Evaluation of Explainable AI
Oct 03, 2024Abstract:Recent research has developed a number of eXplainable AI (XAI) techniques. Although extracting meaningful insights from deep learning models, how to properly evaluate these XAI methods remains an open problem. The most widely used approach is to perturb or even remove what the XAI method considers to be the most important features in an input and observe the changes in the output prediction. This approach although efficient suffers the Out-of-Distribution (OOD) problem as the perturbed samples may no longer follow the original data distribution. A recent method RemOve And Retrain (ROAR) solves the OOD issue by retraining the model with perturbed samples guided by explanations. However, the training may not always converge given the distribution difference. Furthermore, using the model retrained based on XAI methods to evaluate these explainers may cause information leakage and thus lead to unfair comparisons. We propose Fine-tuned Fidelity F-Fidelity, a robust evaluation framework for XAI, which utilizes i) an explanation-agnostic fine-tuning strategy, thus mitigating the information leakage issue and ii) a random masking operation that ensures that the removal step does not generate an OOD input. We designed controlled experiments with state-of-the-art (SOTA) explainers and their degraded version to verify the correctness of our framework. We conducted experiments on multiple data structures, such as images, time series, and natural language. The results demonstrate that F-Fidelity significantly improves upon prior evaluation metrics in recovering the ground-truth ranking of the explainers. Furthermore, we show both theoretically and empirically that, given a faithful explainer, F-Fidelity metric can be used to compute the sparsity of influential input components, i.e., to extract the true explanation size.
TimeX++: Learning Time-Series Explanations with Information Bottleneck
May 15, 2024Abstract:Explaining deep learning models operating on time series data is crucial in various applications of interest which require interpretable and transparent insights from time series signals. In this work, we investigate this problem from an information theoretic perspective and show that most existing measures of explainability may suffer from trivial solutions and distributional shift issues. To address these issues, we introduce a simple yet practical objective function for time series explainable learning. The design of the objective function builds upon the principle of information bottleneck (IB), and modifies the IB objective function to avoid trivial solutions and distributional shift issues. We further present TimeX++, a novel explanation framework that leverages a parametric network to produce explanation-embedded instances that are both in-distributed and label-preserving. We evaluate TimeX++ on both synthetic and real-world datasets comparing its performance against leading baselines, and validate its practical efficacy through case studies in a real-world environmental application. Quantitative and qualitative evaluations show that TimeX++ outperforms baselines across all datasets, demonstrating a substantial improvement in explanation quality for time series data. The source code is available at \url{https://github.com/zichuan-liu/TimeXplusplus}.
On Non-Interactive Simulation of Distributed Sources with Finite Alphabets
Mar 01, 2024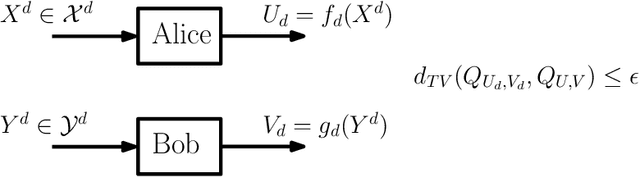
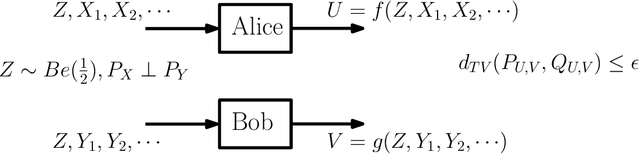
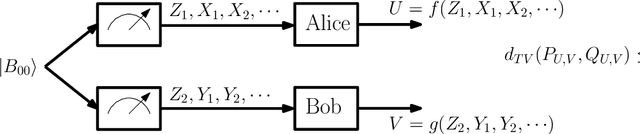

Abstract:This work presents a Fourier analysis framework for the non-interactive source simulation (NISS) problem. Two distributed agents observe a pair of sequences $X^d$ and $Y^d$ drawn according to a joint distribution $P_{X^dY^d}$. The agents aim to generate outputs $U=f_d(X^d)$ and $V=g_d(Y^d)$ with a joint distribution sufficiently close in total variation to a target distribution $Q_{UV}$. Existing works have shown that the NISS problem with finite-alphabet outputs is decidable. For the binary-output NISS, an upper-bound to the input complexity was derived which is $O(\exp\operatorname{poly}(\frac{1}{\epsilon}))$. In this work, the input complexity and algorithm design are addressed in several classes of NISS scenarios. For binary-output NISS scenarios with doubly-symmetric binary inputs, it is shown that the input complexity is $\Theta(\log{\frac{1}{\epsilon}})$, thus providing a super-exponential improvement in input complexity. An explicit characterization of the simulating pair of functions is provided. For general finite-input scenarios, a constructive algorithm is introduced that explicitly finds the simulating functions $(f_d(X^d),g_d(Y^d))$. The approach relies on a novel Fourier analysis framework. Various numerical simulations of NISS scenarios with IID inputs are provided. Furthermore, to illustrate the general applicability of the Fourier framework, several examples with non-IID inputs, including entanglement-assisted NISS and NISS with Markovian inputs are provided.
PAC Learnability under Explanation-Preserving Graph Perturbations
Feb 07, 2024
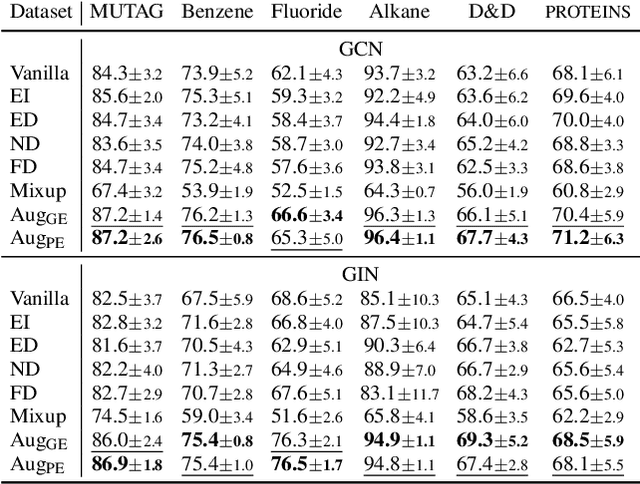

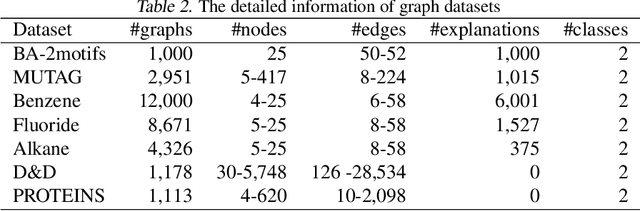
Abstract:Graphical models capture relations between entities in a wide range of applications including social networks, biology, and natural language processing, among others. Graph neural networks (GNN) are neural models that operate over graphs, enabling the model to leverage the complex relationships and dependencies in graph-structured data. A graph explanation is a subgraph which is an `almost sufficient' statistic of the input graph with respect to its classification label. Consequently, the classification label is invariant, with high probability, to perturbations of graph edges not belonging to its explanation subgraph. This work considers two methods for leveraging such perturbation invariances in the design and training of GNNs. First, explanation-assisted learning rules are considered. It is shown that the sample complexity of explanation-assisted learning can be arbitrarily smaller than explanation-agnostic learning. Next, explanation-assisted data augmentation is considered, where the training set is enlarged by artificially producing new training samples via perturbation of the non-explanation edges in the original training set. It is shown that such data augmentation methods may improve performance if the augmented data is in-distribution, however, it may also lead to worse sample complexity compared to explanation-agnostic learning rules if the augmented data is out-of-distribution. Extensive empirical evaluations are provided to verify the theoretical analysis.
Non-Linear Analog Processing Gains in Task-Based Quantization
Feb 02, 2024Abstract:In task-based quantization, a multivariate analog signal is transformed into a digital signal using a limited number of low-resolution analog-to-digital converters (ADCs). This process aims to minimize a fidelity criterion, which is assessed against an unobserved task variable that is correlated with the analog signal. The scenario models various applications of interest such as channel estimation, medical imaging applications, and object localization. This work explores the integration of analog processing components -- such as analog delay elements, polynomial operators, and envelope detectors -- prior to ADC quantization. Specifically, four scenarios, involving different collections of analog processing operators are considered: (i) arbitrary polynomial operators with analog delay elements, (ii) limited-degree polynomial operators, excluding delay elements, (iii) sequences of envelope detectors, and (iv) a combination of analog delay elements and linear combiners. For each scenario, the minimum achievable distortion is quantified through derivation of computable expressions in various statistical settings. It is shown that analog processing can significantly reduce the distortion in task reconstruction. Numerical simulations in a Gaussian example are provided to give further insights into the aforementioned analog processing gains.
Factorized Explainer for Graph Neural Networks
Dec 09, 2023



Abstract:Graph Neural Networks (GNNs) have received increasing attention due to their ability to learn from graph-structured data. To open the black-box of these deep learning models, post-hoc instance-level explanation methods have been proposed to understand GNN predictions. These methods seek to discover substructures that explain the prediction behavior of a trained GNN. In this paper, we show analytically that for a large class of explanation tasks, conventional approaches, which are based on the principle of graph information bottleneck (GIB), admit trivial solutions that do not align with the notion of explainability. Instead, we argue that a modified GIB principle may be used to avoid the aforementioned trivial solutions. We further introduce a novel factorized explanation model with theoretical performance guarantees. The modified GIB is used to analyze the structural properties of the proposed factorized explainer. We conduct extensive experiments on both synthetic and real-world datasets to validate the effectiveness of our proposed factorized explainer over existing approaches.
Towards Robust Fidelity for Evaluating Explainability of Graph Neural Networks
Oct 03, 2023Abstract:Graph Neural Networks (GNNs) are neural models that leverage the dependency structure in graphical data via message passing among the graph nodes. GNNs have emerged as pivotal architectures in analyzing graph-structured data, and their expansive application in sensitive domains requires a comprehensive understanding of their decision-making processes -- necessitating a framework for GNN explainability. An explanation function for GNNs takes a pre-trained GNN along with a graph as input, to produce a `sufficient statistic' subgraph with respect to the graph label. A main challenge in studying GNN explainability is to provide fidelity measures that evaluate the performance of these explanation functions. This paper studies this foundational challenge, spotlighting the inherent limitations of prevailing fidelity metrics, including $Fid_+$, $Fid_-$, and $Fid_\Delta$. Specifically, a formal, information-theoretic definition of explainability is introduced and it is shown that existing metrics often fail to align with this definition across various statistical scenarios. The reason is due to potential distribution shifts when subgraphs are removed in computing these fidelity measures. Subsequently, a robust class of fidelity measures are introduced, and it is shown analytically that they are resilient to distribution shift issues and are applicable in a wide range of scenarios. Extensive empirical analysis on both synthetic and real datasets are provided to illustrate that the proposed metrics are more coherent with gold standard metrics.
Capacity Gains in MIMO Systems with Few-Bit ADCs Using Nonlinear Analog Operators
Dec 12, 2022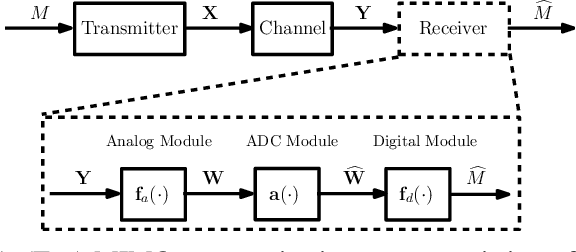

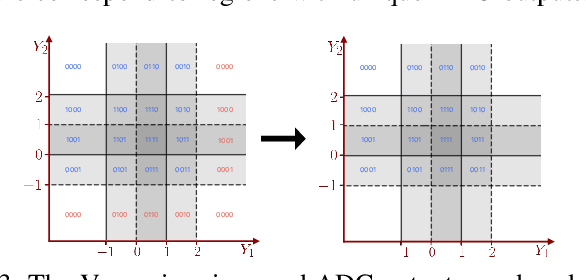
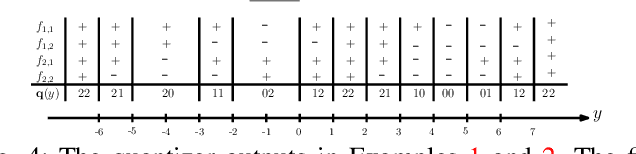
Abstract:Analog to Digital Converters (ADCs) are a major contributor to the power consumption of multiple-input multiple-output (MIMO) receivers with large antenna arrays operating in the millimeter wave and terahertz carrier frequencies. This is especially the case in large bandwidth terahertz communication systems, due to the sudden drop in energy-efficiency of ADCs as the sampling rate is increased above 100MHz. Two mitigating energy-efficient approaches which have received significant recent interest are i) to reduce the number of ADCs via analog and hybrid beamforming architectures, and ii) to reduce the resolution of the ADCs which in turn decreases power consumption. However, decreasing the number and resolution of ADCs leads to performance loss -- in terms of achievable rates -- due to increased quantization error. In this work, we study the application of practically implementable nonlinear analog operators such as envelop detectors and polynomial operators, prior to sampling and quantization at the ADCs, as a way to mitigate the aforementioned rate-loss. A receiver architecture consisting of linear analog combiners, nonlinear analog operators, and few-bit ADCs is designed. The fundamental information theoretic performance limits of the resulting communication system, in terms of achievable rates, are investigated under various assumptions on the set of implementable analog operators. Various numerical evaluations and simulations of the communication system are provided to compare the set of achievable rates under different architecture designs and parameters. Circuit simulations {in a 65 nm CMOS technology} exhibiting the generation of envelope detectors and polynomial operators are provided, and their power consumption is compared.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge