TimeX++: Learning Time-Series Explanations with Information Bottleneck

Explaining deep learning models operating on time series data is crucial in various applications of interest which require interpretable and transparent insights from time series signals. In this work, we investigate this problem from an information theoretic perspective and show that most existing measures of explainability may suffer from trivial solutions and distributional shift issues. To address these issues, we introduce a simple yet practical objective function for time series explainable learning. The design of the objective function builds upon the principle of information bottleneck (IB), and modifies the IB objective function to avoid trivial solutions and distributional shift issues. We further present TimeX++, a novel explanation framework that leverages a parametric network to produce explanation-embedded instances that are both in-distributed and label-preserving. We evaluate TimeX++ on both synthetic and real-world datasets comparing its performance against leading baselines, and validate its practical efficacy through case studies in a real-world environmental application. Quantitative and qualitative evaluations show that TimeX++ outperforms baselines across all datasets, demonstrating a substantial improvement in explanation quality for time series data. The source code is available at \url{https://github.com/zichuan-liu/TimeXplusplus}.

PAC Learnability under Explanation-Preserving Graph Perturbations

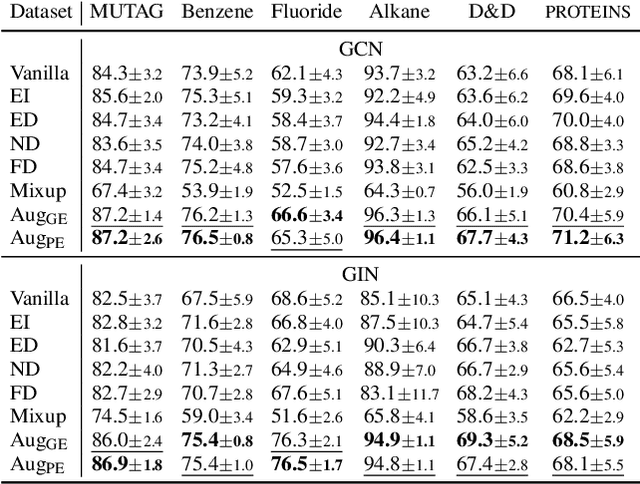
Graphical models capture relations between entities in a wide range of applications including social networks, biology, and natural language processing, among others. Graph neural networks (GNN) are neural models that operate over graphs, enabling the model to leverage the complex relationships and dependencies in graph-structured data. A graph explanation is a subgraph which is an `almost sufficient' statistic of the input graph with respect to its classification label. Consequently, the classification label is invariant, with high probability, to perturbations of graph edges not belonging to its explanation subgraph. This work considers two methods for leveraging such perturbation invariances in the design and training of GNNs. First, explanation-assisted learning rules are considered. It is shown that the sample complexity of explanation-assisted learning can be arbitrarily smaller than explanation-agnostic learning. Next, explanation-assisted data augmentation is considered, where the training set is enlarged by artificially producing new training samples via perturbation of the non-explanation edges in the original training set. It is shown that such data augmentation methods may improve performance if the augmented data is in-distribution, however, it may also lead to worse sample complexity compared to explanation-agnostic learning rules if the augmented data is out-of-distribution. Extensive empirical evaluations are provided to verify the theoretical analysis.

CMFDFormer: Transformer-based Copy-Move Forgery Detection with Continual Learning

Copy-move forgery detection aims at detecting duplicated regions in a suspected forged image, and deep learning based copy-move forgery detection methods are in the ascendant. These deep learning based methods heavily rely on synthetic training data, and the performance will degrade when facing new tasks. In this paper, we propose a Transformer-style copy-move forgery detection network named as CMFDFormer, and provide a novel PCSD (Pooled Cube and Strip Distillation) continual learning framework to help CMFDFormer handle new tasks. CMFDFormer consists of a MiT (Mix Transformer) backbone network and a PHD (Pluggable Hybrid Decoder) mask prediction network. The MiT backbone network is a Transformer-style network which is adopted on the basis of comprehensive analyses with CNN-style and MLP-style backbones. The PHD network is constructed based on self-correlation computation, hierarchical feature integration, a multi-scale cycle fully-connected block and a mask reconstruction block. The PHD network is applicable to feature extractors of different styles for hierarchical multi-scale information extraction, achieving comparable performance. Last but not least, we propose a PCSD continual learning framework to improve the forgery detectability and avoid catastrophic forgetting when handling new tasks. Our continual learning framework restricts intermediate features from the PHD network, and takes advantage of both cube pooling and strip pooling. Extensive experiments on publicly available datasets demonstrate the good performance of CMFDFormer and the effectiveness of the PCSD continual learning framework.

HurriCast: An Automatic Framework Using Machine Learning and Statistical Modeling for Hurricane Forecasting

Hurricanes present major challenges in the U.S. due to their devastating impacts. Mitigating these risks is important, and the insurance industry is central in this effort, using intricate statistical models for risk assessment. However, these models often neglect key temporal and spatial hurricane patterns and are limited by data scarcity. This study introduces a refined approach combining the ARIMA model and K-MEANS to better capture hurricane trends, and an Autoencoder for enhanced hurricane simulations. Our experiments show that this hybrid methodology effectively simulate historical hurricane behaviors while providing detailed projections of potential future trajectories and intensities. Moreover, by leveraging a comprehensive yet selective dataset, our simulations enrich the current understanding of hurricane patterns and offer actionable insights for risk management strategies.

Adaptive Neural Network-Based Approximation to Accelerate Eulerian Fluid Simulation

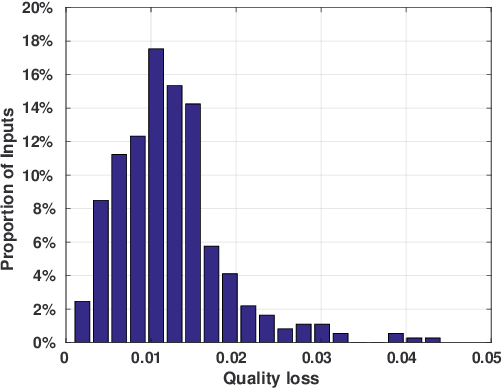
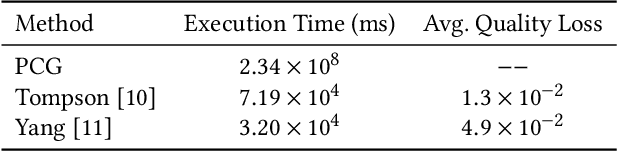
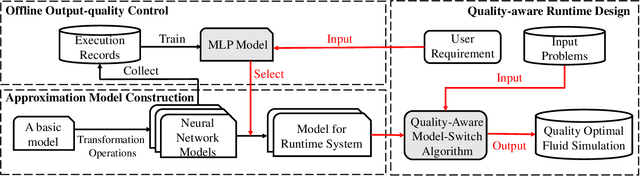
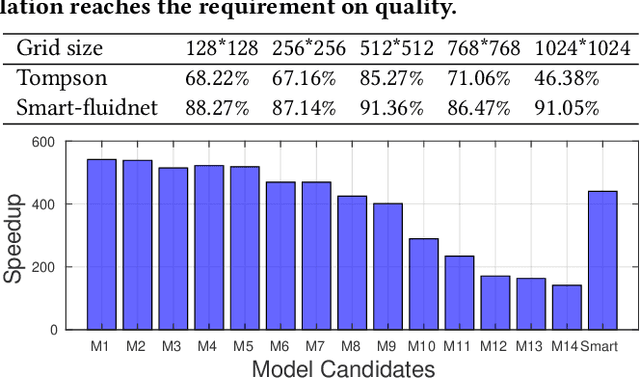
The Eulerian fluid simulation is an important HPC application. The neural network has been applied to accelerate it. The current methods that accelerate the fluid simulation with neural networks lack flexibility and generalization. In this paper, we tackle the above limitation and aim to enhance the applicability of neural networks in the Eulerian fluid simulation. We introduce Smartfluidnet, a framework that automates model generation and application. Given an existing neural network as input, Smartfluidnet generates multiple neural networks before the simulation to meet the execution time and simulation quality requirement. During the simulation, Smartfluidnet dynamically switches the neural networks to make the best efforts to reach the user requirement on simulation quality. Evaluating with 20,480 input problems, we show that Smartfluidnet achieves 1.46x and 590x speedup comparing with a state-of-the-art neural network model and the original fluid simulation respectively on an NVIDIA Titan X Pascal GPU, while providing better simulation quality than the state-of-the-art model.

Smart-PGSim: Using Neural Network to Accelerate AC-OPF Power Grid Simulation

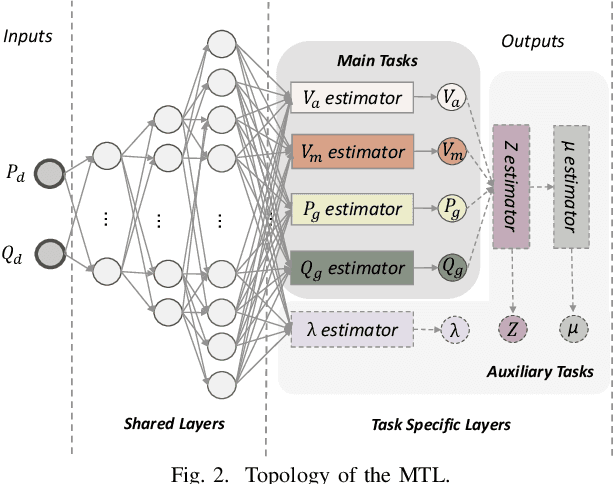
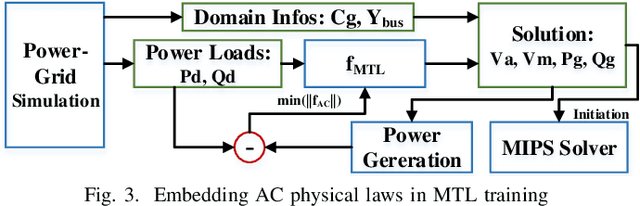
The optimal power flow (OPF) problem is one of the most important optimization problems for the operation of the power grid. It calculates the optimum scheduling of the committed generation units. In this paper, we develop a neural network approach to the problem of accelerating the current optimal power flow (AC-OPF) by generating an intelligent initial solution. The high quality of the initial solution and guidance of other outputs generated by the neural network enables faster convergence to the solution without losing optimality of final solution as computed by traditional methods. Smart-PGSim generates a novel multitask-learning neural network model to accelerate the AC-OPF simulation. Smart-PGSim also imposes the physical constraints of the simulation on the neural network automatically. Smart-PGSim brings an average of 49.2% performance improvement (up to 91%), computed over 10,000 problem simulations, with respect to the original AC-OPF implementation, without losing the optimality of the final solution.

A Preliminary Study of Neural Network-based Approximation for HPC Applications

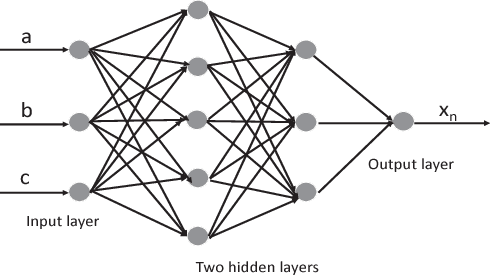
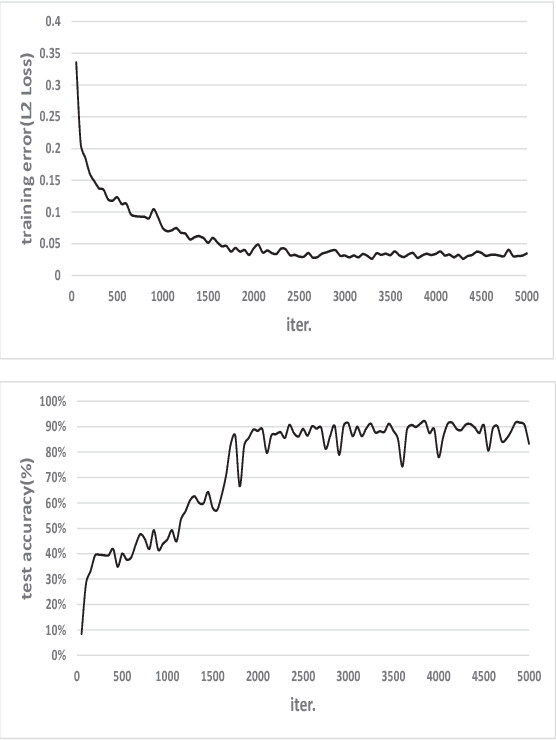
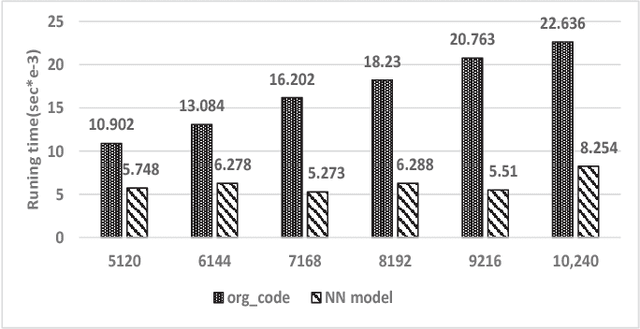
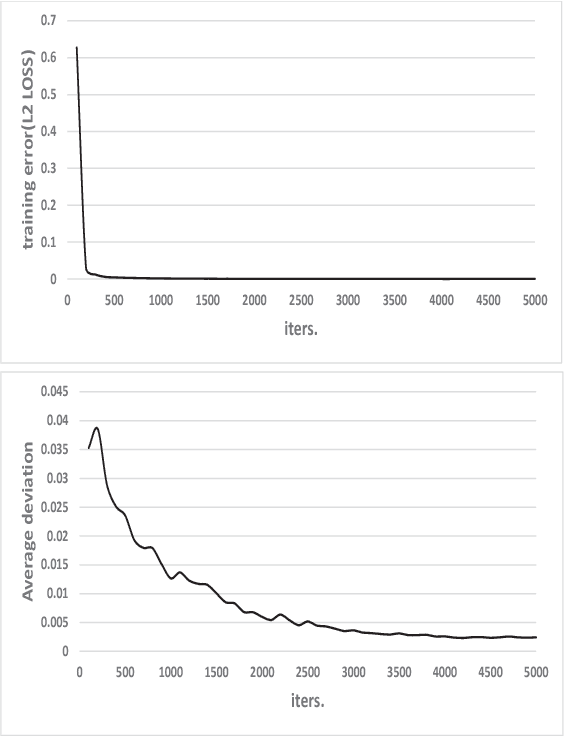
Machine learning, as a tool to learn and model complicated (non)linear relationships between input and output data sets, has shown preliminary success in some HPC problems. Using machine learning, scientists are able to augment existing simulations by improving accuracy and significantly reducing latencies. Our ongoing research work is to create a general framework to apply neural network-based models to HPC applications. In particular, we want to use the neural network to approximate and replace code regions within the HPC application to improve performance (i.e., reducing the execution time) of the HPC application. In this paper, we present our preliminary study and results. Using two applications (the Newton-Raphson method and the Lennard-Jones (LJ) potential in LAMMP) for our case study, we achieve up to 2.7x and 2.46x speedup, respectively.