PAC Learnability under Explanation-Preserving Graph Perturbations
Paper and Code
Feb 07, 2024
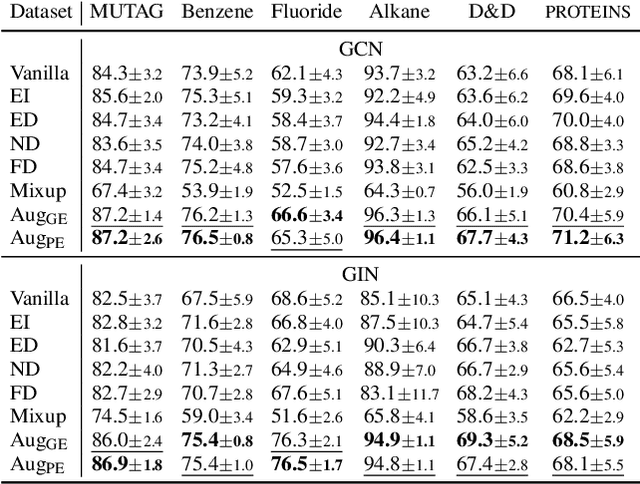

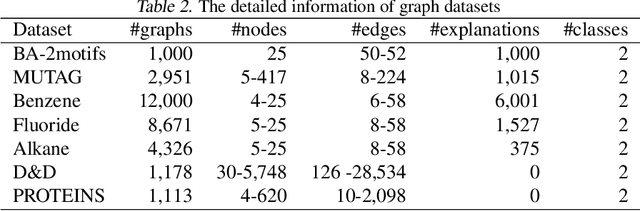
Graphical models capture relations between entities in a wide range of applications including social networks, biology, and natural language processing, among others. Graph neural networks (GNN) are neural models that operate over graphs, enabling the model to leverage the complex relationships and dependencies in graph-structured data. A graph explanation is a subgraph which is an `almost sufficient' statistic of the input graph with respect to its classification label. Consequently, the classification label is invariant, with high probability, to perturbations of graph edges not belonging to its explanation subgraph. This work considers two methods for leveraging such perturbation invariances in the design and training of GNNs. First, explanation-assisted learning rules are considered. It is shown that the sample complexity of explanation-assisted learning can be arbitrarily smaller than explanation-agnostic learning. Next, explanation-assisted data augmentation is considered, where the training set is enlarged by artificially producing new training samples via perturbation of the non-explanation edges in the original training set. It is shown that such data augmentation methods may improve performance if the augmented data is in-distribution, however, it may also lead to worse sample complexity compared to explanation-agnostic learning rules if the augmented data is out-of-distribution. Extensive empirical evaluations are provided to verify the theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge