Non-Linear Analog Processing Gains in Task-Based Quantization

In task-based quantization, a multivariate analog signal is transformed into a digital signal using a limited number of low-resolution analog-to-digital converters (ADCs). This process aims to minimize a fidelity criterion, which is assessed against an unobserved task variable that is correlated with the analog signal. The scenario models various applications of interest such as channel estimation, medical imaging applications, and object localization. This work explores the integration of analog processing components -- such as analog delay elements, polynomial operators, and envelope detectors -- prior to ADC quantization. Specifically, four scenarios, involving different collections of analog processing operators are considered: (i) arbitrary polynomial operators with analog delay elements, (ii) limited-degree polynomial operators, excluding delay elements, (iii) sequences of envelope detectors, and (iv) a combination of analog delay elements and linear combiners. For each scenario, the minimum achievable distortion is quantified through derivation of computable expressions in various statistical settings. It is shown that analog processing can significantly reduce the distortion in task reconstruction. Numerical simulations in a Gaussian example are provided to give further insights into the aforementioned analog processing gains.

Capacity Gains in MIMO Systems with Few-Bit ADCs Using Nonlinear Analog Operators

Analog to Digital Converters (ADCs) are a major contributor to the power consumption of multiple-input multiple-output (MIMO) receivers with large antenna arrays operating in the millimeter wave and terahertz carrier frequencies. This is especially the case in large bandwidth terahertz communication systems, due to the sudden drop in energy-efficiency of ADCs as the sampling rate is increased above 100MHz. Two mitigating energy-efficient approaches which have received significant recent interest are i) to reduce the number of ADCs via analog and hybrid beamforming architectures, and ii) to reduce the resolution of the ADCs which in turn decreases power consumption. However, decreasing the number and resolution of ADCs leads to performance loss -- in terms of achievable rates -- due to increased quantization error. In this work, we study the application of practically implementable nonlinear analog operators such as envelop detectors and polynomial operators, prior to sampling and quantization at the ADCs, as a way to mitigate the aforementioned rate-loss. A receiver architecture consisting of linear analog combiners, nonlinear analog operators, and few-bit ADCs is designed. The fundamental information theoretic performance limits of the resulting communication system, in terms of achievable rates, are investigated under various assumptions on the set of implementable analog operators. Various numerical evaluations and simulations of the communication system are provided to compare the set of achievable rates under different architecture designs and parameters. Circuit simulations {in a 65 nm CMOS technology} exhibiting the generation of envelope detectors and polynomial operators are provided, and their power consumption is compared.

Optimal Distributed Fault-Tolerant Sensor Fusion: Fundamental Limits and Efficient Algorithms

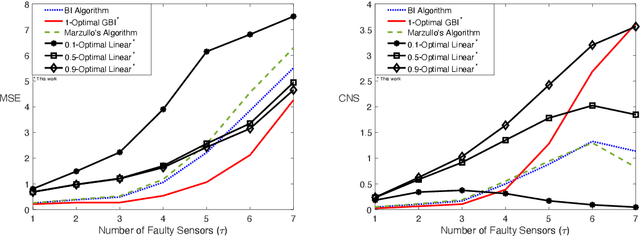
Distributed estimation is a fundamental problem in signal processing which finds applications in a variety of scenarios of interest including distributed sensor networks, robotics, group decision problems, and monitoring and surveillance applications. The problem considers a scenario where distributed agents are given a set of measurements, and are tasked with estimating a target variable. This work considers distributed estimation in the context of sensor networks, where a subset of sensor measurements are faulty and the distributed agents are agnostic to these faulty sensor measurements. The objective is to minimize i) the mean square error in estimating the target variable at each node (accuracy objective), and ii) the mean square distance between the estimates at each pair of nodes (consensus objective). It is shown that there is an inherent tradeoff between satisfying the former and latter objectives. The tradeoff is explicitly characterized and the fundamental performance limits are derived under specific statistical assumptions on the sensor output statistics. Assuming a general stochastic model, the sensor fusion algorithm optimizing this tradeoff is characterized through a computable optimization problem. Finding the optimal sensor fusion algorithm is computationally complex. To address this, a general class of low-complexity Brooks-Iyengar Algorithms are introduced, and their performance, in terms of accuracy and consensus objectives, is compared to that of optimal linear estimators through case study simulations of various scenarios.